Linear programming problem - Mathematical formulation of a linear programming problem | 11th Business Mathematics and Statistics(EMS) : Chapter 10 : Operations Research
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 10 : Operations Research
Mathematical formulation of a linear programming problem
Mathematical
formulation of a linear programming problem:
The procedure for mathematical formulation of a linear programming problem consists of the following steps.
(i) Identify
the decision variables.
(ii) Identify
the objective function to be maximized or minimized and express it as a
linear function of decision variables.
(iii) Identify
the set of constraint conditions and express them as linear inequalities or
equations in terms of the decision variables.
Example 10.1
A
furniture dealer deals only two items viz., tables and chairs. He has to invest
Rs.10,000/- and a space to store atmost 60 pieces. A table cost him Rs.500/–
and a chair Rs.200/–. He can sell all the items that he buys. He is getting a
profit of Rs.50 per table and Rs.15 per chair. Formulate this problem as an
LPP, so as to maximize the profit.
Solution:
(i) Variables: Let x1 and x2 denote the number of tables and chairs
respectively.
(i) Objective function:
Profit on
x1 tables = 50 x1
Profit on
x2 chairs = 15 x2
Total
profit = 50 x1+15x2
Let Z = 50 x1+15 x2
, which is the objective function.
Since the total profit is to be
maximized, we have to maximize Z=50x1+15x2
(iii) Constraints:
The dealer has a space to store
atmost 60 pieces
x1+x2 ≤ 60
The cost of x1 tables = Rs.500 x1
The cost of x2 tables = Rs. 200 x2
Total cost = 500 x1 + 200 x2 ,which cannot be more than 10000
500 x1 + 200 x2
≤ 10000
5x1+ 2x2 ≤ 100
(iv) Non-negative restrictions: Since the
number of tables and chairs cannot be negative,
we have x1 ≥0, x2 ≥0
Thus, the mathematical
formulation of the LPP is
Maximize Z=50 x1+15x2
Subject to the constrains
x1+x2 ≤60
5x1+2x2≤100
x1, x2≥0
Example 10.2
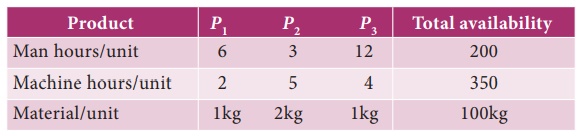
A company
is producing three products P1,
P2 and P3, with profit contribution
of Rs.20,Rs.25 and Rs.15 per unit respectively. The resource requirements per
unit of each of the products and total availability are given below.
Formulate
the above as a linear programming model.
Solution:
(i) Variables: Let x1 ,
x2 and x3 be the number of units of products P1, P2 and P3 to
be produced.
(ii) Objective function: Profit on x1 units of the product P1 = 20 x1
Profit on x2 units of the product P2 = 25 x2
Profit on x3 units of the product P3 = 15 x3
Total profit = 20 x1 +25 x2 +15 x3
Since the total profit is to be
maximized, we have to maximize Z= 20 x1+25 x2 +15 x3
Constraints:
6x1 +3 x2 +12 x3
≤ 200
2 x1 +5 x2
+4 x3 ≤ 350
x1 +2 x2 + x3 ≤ 100
Non-negative restrictions: Since
the number of units of the products A,B and C cannot be negative, we have x1, x2, x3 ≥ 0
Thus, we have the following
linear programming model.
Maximize Z = 20 x1 +25 x2 +15 x3
Subject
to
6 x1 +3 x2 +12 x3≤
200
2x1+5x2
+4 x3 ≤ 350
x1+2 x2 + x3≤ 100
x1, x2, x3 ≥ 0
Example 10.3
A
dietician wishes to mix two types of food F1 and F2 in
such a way that the vitamin contents of the mixture contains atleast 6units of
vitamin A and 9 units of vitamin B. Food F1 costs Rs.50 per kg and F2
costs Rs 70 per kg. Food F1 contains 4 units per kg of vitamin A and
6 units per kg of vitamin B while food F2 contains 5 units per kg of
vitamin A and 3 units per kg of vitamin B. Formulate the above problem as a
linear programming problem to minimize the cost of mixture.
Solution:
(i) Variables: Let the mixture contains x1 kg of food F1 and x2 kg of food F2
(ii) Objective function:
cost of x1 kg of food F1 =
50 x1
cost of x2 kg of food F2 = 70x2
The cost is to be minimized
Therefore minimize Z= 50 x1+70x2
(iii)
Constraints:
We make
the following table from the given data
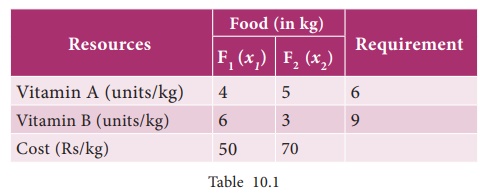
4x1+5x2 ≥6 (since the mixture contains ‘atleast 6’ units of vitamin A ,we
have the inequality of the type ≥ )
6x1+3x2 ≥9(since the mixture contains ‘atleast 9’ units of vitamin B ,we
have the inequality of the type ≥ )
(iv) Non-negative restrictions:
Since the number of kgs of
vitamin A and vitamin B are non-negative , we have x1, x2 ≥0
Thus, we
have the following linear programming model
Minimize
Z = 50 x1 +70x2
subject
to 4 x1+5x2 ≥6
6 x1+3x2 ≥9
and x1, x2≥0
Example 10.4
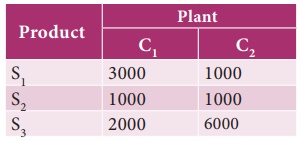
A soft
drink company has two bottling plants C1
and C2. Each plant
produces three different soft drinks S1,S2 and S3.
The production of the two plants in number of bottles per day are:
A market
survey indicates that during the month of April there will be a demand for
24000 bottles of S1, 16000 bottles of S2 and 48000
bottles of S3. The operating costs, per day, of running plants C1
and C2 are respectively Rs.600 and Rs.400. How many days should the
firm run each plant in April so that the production cost is minimized while
still meeting the market demand? Formulate the above as a linear programming
model.
Solution:
(i) Variables: Let x1
be the number of days required to run plant C1 and x2 be
the number of days required to run plant C2
Objective
function: Minimize Z = 600 x1 + 400 x2
(ii) Constraints: 3000 x1 + 1000 x2 ≥ 24000(since there is a demand of 24000 bottles of drink A, production should
not be less than 24000)
1000x1 + 1000 x2 ≥ 16000
2000x1+ 6000 x2 ≥ 48000
(iii) Non-negative restrictions: Since be the
number of days required of a firm are non-negative,
we have x1, x2 ≥0
Thus we
have the following LP model.
Minimize
Z = 600 x1 + 400 x2
subject
to 3000 x1 + 1000 x2 ≥ 24000
1000 x1 + 1000 x2 ≥ 16000
2000 x1 + 6000 x2 ≥ 48000
and x1, x2 ≥0
Related Topics