Linear programming problem

Linear programming problem

The Russian Mathematician L.V. Kantorovich applied mathematical model to solve linear programming problems. He pointed out in 1939 that many classes of problems which arise in production can be defined mathematically and therefore can be solved numerically. This decision making technique was further developed by George B. Dantziz. He formulated the general linear programming problem and developed simplex method (1947) to solve complex real time applications. Linear programming is one of the best optimization technique from theory, application and computation point of view.

Definition:

Linear Programming Problem(LPP) is a mathematical technique which is used to optimize (maximize or minimize) the objective function with the limited resources.

Mathematically, the general linear programming problem (LPP) may be stated as follows.

Maximize or Minimize Z = c₁ x₁ + c₂ x₂ + … + c_n x_n

Subject to the conditions (constraints)

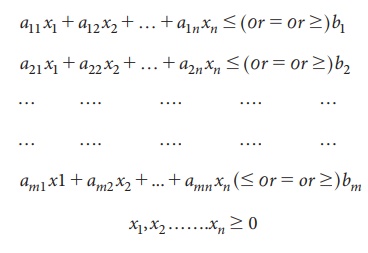
Short form of LPP

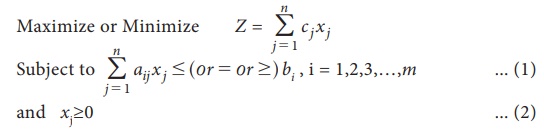
Some useful definitions:

Objective function:

A function Z=c₁ x₁ + c₂x₂ + …+ c_nx_n which is to be optimized (maximized or minimized) is called objective function.

Decision variable:

The decision variables are the variables, which has to be determined x_j , j = 1,2,3,…,n, to optimize the objective function.

Constraints:

There are certain limitations on the use of limited resources called constraints.

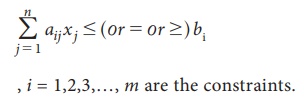
Solution:

A set of values of decision variables x_j, j=1,2,3,…, n satisfying all the constraints of the problem is called a solution to that problem.

Feasible solution:

A set of values of the decision variables that satisfies all the constraints of the problem and non-negativity restrictions is called a feasible solution of the problem.

Optimal solution:

Any feasible solution which maximizes or minimizes the objective function is called an optimal solution.

Feasible region:

The common region determined by all the constraints including non-negative constraints x_j ≥0 of a linear programming problem is called the feasible region (or solution region) for the problem.