Chapter: Digital Signal Processing : FIR Filter Design
Roundoff Noise in FIR Filters
Roundoff Noise in FIR Filters:
The simplest case to analyze is a finite impulse response (FIR) filter realized via the convolution summation
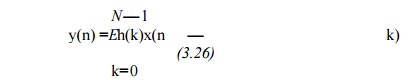
When fixed- point arithmetic is used and quantization is performed after each multiply, the result of the N multiplies isN-times the quantization noise of a single multiply. For example, rounding after each multiply gives, from (3.6) and (3.12), an output noise variance of

Virtually all digital signal processor integrated circuits contain one or more double-length accumulator registers which permit the sum-of-products in (3.26) to be accumulated without quantization. In this case only a single quantization is necessary following the summation and For the floating-point roundoff noise case we will consider (3.26) for N = 4 and then generalize the result to other values of N. The finite-precision output can be written as the exact output plus an error term e(n). Thus,
y(n) + e(n) = ({[h(0)x(n)[1 + E1(n)] + h(1)x(n -1)[1 + £2(n)]][1 + S3(n)] + h(2)x(n -2)[1 + £4(n)]}{1 + s5(n)} + h(3)x(n - 3)[1 + £6(n)])[1 + £j(n)] (3.29)
In (3.29), £1(n) represents the error in the first product, £2(n) the
error in the second product, £3(n) the error in the firstaddition, etc.Notice that it has been assumed that the products are summed in the order implied by the summation of (3.26).
Expanding (3.29), ignoring products of error terms, and recognizing y(n) gives
e(n) = h(0)x(n)[£1 (n) + £3(n) + £$(n) + £i(n)] + h(1)x(n-1)[£2(n) + £3(n) + £5(n) ++ h(2)x(n-2)[£4(n) + £5(n) + £i(n)] £j(n)] + h(3)x(n- 3)[£6(n)+ £j(n)]
(3.30)
Assuming that the input is white noise of variance a^ so that E{x(n)x(n - k)} is zero for k = 0, and assuming that the errors are uncorrelated
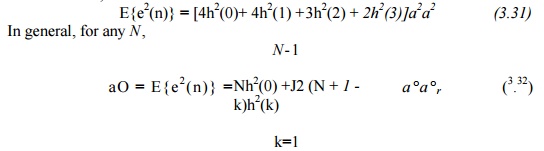
Notice that if the order of summation of the product terms in the convolution summation is changed, then the order in which the h(k)’s appear in (3.32) changes. If the order is changed so that the h(k)with smallest magnitude is first, followed by the next smallest, etc., then the roundoff noise variance is minimized. However, performing the convolution summation in nonsequential order greatly complicates data indexing and so may not be worth the reduction obtained in roundoff noise.
Roundoff Noise in Fixed-Point IIR Filters
To determine the roundoff noise of a fixed-point infinite impulse response (IIR) filter realization, consider a causal first-order filter with impulse response
h(n) = anu(n) (3.33)
realized by the difference equation
y(n) = ay(n - 1) + x(n) (3.34)
Due to roundoff error, the output actually obtained is
y(n) = Q{ay(n - 1) + x(n)} = ay(n - 1) + x(n) + e(n) (3.35)
where e(n) is a random roundoff noise sequence. Since e(n) is injected at the same point as the input, it propagates througha system with impulse response h(n).
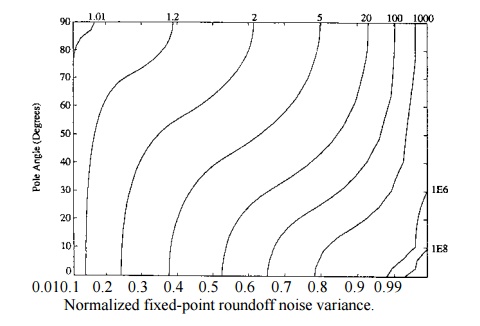
It is possible to design state-space filter realizations that minimize fixed-point roundoff noise [7] - [10]. Depending on the transfer function being realized, these structures may provide a roundoff noise level that is orders-of-magnitude lower than for a nonoptimal realization. The price paid for this reduction in roundoff noise is an increase in the number of computations required to implement the filter. For an Nth-order filter the increase is from roughly 2N multiplies for a direct form realization to roughly (N + 1)2 for an optimal realization. However, if the filter is realized by the parallel or cascade connection of first- and second-order optimal subfilters, the increase is only to about 4N multiplies. Furthermore, near-optimal realizations exist that increase the number of multiplies to only about 3N .
Related Topics