Digital Resonator

DIGITAL RESONATOR

A digital resonator is a special two pole bandpass filter with a pair of complex conjugate poles located near the unit circle. The name resonator refers to the fact that the filter has a larger magnitude response in the vicinity of the pole locations. Digital resonators are useful in many applications, including simple bandpass filtering and speech generations.

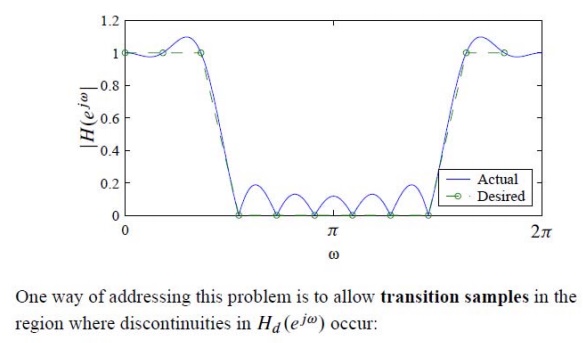
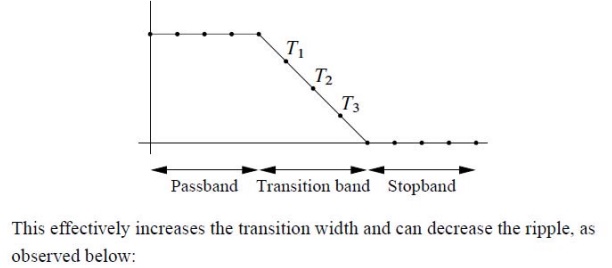
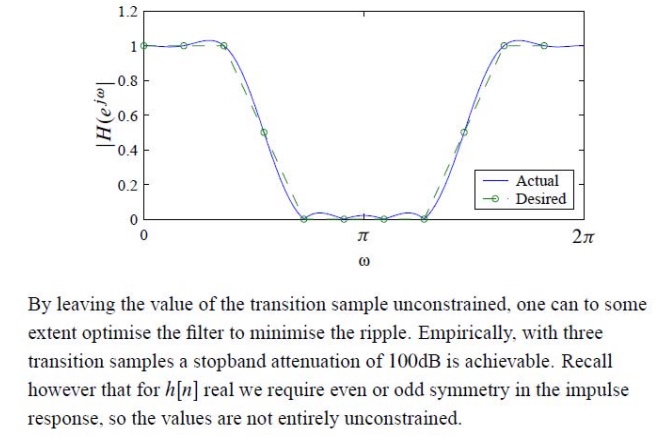
IDEAL FILTERS ARE NOT PHYSICALLY REALIZABLE. Why?

Ideal filters are not physically realizable because Ideal filters are anti-causal and as only causal systems are physically realizable.

Proof:

Let take example of ideal lowpass filter.

H(ω) = 1 for - ωc ≤ ω ≤ ωc

         = 0 elsewhere

The unit sample response of this ideal LPF can be obtained by taking IFT of H(ω).

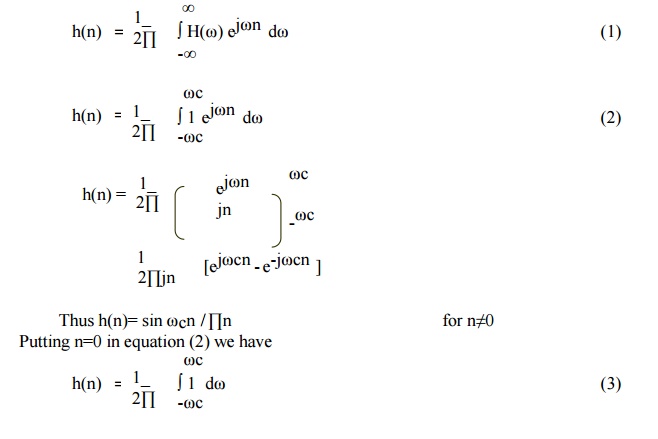
LSI system is causal if its unit sample response satisfies following condition. h(n) = 0

for n<0

In above figure h(n) extends -∞ to ∞ . Hence h(n) ≠0 for n<0. This means causality condition is not satisfied by the ideal low pass filter. Hence ideal low pass filter is non causal and it is not physically realizable.

EXAMPLES OF SIMPLE DIGITAL FILTERS:

The following examples illustrate the essential features of digital filters.

1. UNITY GAIN FILTER: y_n = x_n

Each output value y_n is exactly the same as the corresponding input value x_n:

2. SIMPLE GAIN FILTER: y_n = Kx_n (K = constant) Amplifier or attenuator) This simply applies a gain factor K to each input value:

3. PURE DELAY FILTER: y_n = x_n-1

The output value at time t = nh is simply the input at time t = (n-1)h, i.e. the signal is delayed by time h:

4. TWO-TERM DIFFERENCE FILTER: y_n = x_n - x_n-1

 The output value at t = nh is equal to the difference between the current input xn and the previous input x_n-1:

 5. TWO-TERM AVERAGE FILTER: y_n = (x_n + x_n-1) / 2

The output is the average (arithmetic mean) of the current and previous input:

6. THREE-TERM AVERAGE FILTER: yn = (xn + xn-1 + xn-2) / 3

This is similar to the previous example, with the average being taken of the current and two previous inputs.

7. CENTRAL DIFFERENCE FILTER: y_n = (x_n - x_n-2) / 2

This is similar in its effect to example (4). The output is equal to half the change in the input signal over the previous two sampling intervals:

 ORDER OF A DIGITAL FILTER

The order of a digital filter can be defined as the number of previous inputs (stored in the processor's memory) used to calculate the current output.

This is illustrated by the filters given as examples in the previous section.

Example (1): y_n = x_n

This is a zero order filter, since the current output yn depends only on the current input xn and not on any previous inputs.

Example (2): y_n = Kx_n

The order of this filter is again zero, since no previous outputs are required to give the current output value.

Example (3): y_n = x_n-1

This is a first order filter, as one previous input (xn-1) is required to calculate y n. (Note that this filter is classed as first-order because it uses one previous input, even though the current input is not used).

Example (4): y_n = x_n - x_n-1

This is again a first order filter, since one previous input value is required to give the current output.

Example (5): y_n = (x_n + x_n-1) / 2

The order of this filter is again equal to 1 since it uses just one previous input value.

Example (6): y_n = (x_n + x_n-1 + x_n-2) / 3

To compute the current output yn, two previous inputs (xn-1 and xn-2) are needed; this is therefore a second-order filter.

Example (7): y_n = (x_n - x_n-2) / 2

The filter order is again 2, since the processor must store two previous inputs in

order to compute the current output. This is unaffected by the absence of an explicit xn-1 term in the filter expression.

Q) For each of the following filters, state the order of the filter and identify the values of its coefficients:

(a) yn = 2xn - xn-1                  A) Order = 1: a0 = 2, a1 = -1

(b) yn = xn-2        + 2xn-2 + xn-3     B) Order = 2: a0   = 0, a1        = 0, a2 = 1

(c) yn = xn - 2xn-1                  C) Order = 3: a0   = 1, a1        = -2, a2 = 2, a3 = 1

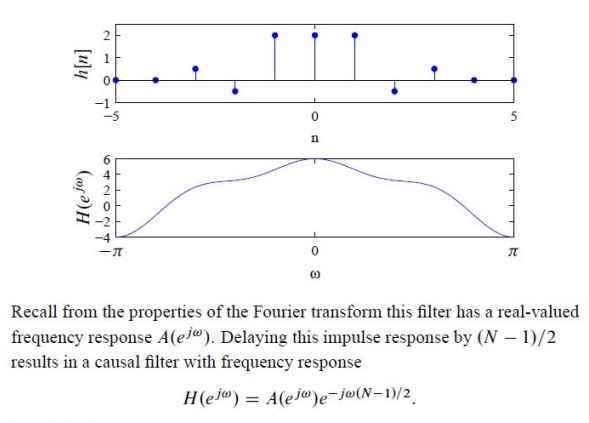
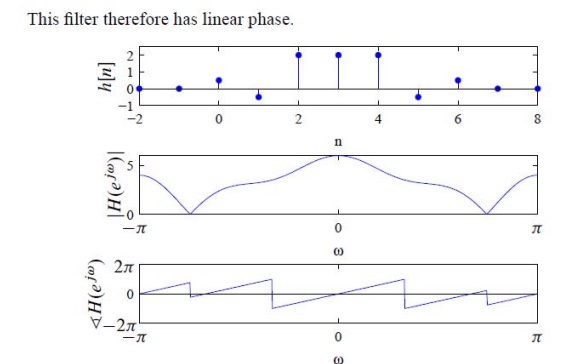
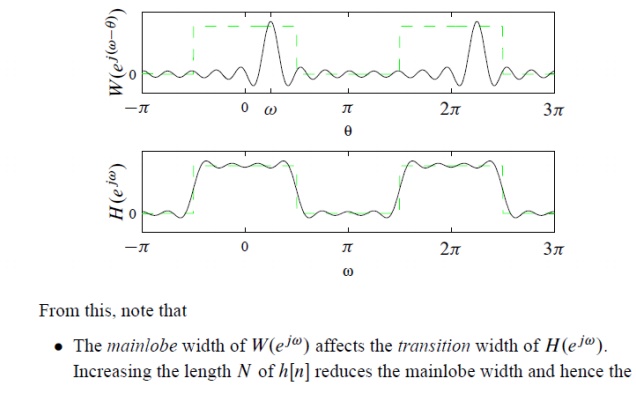
Number Representation

In digital signal processing, (B + 1)-bit fixed-point numbers are usually represented as two’s- complement signed fractions in the format

bo b-ib-2 …… b-B

The number represented is then

X = -bo + b-i2^{- 1} + b-22^{- 2} + ••• + b-B 2^-B (3.1)

where bo is the sign bit and the number range is —1 <X < 1. The advantage of this representation is that the product of two numbers in the range from — 1 to 1 is another number in the same range. Floating-point numbers are represented as

X = (-1)^s m2^c                         (3.2)

where s is the sign bit, m is the mantissa, and c is the characteristic or exponent. To make the representation of a number unique, the mantissa is normalized so that 0.5 <m < 1.

Although floating-point numbers are always represented in the form of (3.2), the way in which this representation is actually stored in a machine may differ. Since m > 0.5, it is not necessary to store the 2^{- 1} -weight bit of m, which is always set.

Therefore, in practice numbers are usually stored as    

X = (-1)^s(0.5 + f)2^c         (3.3)

where f is an unsigned fraction, 0 <f < 0.5.

Most floating- point processors now use the IEEE Standard 754 32-bit floating-point format for storing numbers. According to this standard the exponent is stored as an unsigned integer p where      

p = c + 126 (3.4)

Therefore, a number is stored as

X = ( -1)^s(0.5 + f )2^{p - 1 2 6} (3.5) where s is the sign bit, f is a 23-b unsigned fraction in the range 0 <f < 0.5, and p is an 8 -b unsigned integer in the range 0 <p < 255. The total number of bits is 1 + 23 + 8 = 32. For example, in IEEE format 3/4 is written (-1)⁰ (0.5 + 0.25)2° so s = 0, p = 126, and f = 0.25. The value X = 0 is a unique case and is represented by all bits zero (i.e., s = 0, f = 0, and p = 0). Although the 2^-1-weight mantissa bit is not actually stored, it does exist so the mantissa has 24 b plus a sign bit.

1. Fixed-Point Quantization Errors

In fixed- point arithmetic, a multiply doubles the number of significant bits. For example, the product of the two 5-b numbers 0.0011 and 0.1001 is the 10 -b number 00.000 110 11. The extra bit to the left of the decimal point can be discarded without introducing any error. However, the least significant four of the remaining bits must ultimately be discarded by some form of quantization so that the result can be stored to 5 b for use in other calculations. In the example above this results in 0.0010 (quantization by rounding) or 0.0001 (quantization by truncating). When a sum of products calculation is performed, the quantization can be performed either after each multiply or after all products have been summed with double-length precision.

We will examine three types of fixed-point quantization—rounding, truncation, and magnitude truncation. If X is an exact value, then the rounded value will be denoted Q_r (X), the truncated value Q_t (X), and the magnitude truncated value Q_{m t} (X). If the quantized value has B bits to the right of the decimal point, the quantization step size is

A = 2^-B                           (3.6)

Since rounding selects the quantized value nearest the unquantized value, it gives a value which is never more than ± A /2 away from the exact value. If we denote the rounding error by

fr = Qr(X) – X                 (3.7)

Truncation simply discards the low-order bits, giving a quantized value that is always less than or equal to the exact value so

- A < ft < 0 (3.9)

Magnitude truncation chooses the nearest quantized value that has a magnitude less than or equal to the exact value so

— A   <fmt <A     (3.10)

The error resulting from quantization can be modeled as a random variable uniformly distributed over the appropriate error range. Therefore, calculations with roundoff error can be considered error-free calculations that have been corrupted by additive white noise. 

2. Floating-Point Quantization Errors

With floating-point arithmetic it is necessary to quantize after both multiplications and additions. The addition quantization arises because, prior to addition, the mantissa of the smaller number in the sum is shifted right until the exponent of both numbers is the same. In general, this gives a sum mantissa that is too long and so must be quantized.

We will assume that quantization in floating-point arithmetic is performed by rounding. Because of the exponent in floating-point arithmetic, it is the relative error that is important.