Gibbs Phenomenon

GIBBS PHENOMENON

Consider the ideal LPF frequency response as shown in Fig 1 with a normalizing angular cut off frequency Ωc.

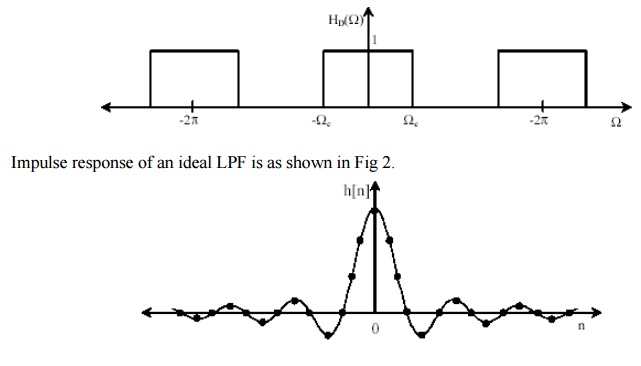
1. In Fourier series method, limits of summation index is -∞ to ∞. But filter must have finite terms. Hence limit of summation index change to -Q to Q where Q is some finite integer. But this type of truncation may result in poor convergence of the series. Abrupt truncation of infinite series is equivalent to multiplying infinite series with rectangular sequence. i.e at the point of discontinuity some oscillation may be observed in resultant series.

2. Consider the example of LPF having desired frequency response Hd (ω) as shown in figure. The oscillations or ringing takes place near band-edge of the filter.

3. This oscillation or ringing is generated because of side lobes in the frequency response W(ω) of the window function. This oscillatory behavior is called "Gibbs Phenomenon".

WINDO WING TECHNIQUE

W[n]

Windowing is the quickest method for designing an FIR filter. A windowing function simply truncates the ideal impulse response to obtain a causal FIR approximation that is non causal and infinitely long. Smoother window functions provide higher out-of band rejection in the filter response. However this smoothness comes at the cost of wider stopband transitions.

Various windowing method attempts to minimize the width of the main lobe (peak) of the frequency response. In addition, it attempts to minimize the side lobes (ripple) of the frequency response.

Rectangular Window: Rectangular This is the most basic of windowing methods. It does not require any operations because its values are either 1 or 0. It creates an abrupt discontinuity that results in sharp roll-offs but large ripples.

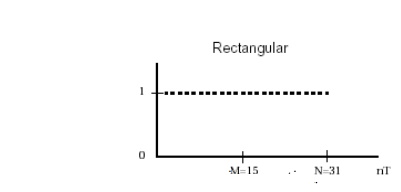
Rectangular window is defined by the following equation.

= 1 for 0 ≤ n ≤ N

= 0 otherwise

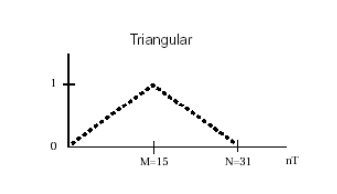
Triangular Window: The computational simplicity of this window, a simple convolution of two rectangle windows, and the lower sidelobes make it a viable alternative to the rectangular window.

Kaiser Window: This windowing method is designed to generate a sharp central peak. It has reduced side lobes and transition band is also narrow. Thus commonly used in FIR filter design.

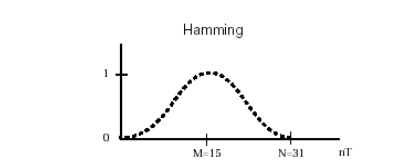
Hamming Window: This windowing method generates a moderately sharp central peak. Its ability to generate a maximally flat response makes it convenient for speech processing filtering.

Hanning Window: This windowing method generates a maximum flat filter design.