Chapter: Digital Signal Processing : FIR Filter Design
Important Short Questions and Answers: FIR Filter Design
FIR FILTER DESIGN
1.What is the condition satisfied by linear phase
FIR filter?
The
condition for constant phase delay are
Phase
delay, α = (N-1)/2 (i.e., phase delay is constant)
Impulse
response, h(n) = h(N-1-n) (i.e., impulse response is symmetric)
2.What are the desirable characteristics of the
frequency response of window function?
Advantages:
a)
FIR filters have exact linear phase.
b)
FIR filters are always stable.
c)
FIR filters can be realized in both recursive and
non recursive structure.
d)
Filters with any arbitrary magnitude response can
be tackled using FIR sequency.
Disadvantages:
a)
For the same filter specifications the order of FIR
filter design can be as high as 5 to n10 times that of IIR design.
b) Large
storage requirements needed.
c)
Powerful computational facilities required for the
implementation.
3.What
is meant by optimum equiripple design criterion.
The Optimum Equiripple design Criterion is used
for designing FIR Filters with Equal level filteration throughout the Design.
4.What
are the merits and demerits of FIR filters?
Merits:
1. FIR Filter is always stable.
2. FIR Filter with exactly linear phase can
easily be designed.
Demerits:
1. High Cost.
2.Require more Memory.
5.For
what type of filters frequency sampling method is suitable?
FIR FIlters
6.What
are the properties of FIR filters?
a)
FIR
Filter is always stable.
b)A Realizable filter can always be obtained.
7.What
is known as Gibbs phenomenon?
In the filter design by Fourier series method
the infinite duration impulse response is truncated to finite duration impulse
response at n= (N-1/2). The abrupt truncation of impulse introduces
oscillations in the pass band and stop band. This effect is known as Gibb’s
phenomenon.
8.Mention
various methods available for the design of FIR filter.Also list a few window
for the design of FIR filters.
There are three well known method of design
technique for linear phase FIR filter. They are
a)
Fourier
series method and window method
b) Frequency sampling method
c)
Optimal
filter design methods.
Windows: i.Rectangular ii.Hamming iii.Hanning
iv.Blackman v.Kaiser
9.List
any two advantages of FIR filters.
a)
FIR
filters have exact linear phase.
b)
FIR
filters are always stable.
c)
FIR
filters can be realized in both recursive and non recursive structure.
i.Direct form. ii.Cascade form
iii.Linear phase realization.
11.Mention
some design methods available to design FIR filter.
There are three well known method of
design technique for linear phase FIR filter. They are
a)
Fourier
series method and window method
b) Frequency sampling method
c)
Optimal
filter design methods.
Windows: i.Rectangular ii.Hamming
iii.Hanning iv.Blackman v.Kaiser
12.What
are FIR filters?
The specifications of the desired
filter will be given in terms of ideal frequency response Hd( ω). The impulse
response hd(n) of desired filter can
be obtained by inverse Fourier transform of hd(ω), which consists of infinite samples. The filters designed by selecting finite number of samples of
impulse response are called FIR filters.
13.What
are the conditions to be satisfied for constant phase delay in linear phase FIR
filter?
The condition for constant phase
delay are
Phase delay, α = (N-1)/2 (i.e.,
phase delay is constant) Impulse response, h(n) = h(N-1-n) (i.e., impulse
response is
symmetric)
14.What
is the reason that FIR filter is always stable?
FIR filter is always stable because
all its poles are at the origin.
There are four types of impulse
response for linear phase FIR filters
a)
Symmetric
impulse response when N is odd.
b) Symmetric impulse response when N is
even.
c)
Antisymmetric
impulse response when N is odd
d) Antisymmetric impulse response when
is even.
16.Write
the procedure for designing FIR filter using window.
1. Choose
the desired frequency response of the filter Hd (w)
2. Take
inverse Fourier transform of Hd(w) to obtain the desired impulse response hd
(n).
3.Choose
a window sequence w(n) and multiply hd(n) by w(n) to convert the infinite
duration impulse response to finite duration impulse response h(n).
4. The
Transfer function H(z) of the filter is obtained by taking z-transform of h(n).
17.Write the procedure for FIR filter design by
frequency sampling method.
1. Choose
the desired frequency response Hd(w).
2. Take
N-samples of Hd ( W) to generate the sequence H (K)
(Here H
bar of k should come)
3. Take
inverse of DFT of H (k) to get the impulse response h (n).
4. The
transfer function H (z) of the filter is obtained by taking z-transform of
impulse response.
a)
The width of the transition band depends on the
type of window.
b)
The width of the transition band can be made narrow
by increasing the value of N where N is the length of the window sequence.
c)
The attenuation in the stop band is fixed for a
given window, except in case of Kaiser Window where it is variable.
19.List the features of hanning window spectrum.
a)
The mainlobe width is equal to 8π/N.
b)
The maximum sidelobe magnitude is -31db.
c)
The sidelobe magnitude decreases with
increasing .
20. Compare the rectangular window and hanning
window.
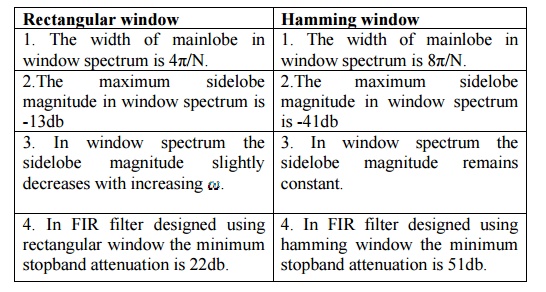
Rectangular window
1. The width of mainlobe in window spectrum is
4π/N.
2.The maximum sidelobe magnitude in window spectrum is
-13db
3. In window spectrum
the sidelobe magnitude slightly decreases with increasing.
4. In FIR filter designed using rectangular
window the minimum stopband attenuation is 22db.
1. The width of mainlobe in window spectrum is
8π/N.
2.The maximum sidelobe
magnitude in window spectrum is -41db
3. In window spectrum
the sidelobe magnitude remains constant.
4. In FIR filter designed using hamming window
the minimum stopband attenuation is 51db.
21.Compare Hamming window with Kaiser Window.
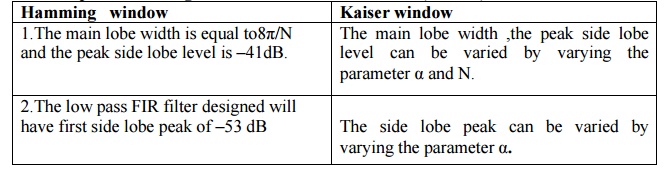
Hamming
window
1.The
main lobe width is equal to8π/N and the peak side lobe level is –41dB.
2.The low
pass FIR filter designed will have first side lobe peak of –53 dB
Kaiser window
1. The
main lobe width ,the peak side lobe level
can be varied
by varying the parameter α and N.
2. The
side lobe peak can be varied by varying the parameter α.
FIR Filters:
In the
Finite Impulse Response Filters the No.of. Impulses to be considered for
filtering are finite. There are no feed back Connections from the Output to the
Input. There are no Equivalent Structures of FIR filters in the Analog Regime.
Symmetric FIR Filters:
Symmetric
FIR Filters have their Impulses that occur as the mirror image in the first
quadrant and second quadrant or Third quadrant and fourth quadrant or both.
Anti Symmetric FIR Filters:
The
Antisymmetric FIR Filters have their impulses that occur as the mirror image in
the first quadrant and third quadrant or second quadrant and Fourth quadrant or
both.
Linear Phase:
The FIR
Filters are said to have linear in phase if the filter have the impulses that
increases according to the Time in digital domain.
Frequency Response:
The
Frequency response of the Filter is the relationship between the angular
frequency and the Gain of the Filter.
Gibbs Phenomenon:
The
abrupt truncation of Fourier series results in oscillation in both passband and
stop band. These oscillations are due to the slow convergence of the fourier
series. This is termed as Gibbs Phenomenon.
Windowing Technique:
To avoid
the oscillations instead of truncating the fourier co-efficients we are
multiplying the fourier series with a finite weighing sequence called a window
which has non-zero values at the required interval and zero values for other
Elements.
Quantization:
Total
number of bits in x is reduced by using two methods namely Truncation and
Rounding. These are known as quantization Processes.
Input Quantization Error:
The
Quantized signal are stored in a b bit register but for nearest values the same
digital equivalent may be represented. This is termed as Input Quantization
Error.
Product Quantization Error:
The
Multiplication of a b bit number with another b bit number results in a 2b bit
number but it should be stored in a b bit register. This is termed as Product
Quantization Error.
Co-efficient Quantization Error:
The
Analog to Digital mapping of signals due to the Analog Co-efficient
Quantization results in error due to the Fact that the stable poles marked at
the edge of the jΩ axis may be marked as an unstable pole in the digital
domain.
Limit Cycle Oscillations:
If the
input is made zero, the output should be made zero but there is an error occur
due to the quantization effect that the system oscillates at a certain band of
values.
Overflow limit Cycle oscillations:
Overflow
error occurs in addition due to the fact that the sum of two numbers may result
in overflow. To avoid overflow error saturation arithmetic is used.
Dead band:
The range
of frequencies between which the system oscillates is termed as Deadband of the
Filter. It may have a fixed positive value or it may oscillate between a
positive and negative value.
Signal scaling:
The
inputs of the summer is to be scaled first before execution of the addition
operation to find for any possibility of overflow to be occurred after
addition. The scaling factor s0 is multiplied with the inputs to avoid
overflow.
Related Topics