Overflow Oscillations

Overflow Oscillations:

With fixed-point arithmetic it is possible for filter calculations to overflow. This happens when two numbers of the same sign add to give a value having magnitude greater than one. Since numbers with magnitude greater than one are not representable, the result overflows. For example, the two’s complement numbers 0.101 (5/8) and 0.100 (4/8) add to give 1.001 which is the two’s complement representation of -7/8.

The overflow characteristic of two’s complement arithmetic can be represented as R{} where

An overflow oscillation, sometimesX+2 also X_referred<-1 to as an adder overflow limit cycle, is a high- level oscillation that can exist in an otherwise stable fixed-point filter due to the gross nonlinearity associated with the overflow of internal filter calculations [17]. Like limit cycles, overflow oscillations require recursion to exist and do not occur in nonrecursive FIR filters. Overflow oscillations also do not occur with floating-point arithmetic due to the virtual impossibility of overflow.

As an example of an overflow oscillation, once again consider the filter of (3.69) with 4-b fixed-point two’s complement arithmetic and with the two’s complement overflow characteristic of (3.71):

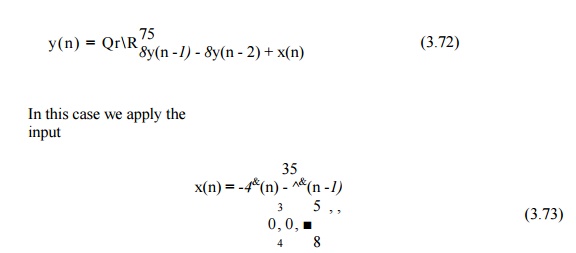
s to scale the filter calculations so as to render overflow impossible. However, this may unacceptably restrict the filter dynamic range. Another method is to force completed sums- of- products to saturate at ±1, rather than overflowing. It is important to saturate only the completed sum, since intermediate overflows in two’s complement arithmetic do not affect the accuracy of the final result. Most fixed-point digital signal processors provide for automatic saturation of completed sums if their saturation arithmetic feature is enabled. Yet another way to avoid overflow oscillations is to use a filter structure for which any internal filter transient is guaranteed to decay to zero [20]. Such structures are desirable anyway, since they tend to have low roundoff noise and be insensitive to coefficient quantization.

Coefficient Quantization Error:

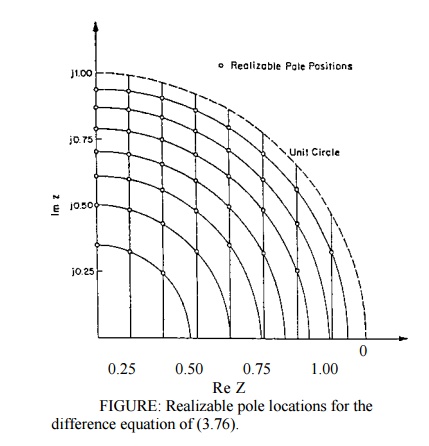
The sparseness of realizable pole locations near z = ± 1 will result in a large coefficient quantization error for poles in this region.

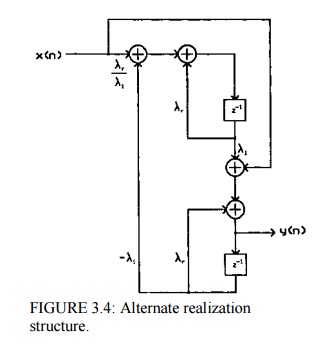
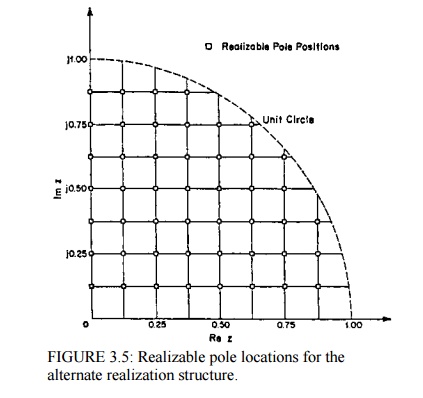
Figure3.4 gives an alternative structure to (3.77) for realizing the transfer function of (3.76). Notice that quantizing the coefficients of this structure corresponds to quantizing X_r and Xi. As shown in Fig.3.5 from, this results in a uniform grid of realizable pole locations. Therefore, large coefficient quantization errors are avoided for all pole locations.

It is well established that filter structures with low roundoff noise tend to be robust to coefficient quantization, and visa versa. For this reason, the uniform grid structure of Fig.3.4 is also popular because of its low roundoff noise. Likewise, the low-noise realizations can be expected to be relatively insensitive to coefficient quantization, and digital wave filters and lattice filters that are derived from low-sensitivity analog structures tend to have not only low coefficient sensitivity, but also low roundoff noise.

It is well known that in a high-order polynomial with clustered roots, the root location is a very sensitive function of the polynomial coefficients. Therefore, filter poles and zeros can be much more accurately controlled if higher order filters are realized by breaking them up into the parallel or cascade connection of first- and second-order subfilters. One exception to this rule is the case of linear- phase FIR filters in which the symmetry of the polynomial coefficients and the spacing of the filter zeros around the unit circle usually permits an acceptable direct realization using the convolution summation.

Given a filter structure it is necessary to assign the ideal pole and zero locations to the realizable locations. This is generally done by simplyrounding or truncatingthe filter coefficients to the available number of bits, or by assigning the ideal pole and zero locations to the nearest realizable locations. A more complicated alternative is to consider the original filter design problem as a problem in discrete

optimization, and choose the realizable pole and zero locations that give the best approximation to the desired filter response.