Register Allocation and Assignment

Register Allocation and Assignment

1 Global Register Allocation

2 Usage Counts

3 Register Assignment for Outer Loops

4 Register Allocation by Graph Coloring

5 Exercises for Section 8.8

Instructions involving only register operands are faster than those involving memory operands. On modern machines, processor speeds are often an order of magnitude or more faster than memory speeds. Therefore, efficient utilization of registers is vitally important in generating good code. This section presents various strategies for deciding at each point in a program what values should reside in registers (register allocation) and in which register each value should reside (register assignment).

One approach to register allocation and assignment is to assign specific values in the target program to certain registers. For example, we could decide to assign base addresses to one group of registers, arithmetic computations to another, the top of the stack to a fixed register, and so on.

This approach has the advantage that it simplifies the design of a code gener-ator. Its disadvantage is that, applied too strictly, it uses registers inefficiently; certain registers may go unused over substantial portions of code, while unnec-essary loads and stores are generated into the other registers. Nevertheless, it is reasonable in most computing environments to reserve a few registers for base

registers, stack pointers, and the like, and to allow the remaining registers to

be used by the code generator as it sees fit.

1. Global Register Allocation

The code generation algorithm in Section 8.6 used registers to hold values for the duration of a single basic block. However, all live variables were stored at the end of each block. To save some of these stores and corresponding loads, we might arrange to assign registers to frequently used variables and keep these registers consistent across block boundaries (globally). Since programs spend most of their time in inner loops, a natural approach to global register assignment is to try to keep a frequently used value in a fixed register throughout a loop. For the time being, assume that we know the loop structure of a flow graph, and that we know what values computed in a basic block are used outside that block. The next chapter covers techniques for computing this information.

One strategy for global register allocation is to assign some fixed number of registers to hold the most active values in each inner loop. The selected values may be different in different loops. Registers not already allocated may be used to hold values local to one block as in Section 8.6. This approach has the drawback that the fixed number of registers is not always the right number to make available for global register allocation. Yet the method is simple to implement and was used in Fortran H, the optimizing Fortran compiler developed by IBM for the 360-series machines in the late 1960s.

With early C compilers, a programmer could do some register allocation explicitly by using register declarations to keep certain values in registers for the duration of a procedure. Judicious use of register declarations did speed up many programs, but programmers were encouraged to first profile their programs to determine the program's hotspots before doing their own register allocation.

2. Usage Counts

In this section we shall assume that the savings to be realized by keeping a variable x in a register for the duration of a loop L is one unit of cost for each reference to x if x is already in a register. However, if we use the approach in Section 8.6 to generate code for a block, there is a good chance that after x has been computed in a block it will remain in a register if there are subsequent uses of x in that block. Thus we count a savings of one for each use of x in loop L that is not preceded by an assignment to x in the same block. We also save two units if we can avoid a store of x at the end of a block. Thus, if x is allocated a register, we count a savings of two for each block in loop L for which x is live on exit and in which x is assigned a value.

On the debit side, if x is live on entry to the loop header, we must load x into its register just before entering loop L. This load costs two units. Similarly, for each exit block B of loop L at which x is live on entry to some successor of B outside of L, we must store x at a cost of two. However, on the assumption that the loop is iterated many times, we may neglect these debits since they occur only once each time we enter the loop. Thus, an approximate formula for the benefit to be realized from allocating a register x within loop L is

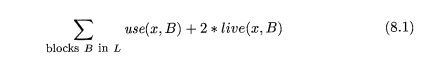
where use(x, B) is the number of times x is used in B prior to any definition of x;  live(x, B)  is 1 if x is live on exit from B and is assigned a value in B, and live(x, B) is 0 otherwise.  Note that (8.1) is approximate, because not all blocks in a loop are executed with equal frequency and also because  (8.1)  is based on the assumption that a loop is iterated many times. On specific machines a formula analogous to (8.1), but possibly quite different from it, would have to be developed.

Example 8 . 1 7 :  Consider the the basic blocks in the inner loop depicted in Fig. 8.17, where jump and conditional jump statements have been omitted. Assume registers RO, Rl, and R2 are allocated to hold values throughout the loop. Variables live on entry into and on exit from each block are shown in Fig. 8.17 for convenience, immediately above and below each block, respectively. There are some subtle points about live variables that we address in the next chapter. For example, notice that both e and f are live at the end of B1, but of these, only e is live on entry to B₂ and only f on entry to B₃. In general, the variables live at the end of a block are the union of those live at the beginning of each of its successor blocks.

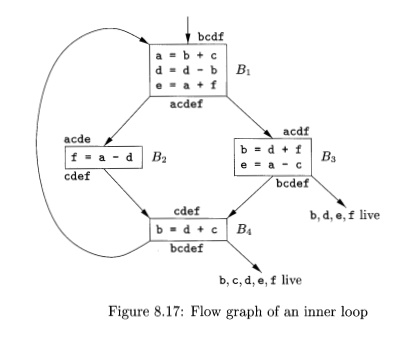
To evaluate (8.1) for x = a, we observe that a is live on exit from Bi and is assigned a value there, but is not live on exit from B₂, B₃, or B₄. Thus, J2B in L use(a._:B) — 2. Hence the value of (8.1) for x — a is 4. That is, four units of cost can be saved by selecting a for one of the global registers. The values of (8.1) for b, c, d, e, and f are 5, 3, 6, 4, and 4, respectively. 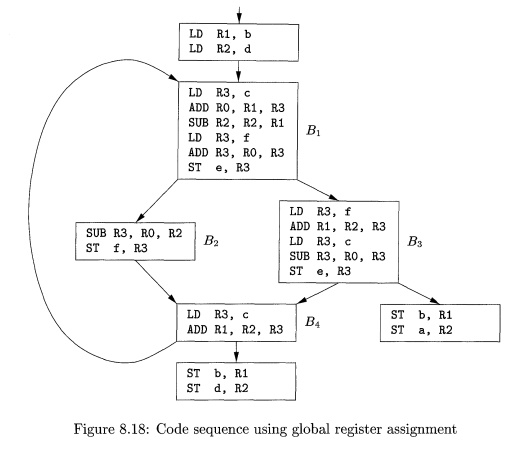Thus, we may select a, b, and d for registers RO, Rl, and R2, respectively. Using RO for e or f instead of a would be another choice with the same apparent benefit. Figure 8.18 shows the assembly code generated from Fig. 8.17, assuming that the strategy of Section 8.6 is used to generate code for each block. We do not show the generated code for the omitted conditional or unconditional jumps that end each block in Fig. 8.17, and we therefore do not show the generated code as a single stream as it would appear in practice.

3. Register Assignment for Outer Loops

Having assigned registers and generated code for inner loops, we may apply the same idea to progressively larger enclosing loops. If an outer loop L1 contains an inner loop L₂, the names allocated registers in L₂ need not be allocated registers in L1 — L2.  Similarly, if we choose to allocate x a register in L2    but not Li, we must load x on entrance to L2    and store x on exit from L2. We leave as an exercise the derivation of a criterion for selecting names to be allocated registers in an outer loop L, given that choices have already been made for all loops nested within L.

4. Register Allocation by Graph Coloring

When a register is needed for a computation but all available registers are in use, the contents of one of the used registers must be stored (spilled) into a memory location in order to free up a register. Graph coloring is a simple, systematic technique for allocating registers and managing register spills.

In the method, two passes are used. In the first,  target-machine instructions are selected as though there are an infinite number of symbolic registers; in effect, names used in the intermediate code become names of registers and the three-address instructions become machine-language instructions. If ac-cess to variables requires instructions that use stack pointers, display pointers, base registers, or other quantities that assist access, then we assume that these quantities are held in registers reserved for each purpose. Normally, their use is directly translatable into an access mode for an address mentioned in a machine instruction. If access is more complex, the access must be broken into several machine instructions, and a temporary symbolic register (or several) may need to be created.

Once the instructions have been selected, a second pass assigns physical registers to symbolic ones. The goal is to find an assignment that minimizes the cost of spills.

In the second pass, for each procedure a register-interference graph is con-structed in which the nodes are symbolic registers and an edge connects two nodes if one is live at a point where the other is defined. For example, a register-interference graph for Fig. 8.17 would have nodes for names a and d. In block By, a is live at the second statement, which defines d; therefore, in the graph there would be an edge between the nodes for a and d.

An attempt is made to color the register-interference graph using k colors, where k is the number of assignable registers. A graph is said to be colored if each node has been assigned a color in such a way that no two adjacent nodes have the same color. A color represents a register, and the color makes sure that no two symbolic registers that can interfere with each other are assigned the same physical register.

Although the problem of determining whether a graph is fc-colorable is NP - complete in general, the following heuristic technique can usually be used to do the coloring quickly in practice. Suppose a node n in a graph G has fewer than k neighbors (nodes connected to n by an edge). Remove n and its edges from G to obtain a graph G'. A ^-coloring of G' can be extended to a fc-coloring of G by assigning n a color not assigned to any of its neighbors.

By repeatedly eliminating nodes having fewer than k edges from the register-interference graph, either we obtain the empty graph, in which case we can produce a ^-coloring for the original graph by coloring the nodes in the reverse order in which they were removed, or we obtain a graph in which each node has k or more adjacent nodes. In the latter case a ^-coloring is no longer possible. At this point a node is spilled by introducing code to store and reload the register. Chaitin has devised several heuristics for choosing the node to spill. A general rule is to avoid introducing spill code into inner loops.

5. Exercises for Section 8.8

Exercise 8.8. 1 :    Construct the register-interference graph for the program in Fig. 8.17.                            

Exercise 8.8. 2:     Devise a register-allocation strategy on the  assumption that we automatically store all registers on the stack before each procedure call and restore them after the return.