Optimal Code Generation for Expressions

Optimal Code Generation for Expressions

1 Ershov Numbers

2 Generating Code From Labeled Expression Trees

3 Evaluating Expressions with an Insufficient Supply of Reg-isters

4 Exercises for Section 8.10

We can choose registers optimally when a basic block consists of a single expres-sion evaluation, or if we accept that it is sufficient to generate code for a block one expression at a time. In the following algorithm, we introduce a numbering scheme for the nodes of an expression tree (a syntax tree for an expression) that allows us to generate optimal code for an expression tree when there is a fixed number of registers with which to evaluate the expression.

1. Ershov Numbers

We begin by assigning to the nodes of an expression tree a number that tells how many registers are needed to evaluate that node without storing any tem-poraries. These numbers are sometimes called Ershov numbers, after A. Ershov, who used a similar scheme for machines with a single arithmetic register. For our machine model, the rules are:

1. Label any leaf 1.

2. The label of an interior node with one child is the label of its child.

3. The label of an interior node with two children is

(a)  The larger of the labels of its children, if those labels are different.

(b)  One plus the label of its children if the labels are the same.

E x a m p l e 8.23 : In Fig. 8.23 we see an expression tree (with operators omitted) that might be the tree for expression (a — b) + e x (c + d) or the three-address code:

t l  =  a  -  b

t 2  =  c  +  d

t 3  =  e  *  t 2

t 4  =  t l  +  t 3

Each of the five leaves is labeled 1 by rule (1). Then, we can label the interior node for tl = a - b , since both of its children are labeled. Rule (3b) applies, so it gets label one more than the labels of its children, that is, 2. The same holds for the interior node for t2 = c + d.

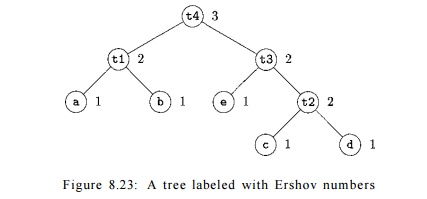
Now, we can work on the node for t3 = e * t 2 . Its children have labels 1 and 2, so the label of the node for t3 is the maximum, 2, by rule (3a). Finally, the root,  the  node  for t4 = tl + t 3 , has two children with label 2, and therefore it gets  label  3.

2. Generating Code From Labeled Expression Trees

It can be proved that, in our machine model, where all operands must be in registers, and registers can be used by both an operand and the result of an operation, the label of a node is the fewest registers with which the expression can be evaluated using no stores of temporary results. Since in this model, we are forced to load each operand, and we are forced to compute the result cor-responding to each interior node, the only thing that can make the generated code inferior to the optimal code is if there are unnecessary stores of tempo-raries. The argument for this claim is embedded in the following algorithm for generating code with no stores of temporaries, using a number of registers equal to the label of the root.

Algorithm 8 . 2 4 : Generating code from a labeled expression tree.

INPUT : A labeled tree with each operand appearing once (that is, no common subexpressions).

OUTPUT : An optimal sequence of machine instructions to evaluate the root

into a register.

METHOD : The following is a recursive algorithm to generate the machine code. The steps below are applied, starting at the root of the tree. If the algorithm is applied to a node with label k, then only k registers will be used. However, there is a "base" 6 > 1 for the registers used so that the actual registers used are Rb,Rb+i,- --Rb+k-i- The result always appears in R_b+k-i-

   To generate machine code for an interior node with label k and two chil-dren with equal labels (which must be k — 1) do the following:

            Recursively generate code for the right child, using base 6 + 1. The result of the right child appears in register Rb+k •

            Recursively generate code for the left child, using base 6; the result appears in Rb+k-i-

           Generate the instruction OP Rb+k,Rb+k-i,Rb+k, where OP is the appropriate operation for the interior node in question.

Suppose we have an interior node with label k and children with unequal

labels.  Then one of the children, which we'll call the  "big"  child, has label k, and the other child, the  "little"  child, has some  label  m <  k.  Do the following to generate code for this  interior node, using base 6: 

Recursively generate code for the big child, using base b; the result appears in register Rb+k-i-

Recursively generate code for the small child, using base 6; the result appears  in register Rb+m-1.  Note that  since m  <  k,  neither  Rb+k-i nor any  higher-numbered register is used.     

(c)  Generate the instruction  OP Rb+k-i, Rb+m-i, Rb+k-i  or  the  instruction  OP Rb+k-i, Rb+k-i, Rb+m-i5    depending on whether  the big child is the right or left child, respectively.      

For a leaf representing operand x, if the base is 6 generate the instruction LD Rb, x.

Example  8 . 2 5 :  Let  us  apply  Algorithm  8.24 to the tree of  Fig.  8.23.  Since the label  of the  root  is  3, the  result will  appear in R3,  and  only  Ry,  R2,  and R3 will be used. The base for the root is b = 1. Since the root has children of equal labels, we generate code for the right child first, with base 2.

When we generate code for the right child of the root, labeled t3, we find the big child is the right child and the little child is the left child. We thus generate code for the right child first, with 6 = 2. Applying the rules for equal-labeled children and leaves, we generate the following code for the node labeled ii:

LD  R3,  D

LD  R2,  C

ADD R3,  R2,  R3

Next, we generate code for the left child of the right child of the root; this node is the leaf labeled e. Since b — 2, the proper instruction is

LD R2, e

Now we can complete the code for the right child of the root by adding the instruction

MUL R3,  R2, R3

The algorithm proceeds to generate code for the left child of the root, leaving the result in R₂, and with base 1. The complete sequence of instructions is shown in Fig. 8.24.

LD  R3,  d 

LD  R2,  c 

ADD R3,  R2, R3

LD  R2,  e 

MUL R3,  R2,  R3

LD  R2,  b 

LD  Rl,  a 

SUB R2,  Rl,  R2

ADD R3,  R2, R3

Figure 8.24: Optimal three-register code for the tree of Fig. 8.23

3. Evaluating Expressions with an Insufficient Supply of Registers

When there are fewer registers available than the label of the root of the tree, we cannot apply Algorithm 8.24 directly. We need to introduce some store instructions that spill values of subtrees into memory, and we then need to load those values back into registers as needed. Here is the modified algorithm that takes into account a limitation on the number of registers.

Algorithm 8 . 2 6 :  Generating code from a labeled expression tree.

INPUT : A labeled tree with each operand appearing once (i.e., no common subexpressions) and a number of registers r > 2.

OUTPUT : An optimal sequence of machine instructions to evaluate the root into a register, using no more than r registers, which we assume are Ri, R₂, •.. ,R_r-

METHOD : Apply the following recursive algorithm, starting at the root of the tree, with base 6 = 1. For a node JV with label r or less, the algorithm is exactly the same as Algorithm 8.24, and we shall not repeat those steps here. However, for interior nodes with a label k > r, we need to work on each side of the tree separately and store the result of the larger subtree. That result is brought back into memory just before node iV is evaluated, and the final step will take place in registers R_r-1 and R_r- The modifications to the basic algorithm are as follows:

1. Node N has at least one child with label r or greater. Pick the larger child (or either if their labels are the same) to be the "big" child and let the other child be the "little" child.

2. Recursively generate code for the big child, using base 6 = 1. The result of this evaluation will appear in register Rr.    

3. Generate the machine instruction ST tk,Rr, Where is a temporary variable used for temporary results used to help  evaluate nodes with label k.           

4. Generate code for the little child as follows.  If the little child has label r or greater, pick base 6 = 1 . If the label of the little child is j < r, then pick 6 = r — j.  Then recursively apply this algorithm to the little child; the  result appears in  Rr.        

5. Generate the  instruction  LD  Rr^i,tk-      

6. If the big child is  the  right child  of N, then  generate the instruction OP Rr, Rr, Rr-1. If the big child is the left child, generate OP Rr, Rr-i, Rr-

E x a m p l e 8 . 2 7 : Let us revisit the expression represented by Fig. 8.23, but now assume that r = 2; that is, only registers Rl and R2 are available to hold tem-poraries used in the evaluation of expressions. When we apply Algorithm 8.26 to Fig. 8.23, we see that the root, with label 3, has a label that is larger than r = 2. Thus, we need to identify one of the children as the "big" child. Since they have equal labels, either would do. Suppose we pick the right child as the big child.

Since the label of the big child of the root is 2, there are enough registers. We thus apply Algorithm 8.24 to this subtree, with 6 = 1 and two registers. The result looks very much like the code we generated in Fig. 8.24, but with registers Rl and R2 in place of R2 and R3. This code is

LD    R2,    d      

LD    Rl,     c       

ADD R2,   Rl,     R2

LD    Rl,     e       

MUL R2,   Rl,     R2

Now, since we need both registers for the left child of the root, we need to generate the instruction

ST t3,  R2

Next, the left child of the root is handled. Again, the number of registers is sufficient for this child, and the code is

LD R2,  b

LD Rl,  a

SUB R2,  Rl,  R2

Finally, we reload the temporary that holds the right child of the root with the instruction

LD Rl,  t3

and execute the operation at the root of the tree with the instruction

ADD R2,  R2, Rl

The complete sequence of instructions is shown in Fig. 8.25.

LD    R2     d      

LD    Rl      c       

ADD R2     Rl,     R2

LD    Rl      e       

MUL R2     Rl,     R2

ST     t3      R2    

LD    R2     b      

LD    Rl      a       

SUB R2     Rl,     R2

LD    Rl      t3     

ADD R2     R2, Rl

Figure 8.25: Optimal three-register code for the tree of Fig. 8.23, using only two registers

4. Exercises for Section 8.10

Exercise 8 . 1 0 . 1 :  Compute Ershov numbers for the following expressions:

a)  a/(b + c) - d* (e + / ) .

b)  a + b * (c * (d + e)).

 (—a   +   *p)*((b-*q)/(—c+*r)).

Exercise 8 . 1 0 . 2:  Generate optimal code using two registers for each of the

expressions of Exercise 8.10.1.

Exercise 8 . 1 0 . 3:  Generate optimal code using three registers for each of the

expressions of Exercise 8.10.1.

! Exercise 8. 1 0.4: Generalize the computation of Ershov numbers to expression trees with interior nodes with three or more children.

! Exercise 8.10.5: An assignment to an array element, such as a [ i ] = x, ap-pears to be an operator with three operands: a, i, and x. How would you modify the tree-labeling scheme to generate optimal code for this machine model?

  Exercise 8 . 1 0 . 6 : The original Ershov numbers were used for a machine that allowed the right operand of an expression to be in memory, rather than a register. How would you modify the tree-labeling scheme to generate optimal code for this machine model?

  Exercise 8 . 1 0 . 7: Some machines require two registers for certain single-pre-cision values. Suppose that the result of a multiplication of single-register quan-tities requires two consecutive registers, and when we divide a/6, the value of a must be held in two consecutive registers. How would you modify the tree-labeling scheme to generate optimal code for this machine model?