Optimization of Basic Blocks

Optimization of Basic Blocks

1 The DAG Representation of Basic Blocks

2 Finding Local Common Subexpressions

3 Dead Code Elimination

4 The Use of Algebraic Identities

5 Representation of Array References

6 Pointer Assignments and Procedure Calls

7 Reassembling Basic Blocks From DAG's

8 Exercises for Section 8.5

We can often obtain a substantial improvement in the running time of code merely by performing local optimization within each basic block by itself. More thorough global optimization, which looks at how information flows among the basic blocks of a program, is covered in later chapters, starting with Chapter 9. It is a complex subject, with many different techniques to consider.

1. The DAG Representation of Basic Blocks

Many important techniques for local optimization begin by transforming a basic block into a DAG (directed acyclic graph). In Section 6.1.1, we introduced the DAG as a representation for single expressions. The idea extends naturally to the collection of expressions that are created within one basic block. We construct a DAG for a basic blockas follows:

1. There is a node in the DAG for each of the initial values of the variables appearing in the basic block.

2. There is  a node N  associated with each  statement  s  within  the block. The children of N are those nodes corresponding to statements that are the last definitions, prior to s, of the operands used by s.

3. Node N is labeled by the operator applied at s, and also attached to N is the list of variables for which it is the last definition within the block.

4. Certain nodes  are designated  output nodes. These are the nodes whose variables  are  live  on  exit from the block; that  is,  their values  may be used later, in another block of the flow graph. Calculation of these "live variables" is a matter for global flow analysis, discussed in Section 9.2.5.

The DAG representation of a basic block lets us perform several code-improving transformations on the code represented by the block.

    We can eliminate local common subexpressions, that is, instructions that compute a value that has already been computed.

    We can eliminate dead code, that is, instructions that compute a value that is never used.

    We can reorder statements that do not depend on one another; such reordering may reduce the time a temporary value needs to be preserved in a register.

We can apply algebraic laws to reorder operands of three-address instruc-tions, and sometimes thereby simplify the computation.

2. Finding Local Common Subexpressions

Common subexpressions can be detected by noticing, as a new node M is about to be added, whether there is an existing node N with the same children, in the same order, and with the same operator. If so, TV computes the same value as M and may be used in its place. This technique was introduced as the "value-number" method of detecting common subexpressions in Section 6.1.1.

Example 8 . 1 0 :  A DAG for the block

a = b + c

b = a - d c = b + c

d = a – d

is shown in Fig.  8.12. When we construct the node for the third statement c = b + c, we know that the use of b in b + c refers to the node of Fig. 8.12 labeled -,  because that is the most recent definition of b. Thus, we do not confuse the values computed at statements one and three.

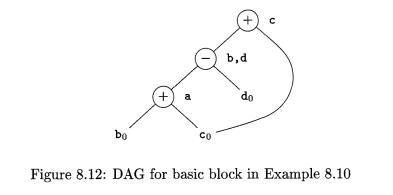
However, the node corresponding to the fourth statement d = a - d has the operator - and the nodes with attached variables a and do as children. Since the operator and the children are the same as those for the node corresponding to statement two, we do not create this node, but add d to the list of definitions for the node labeled —. •

It might appear that, since there are only three nonleaf nodes in the DAG of Fig. 8.12, the basic block in Example 8.10 can be replaced by a block with only three statements. In fact, if b is not live on exit from the block, then we do not need to compute that variable, and can use d to receive the value represented by the node labeled —. in Fig. 8.12. The block then becomes

However, if both b and d are live on exit, then a fourth statement must be used to copy the value from one to the other.¹

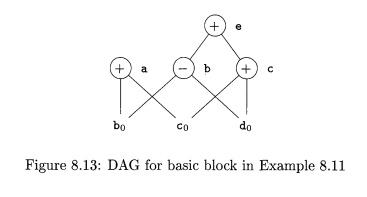
E x a m p l e 8.11: When we look for common subexpressions, we really are look-ing for expressions that are guaranteed to compute the same value, no matter how that value is computed. Thus, the DAG method will miss the fact that the expression computed by the first and fourth statements in the sequence

a        =       b        +       c;

b        =       b        -        d

c        =       c        +       d

e  = b  +  c

is the same, namely bo 4- en. That is, even though b and c both change between the first and last statements, their sum remains the same, because b + c = (b - d) + (c + d). The DAG for this sequence is shown in Fig. 8.13, but does not exhibit any common subexpressions. However, algebraic identities applied to the DAG, as discussed in Section 8.5.4, may expose the equivalence.

3. Dead Code Elimination

The operation on DAG's that corresponds to dead-code elimination can be im-plemented as follows. We delete from a DAG any root (node with no ancestors) that has no live variables attached. Repeated application of this transformation will remove all nodes from the DAG that correspond to dead code.

Example 8.12: If, in Fig. 8.13, a and b are live but c and e are not, we can immediately remove the root labeled e. Then, the node labeled c becomes a root and can be removed. The roots labeled a and b remain, since they each have live variables attached. •

4. The Use of Algebraic Identities

Algebraic identities represent another important class of optimizations on basic blocks. For example, we may apply arithmetic identities, such as

to eliminate computations from a basic block.

Another class of algebraic optimizations includes local reduction in strength, that is, replacing a more expensive operator by a cheaper one as in:

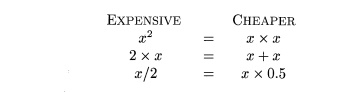
A third class of related optimizations is constant folding. Here we evaluate constant expressions at compile time and replace the constant expressions by their values.² Thus the expression 2 * 3 . 1 4 would be replaced by 6 . 2 8 . Many constant expressions arise in practice because of the frequent use of symbolic constants in programs.

The DAG-construction process can help us apply these and other more general algebraic transformations such as commutativity and associativity. For example, suppose the language reference manual specifies that * is commutative; that is, x*y = y*x. Before we create a new node labeled * with left child M and right child N, we always check whether such a node already exists. However, because * is commutative, we should then check for a node having operator *, left child N, and right child M.

The relational operators such as < and — sometimes generate unexpected common subexpressions. For example, the condition x > y can also be tested by subtracting the arguments and performing a test on the condition code set by the subtraction.³ Thus, only one node of the DAG may need to be generated for x — y and x > y.

Associative laws might also be applicable to expose common subexpressions. For example, if the source code has the assignments

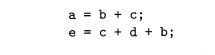
the following intermediate code might be generated:

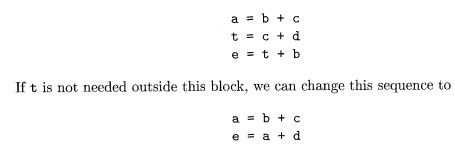
using both the associativity and commutativity of +.

The compiler writer should examine the language reference manual care-fully to determine what rearrangements of computations are permitted, since (because of possible overflows or underflows) computer arithmetic does not al-ways obey the algebraic identities of mathematics. For example, the Fortran standard states that a compiler may evaluate any mathematically equivalent expression,  provided that the integrity of parentheses is not violated.  Thus, a compiler may evaluate x * y — x * z a,s x * (y - z), but it may not evaluate a + (6 — c) as (a + b) — c. A Fortran compiler must therefore keep track of where parentheses were present in the source language expressions if it is to optimize programs in accordance with the language definition.

5. Representation of Array References

At first glance, it might appear that the array-indexing instructions can be treated like any other operator. Consider for instance the sequence of three-address statements:

If we think of a [ i ]  as an operation involving a and  i, similar to a + i, then it might appear as if the two uses of a [ i ] were a common subexpression. In that case, we might be tempted to "optimize" by replacing the third instruction z  =  a [ i ]  by the simpler z  =  x. However, since j  could equal i, the middle statement may in fact change the value of a [ i ] ; thus, it is not legal to make this change.         

The proper way to represent array accesses in a DAG is as follows. 

1. An assignment from an array, like x  = a [ i ] , is represented by creating a node with operator =[] and two children representing the initial value of the array, a0   in this case, and the index i.  Variable x becomes a label of this new node.         

2. An assignment to an array, like a [ j ] =  y, is represented by a new node with operator []= and three children representing a 0 , j and y. There is no variable labeling this node. What is different is that the creation of   this node kills all currently constructed nodes whose value depends on a ₀ . A node that has been killed cannot receive any more labels; that is, it cannot become a common subexpression.

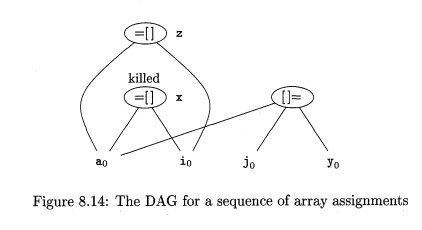
Example 8 . 1 3 :  The DAG for the basic block

x = a [ i ]

a [ j ] =  y

z = a [ i ]

is shown in Fig- 8.14. The node N for x is created first, but when the node labeled [ ] = is created, N is killed.  Thus, when the node for z is created, it cannot be identified with N, and a new node with the same operands a0    and i0    must be created instead.

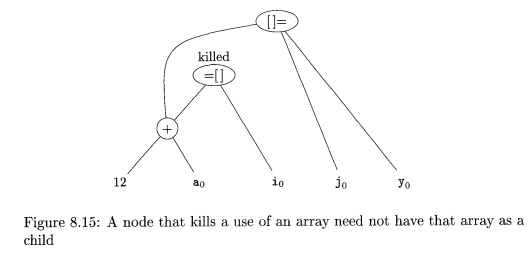
Example 8 . 14: Sometimes, a node must be killed even though none of its children have an array like a0 in Example 8.13 as attached variable. Likewise, a node can kill if it has a descendant that is an array, even though none of its children are array nodes. For instance, consider the three-address code

b = 12 + a

x = b [ i ]

b [ j ] = y

What is happening here is that, for efficiency reasons, b has been defined to be a position in an array a. For example, if the elements of a are four bytes long, then b represents the fourth element of a. If j and i represent the same value, then b [ i ] and b [ j ] represent the same location. Therefore it is important to have the third instruction, b [ j ] = y, kill the node with x as its attached variable. However, as we see in Fig. 8.15, both the killed node and the node that does the killing have cio as a grandchild, not as a child.

6. Pointer Assignments and Procedure Calls

When we assign indirectly through a pointer, as in the assignments

x = *p

*q = y

we do not know what p or q point to. In effect, x = *p is a use of every variable whatsoever, and *q = y is a possible assignment to every variable. As a consequence, the operator =* must take all nodes that are currently associated with identifiers as arguments, which is relevant for dead-code elimination. More importantly, the *= operator kills all other nodes so far constructed in the DAG.

There are global pointer analyses one could perform that might limit the set of variables a pointer could reference at a given place in the code. Even local analysis could restrict the scope of a pointer. For instance, in the sequence

p = &x 

*p = y

we know that x, and no other variable, is given the value of y, so we don't need to kill any node but the node to which x was attached.

Procedure calls behave much like assignments through pointers. In the absence of global data-flow information, we must assume that a procedure uses and changes any data to which it has access. Thus, if variable x is in the scope of a procedure P, a call to P both uses the node with attached variable x and kills that node.

7. Reassembling Basic Blocks From DAG's

After we perform whatever optimizations are possible while constructing the DAG or by manipulating the DAG once constructed, we may reconstitute the three-address code for the basic block from which we built the DAG. For each  node that has one or more attached variables, we construct a three-address statement that computes the value of one of those variables. We prefer to compute the result into a variable that is live on exit from the block. However, if we do not have global live-variable information to work from, we need to assume that every variable of the program (but not temporaries that are generated by the compiler to process expressions) is live on exit from the block.

If the node has more than one live variable attached, then we have to in-troduce copy statements to give the correct value to each of those variables. Sometimes, global optimization can eliminate those copies, if we can arrange to use one of two variables in place of the other.

Example 8 . 1 5 : Recall the DAG of Fig. 8.12. In the discussion following Example 8.10, we decided that if b is not live on exit from the block, then the three statements

a = b + c

d = a - d

c = d + c

suffice to reconstruct the basic block. The third instruction, c = d + c, must use d as an operand rather than b, because the optimized block never computes b.

If both b and d are live on exit, or if we are not sure whether or not they are live on exit, then we need to compute b as well as d. We can do so with the sequence

a = b + c

d = a - d

b = d 

c = d + c

This basic block is still more efficient than the original. Although the number of instructions is the same, we have replaced a subtraction by a copy, which tends to be less expensive on most machines. Further, it may be that by doing a global analysis, we can eliminate the use of this computation of b outside the block by replacing it by uses of d. In that case, we can come back to this basic block and eliminate b = d later. Intuitively, we can eliminate this copy if wherever this value of b is used, d is still holding the same value. That situation may or may not be true, depending on how the program recomputes d. •

When reconstructing the basic block from a DAG, we not only need to worry about what variables are used to hold the values of the DAG's nodes, but we also need to worry about the order in which we list the instructions computing the values of the various nodes. The rules to remember are

1. The order of instructions must respect the order of nodes in the DAG. That is, we cannot compute a node's value until we have computed a value for each of its children.

2. Assignments to an array must follow all previous assignments to, or eval-uations from, the same array, according to the order of these instructions in the original basic block.

    Evaluations of array elements must follow any previous (according to the original block) assignments to the same array. The only permutation allowed is that two evaluations from the same array may be done in either order, as long as neither crosses over an assignment to that array.

    Any use of a variable must follow all previous (according to the original block) procedure calls or indirect assignments through a pointer.

    Any procedure call or indirect assignment through a pointer must follow all previous (according to the original block) evaluations of any variable.

That is, when reordering code, no statement may cross a procedure call or assignment through a pointer, and uses of the same array may cross each other only if both are array accesses, but not assignments to elements of the array.

8. Exercises for Section 8.5

Exercise 8 . 5 . 1 :  Construct the DAG for the basic block

d = b * c

e = a + b

b = b * c

a =  e  -  d

Exercise 8 . 5 . 2:  Simplify the three-address code of Exercise 8.5.1, assuming

 Only a is live on exit from the block.

 a, b, and c are live on exit from the block.

Exercise 8 . 5 . 3 : Construct the basic block for the code in block B6 of Fig. 8.9.

Do not forget to include the comparison i < 10.

Exercise 8 . 5 . 4 : Construct the basic block for the code in block B3 of Fig. 8.9.

Exercise 8 . 5 . 5 : Extend Algorithm 8.7 to process three-statements of the form

a)  a [ i ] =  b

b)  a  =  b [ i ]

 a  =  *b

 *a  =  b

Exercise 8 . 5 . 6 :  Construct the DAG for the basic block

a [ i ] = b

*p = c 

 =  a [ j ]

 =  *p

*p  =  a [ i ]

on the assumption that

    p can point anywhere.

    p can point only to b or d.

Exercise 8 . 5 . 7 : If a pointer or array expression, such as a [ i ] or *p is assigned and then used, without the possibility of being changed in the interim, we can take advantage of the situation to simplify the DAG. For example, in the code of Exercise 8.5.6, since p is not assigned between the second and fourth statements, the statement e = *p can be replaced by e = c, regardless of what p points to. Revise the DAG-construction algorithm to take advantage of such situations,         and apply your algorithm to the code of Example 8.5.6.

Exercise 8 . 5 . 8 :  Suppose a basic block is formed from the C assignment statements

         x        =       a +     b        +  c  +  d +  e  +  f;

         y        =       a +     c        +  e;

     Give the three-address statements (only one addition per statement) for this block.

     Use the associative and commutative laws to modify the block to use the fewest possible number of instructions, assuming both x and y are live on exit from the block.