Instruction Selection by Tree Rewriting

Instruction Selection by Tree Rewriting

1 Tree-Translation Schemes

2 Code Generation by Tiling an Input Tree

3 Pattern Matching by Parsing

4 Routines for Semantic Checking

5 General Tree Matching

6 Exercises for Section 8.9

Instruction selection can be a large combinatorial task, especially on machines that are rich in addressing modes, such as CISC machines, or on machines with special-purpose instructions, say, for signal processing. Even if we assume that the order of evaluation is given and that registers are allocated by a separate mechanism, instruction selection — the problem of selecting target-language instructions to implement the operators in the intermediate representation — remains a large combinatorial task.

In this section, we treat instruction selection as a tree-rewriting problem. Tree representations of target instructions have been used effectively in code-generator generators, which automatically construct the instruction-selection phase of a code generator from a high-level specification of the target machine. Better code might be obtained for some machines by using DAG's rather than trees, but DAG matching is more complex than tree matching.

1. Tree-Translation Schemes

Throughout this section, the input to the code-generation process will be a sequence of trees at the semantic level of the target machine. The trees are what we might get after inserting run-time addresses into the intermediate representation, as described in Section 8.3. In addition, the leaves of the trees contain information about the storage types of their labels.

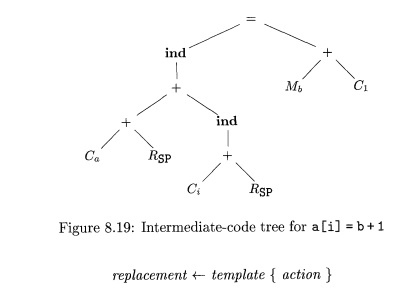
Example 8 . 1 8 : Figure  8.19  contains  a tree  for  the  assignment statement a [ i ] = b + l , where the array a is stored on the run-time stack and the variable b is a global in memory location The run-time addresses of locals a and i are given as constant offsets Ca    and Ci from SP, the register containing the pointer to the beginning of the current activation record. 

The assignment to a [ i ]  is an indirect assignment in which the  r-value of the location for a [ i ] is set to the r-value of the expression b+ 1.  The addresses of array a and variable i are given by adding the values of the constant Ca    and Ci, respectively, to the contents of register SP. We simplify array-address calcu-lations by assuming that all values are one-byte characters. (Some instruction sets make special provisions for multiplications by constants, such as 2, 4, and 8, during address calculations.)

In the tree, the ind operator treats its argument as a memory address. As the left child of an assignment operator, the ind node gives the location into which the r-value on the right side of the assignment operator is to be stored. If an argument of a + or ind operator is a memory location or a register, then the contents of that memory location or register are taken as the value. The leaves in the tree are labeled with attributes; a subscript indicates the value of the attribute. •

The target code is generated by applying a sequence of tree-rewriting rules to reduce the input tree to a single node. Each tree-rewriting rule has the form

where replacement is a single node, template is a tree, and action is a code fragment, as in a syntax-directed translation scheme.

A set of tree-rewriting rules is called a tree-translation scheme.

Each tree-rewriting rule represents the translation of a portion of the tree given by the template. The translation consists of a possibly empty sequence of machine instructions that is emitted by the action associated with the template. The leaves of the template are attributes with subscripts, as in the input tree. Sometimes, certain restrictions apply to the values of the subscripts in the templates; these restrictions are specified as semantic predicates that must be satisfied before the template is said to match. For example, a predicate might specify that the value of a constant fall in a certain range.

A tree-translation scheme is a convenient way to represent the instruction-selection phase of a code generator. As an example of a tree-rewriting rule, consider the rule for the register-to-register add instruction:

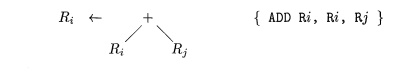
This rule is used as follows. If the input tree contains a subtree that matches this tree template, that is, a subtree whose root is labeled by the operator + and whose left and right children are quantities in registers i and j, then we can replace that subtree by a single node labeled Ri and emit the instruction ADD Ri,Ri,Rj as output. We call this replacement a tiling of the subtree. More than one template may match a subtree at a given time; we shall describe shortly some mechanisms for deciding which rule to apply in cases of conflict.

E x a m p l e 8 . 1 9 : Figure 8.20 contains tree-rewriting rules for a few instructions of our target machine. These rules will be used in a running example throughout this section. The first two rules correspond to load instructions, the next two to store instructions, and the remainder to indexed loads and additions. Note that rule (8) requires the value of the constant to be 1. This condition would be specified by a semantic predicate. •

2. Code Generation by Tiling an Input Tree

A tree-translation scheme works as follows. Given an input tree, the templates in the tree-rewriting rules are applied to tile its subtrees. If a template matches, the matching subtree in the input tree is replaced with the replacement node of the rule and the action associated with the rule is done. If the action contains a sequence of machine instructions, the instructions are emitted. This process is repeated until the tree is reduced to a single node, or until no more templates match. The sequence of machine instructions generated as the input tree is reduced to a single node constitutes the output of the tree-translation scheme on the given input tree.

The process of specifying a code generator becomes similar to that of us-ing a syntax-directed translation scheme to specify a translator. We write a tree-translation scheme to describe the instruction set of a target rnachine. In practice, we would like to find a scheme that causes a minimal-cost instruction sequence to be generated for each input tree. Several tools are available to help build a code generator automatically from a tree-translation scheme.

Example 8 . 2 0 : Let us use the tree-translation scheme in Fig. 8.20 to generate code for the input tree in Fig. 8.19. Suppose that the first rule is applied to load the constant C_a into register RO:

The label of the leftmost leaf then changes from Ca    to R0    and the instruction LD RO, #a is generated. The seventh rule now matches the leftmost subtree with root labeled +:

Using this rule, we rewrite this subtree as a single node labeled RQ and generate the instruction ADD RO, RO, SP. Now the tree looks like

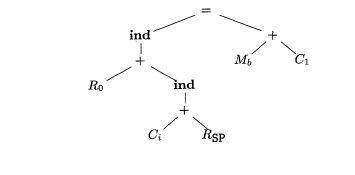
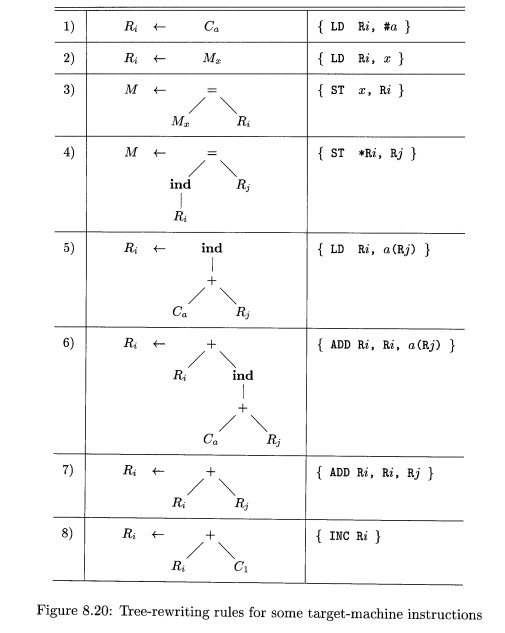
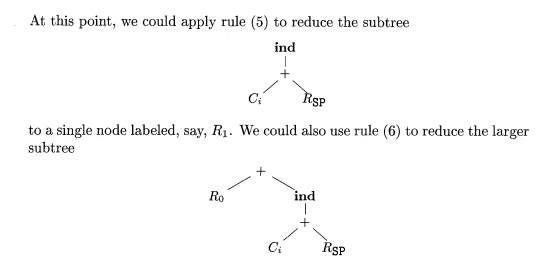
to a single node labeled Ro and generate the instruction ADD RO, RO, i(SP). Assuming that it is more efficient to use a single instruction to compute the larger subtree rather than the smaller one, we choose rule (6) to get

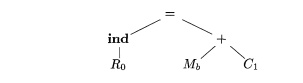
In the right subtree, rule (2) applies to the leaf It generates an instruction to load b into register Rl, say. Now, using rule (8) we can match the subtree

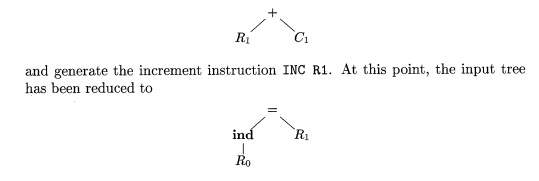
This remaining tree is matched by rule (4), which reduces the tree to a single node and generates the instruction ST *R0, Rl. We generate the following code sequence:

LD  RO,  #a 

ADD RO,  RO,  SP

ADD RO,  RO,  i(SP)

LD  Rl,  b 

INC Rl   

ST  *R0,  Rl 

in the process of reducing the tree to a single node.       •

In order to implement the tree-reduction process in Example 8.18, we must address some issues related to tree-pattern matching:

  How is tree-pattern matching to be done? The efficiency of the code-generation process (at compile time) depends on the efficiency of the tree-matching algorithm.

• What do we do if more than one template matches at a given time? The efficiency of the generated code (at run time) may depend on the order in which templates are matched, since different match sequences will in general lead to different target-machine code sequences, some more efficient than others.

If no template matches, then the code-generation process blocks. At the other extreme, we need to guard against the possibility of a single node being rewritten indefinitely, generating an infinite sequence of register move instruc-tions or an infinite sequence of loads and stores.

To prevent blocking, we assume that each operator in the intermediate code can be implemented by one or more target-machine instructions. We further assume that there are enough registers to compute each tree node by itself. Then, no matter how the tree matching proceeds, the remaining tree can always be translated into target-machine instructions.

3. Pattern Matching by Parsing

Before considering general tree matching, we consider a specialized approach that uses an LR parser to do the pattern matching. The input tree can be treated as a string by using its prefix representation. For example, the prefix representation for the tree in Fig. 8.19 is

The tree-translation scheme can be converted into a syntax-directed trans-lation scheme by replacing the tree-rewriting rules with the productions of a context-free grammar in which the right sides are prefix representations of the instruction templates.

Example 8 . 2 1 :  The  syntax-directed translation scheme in  Fig.  8.21  is based on the tree-translation scheme in Fig. 8.20.      

The nonterminals  of the underlying grammar are R and  M.  The  terminal m represents a specific memory location, such as the location for the global variable b in Example 8.18. The production M m in Rule (10) can be thought of as matching M with m prior to using one of the templates involving M. Similarly, we introduce a terminal sp for register SP and add the production R S P . Finally, terminal c represents constants.

Using these terminals, the string for the input tree in Fig. 8.19 is

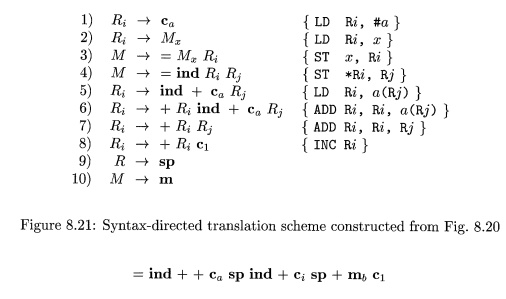
From the productions of the translation scheme we build an LR parser using one of the LR-parser construction techniques of Chapter 4. The target code is generated by emitting the machine instruction corresponding to each reduction.

A code-generation grammar is usually highly ambiguous, and some care needs to be given to how the parsing-action conflicts are resolved when the parser is constructed. In the absence of cost information, a general rule is to favor larger reductions over smaller ones. This means that in a reduce-reduce conflict,  the  longer reduction is  favored;  in  a shift-reduce  conflict,  the  shift move is chosen.  This  "maximal munch"  approach causes a larger number of operations to be performed with a single machine instruction.   There  are some  benefits  to  using LR  parsing in  code generation.  First, the parsing method is efficient and well  understood,  so reliable and  efficient code generators can be produced using the algorithms described in Chapter 4. Second, it is relatively easy to retarget the resulting code generator; a code selector for a new machine can be constructed by writing a grammar to describe the instructions of the new machine. Third, the quality of the code generated can be made efficient by adding special-case productions to take advantage of machine idioms.

However, there are some challenges as well. A left-to-right order of evalua-tion is fixed by the parsing method. Also, for some machines with large numbers of addressing modes, the machine-description grammar and resulting parser can become inordinately large. As a consequence, specialized techniques are neces-sary to encode and process the machine-description grammars. We must also be careful that the resulting parser does not block (has no next move) while parsing an expression tree, either because the grammar does not handle some operator patterns or because the parser has made the wrong resolution of some parsing-action conflict. We must also make sure the parser does not get into an infinite loop of reductions of productions with single symbols on the right side. The looping problem can be solved using a state-splitting technique at the time the parser tables are generated.

4. Routines for Semantic Checking

In a code-generation translation scheme, the same attributes appear as in an input tree, but often with restrictions on what values the subscripts can have. For example, a machine instruction may require that an attribute value fall in a certain range or that the values of two attributes be related.

These restrictions on attribute values can be specified as predicates that are invoked before a reduction is made. In fact, the general use of semantic actions and predicates can provide greater flexibility and ease of description than a purely grammatical specification of a code generator. Generic templates can be used to represent classes of instructions and the semantic actions can then be used to pick instructions for specific cases. For example, two forms of the addition instruction can be represented with one template:

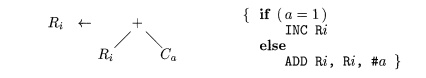
Parsing-action conflicts can be resolved by disambiguating predicates that can allow different selection strategies to be used in different contexts. A smaller description of a target machine is possible because certain aspects of the machine architecture, such as addressing modes, can be factored into the attributes. The complication in this approach is that it may become difficult to verify the accuracy of the translation scheme as a faithful description of the target machine, although this problem is shared to some degree by all code generators.

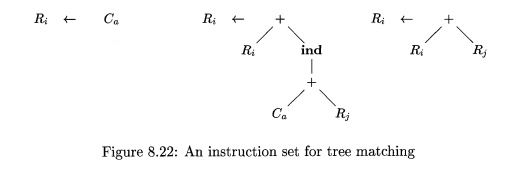
5. General Tree Matching

The LR-parsing approach to pattern matching based on prefix representations favors the left operand of a binary operator. In a prefix representation op E1 E₂, the limited-lookahead LR parsing decisions must be made on the basis of some prefix of Ei, since E1 can be arbitrarily long. Thus, pattern matching can miss nuances of the target-instruction set that are due to right operands.

Instead prefix representation, we could use a postfix representation. But, then an LR-parsing approach to pattern matching would favor the right oper-and.

For a hand-written code generator, we can use tree templates, as in Fig. 8.20, as a guide and write an ad-hoc matcher. For example, if the root of the input tree is labeled ind, then the only pattern that could match is for rule (5); otherwise, if the root is labeled +, then the patterns that could match are for rules (6-8).

For a code-generator generator, we need a general tree-matching algorithm. An efficient top-down algorithm can be developed by extending the string-pattern-matching techniques of Chapter 3. The idea is to represent each tem-plate as a set of strings, where a string corresponds to a path from the root to a leaf in the template. We treat all operands equally by including the position number of a child, from left to right, in the strings.

Example 8 . 2 2 : In building the set of strings for an instruction set, we shall drop the subscripts, since pattern matching is based on the attributes alone, not on their values.

The templates in Fig. 8.22 have the following set of strings from the root to a leaf:

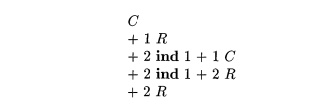
The string C represents the template with C at the root. The string +1R represents the + and its left operand R in the two templates that have + at the root.

Using sets of strings as in Example 8.22, a tree-pattern matcher can be constructed by using techniques for efficiently matching multiple strings in parallel.

In practice, the tree-rewriting process can be implemented by running the tree-pattern matcher during a depth-first traversal of the input tree and per-forming the reductions as the nodes are visited for the last time.

Instruction costs can be taken into account by associating with each tree-rewriting rule the cost of the sequence of machine instructions generated if that rule is applied. In Section 8.11, we discuss a dynamic programming algorithm that can be used in conjunction with tree-pattern matching.

By running the dynamic programming algorithm concurrently, we can select an optimal sequence of matches using the cost information associated with each rule. We may need to defer deciding upon a match until the cost of all alternatives is known. Using this approach, a small, efficient code generator can be constructed quickly from a tree-rewriting scheme. Moreover, the dynamic programming algorithm frees the code-generator designer from having to resolve conflicting matches or decide upon an order for the evaluation.

6. Exercises for Section 8.9

Exercise 8.9.1: Construct syntax trees for each of the following statements assuming all nonconstant operands are in memory locations:

a ) x =  a * b + c * d ;

b)  x [ i ]         =  y [ j ]    *  z [ k ] ;

c)  x  = x +  1;

Use the tree-rewriting scheme in Fig. 8.20 to generate code for each statement.

Exercise 8.9.2 : Repeat Exercise 8.9.1 above using the syntax-directed trans-lation scheme in Fig. 8.21 in place of the tree-rewriting scheme.

  Exercise 8.9.3: Extend the tree-rewriting scheme in Fig. 8.20 to apply to while- st at ement s.

   Exercise 8.9.4: How would you extend tree rewriting to apply to DAG's?