Railway Engineering:Transition Curve

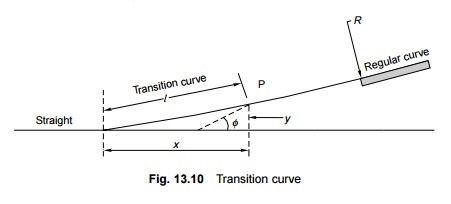
Transition Curve

As soon as a train commences motion on a circular curve from a straight line track, it is subjected to a sudden centrifugal force, which not only causes discomfort to the passengers but also distorts the track alignment and affects the stability of the rolling stock. In order to smoothen the shift from the straight line to the curve, transition curves are provided on either side of the circular curve so that the centrifugal force is built up gradually as the superelevation slowly runs out at a uniform rate (Fig. 13.10). A transition curve is, therefore, the cure for an uncomfortable ride, in which the degree of the curvature and the gain of superelevation are uniform throughout its length, starting from zero at the tangent point to the specified value at the circular curve. The following are the objectives of a transition curve.

(a)  To decrease the radius of the curvature gradually in a planned way from infinity at the straight line to the specified value of the radius of a circular curve in order to help the vehicle negotiate the curve smoothly.

(b) To provide a gradual increase of the superelevation starting from zero at the straight line to the desired superelevation at the circular curve.

(c)  To ensure a gradual increase or decrease of centrifugal forces so as to enable the vehicles to negotiate a curve smoothly.

1 Requirements of an Ideal Transition Curve

The transition curve should satisfy the following conditions.

(a)  It should be tangential to the straight line of the track, i.e., it should start from the straight part of the track with a zero curvature.

(b) It should join the circular curve tangentially, i.e., it should finally have the same curvature as that of the circular curve.

(c)  Its curvature should increase at the same rate as the superelevation.

(d) The length of the transition curve should be adequate to attain the final superelevation, which increases gradually at a specified rate.

2 Types of Transition Curves

The types of transition curves that can be theoretically provided are described here. The shapes of these curves are illustrated in Fig. 13.11.

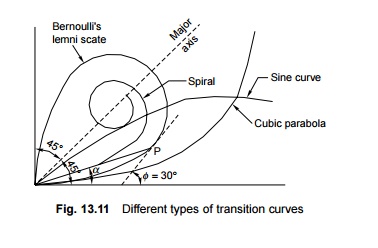
Euler's spiral       This is an ideal transition curve, but is not preferred due to mathematical complications. The equation for Euler's sprial is

Cubical spiral      This is also a good transition curve, but quite difficult to set on the field.                                      

Bernoulli's lemniscate In this curve, the radius decreases as the length increases and this causes the radial acceleration to keep on falling. The fall is, however, not uniform beyond a 30 o deflection angle. This curve is not used on railways.

Cubic parabola Indian Railways mostly uses the cubic parabola for transition curves. The equation of the cubic parabola is

In this curve, both the curvature and the cant increase at a linear rate. The cant of the transition curve from the straight to the curved track is so arranged that the inner rail continues to be at the same level while the outer rail is raised in the linear form throughtout the length of the curve. A straight line ramp is provided for such transition curves.

The notations used in Eqns (13.13) to (13.15) are as follows: f is the angle between the straight line track and the tangent to the transition curve, l is the distance of any point on the transition curve from the take-off point, L is the length of the transition curve, x is the horizontal coordinate on the transition curve, y is the vertical coordinate on the transition curve, and R is the radius of the circular curve.

S-shaped transition curve In an S-shaped transition curve, the curvature and superelevation assume the shape of two quadratic parabolas. Instead of a straight line ramp, an S-type parabola ramp is provided with this transition curve. The special feature of this curve is that the shift required ('shift' is explained in the following section) in this case is only half of the normal shift provided for a straight line ramp. The value of shift is

Further, the gradient is at the centre and is twice steeper than in the case of a straight line ramp. This curve is desirable in special conditions-when the shift is restricted due to site conditions.

The Railway Board has decided that on Indian Railways, transition curves will normally be laid in the shape of a cubic parabola.

3 Shift

For the main circular curve to fit in the transition curve, which is laid in the shape of a cubic parabola, it is required be moved inward by a measure known as the 'shift' (Fig. 13.12). The value of shift can be calculated using the formula

where S is the shift in m, L is the length of the transition curve in m, and R is the radius in m.

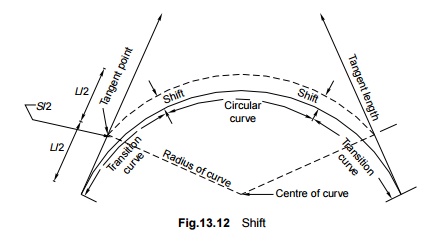
The offset (in centimetres) from the straight line to any point on the transition curve is calculated using the equation.

y = 16.7 x²/LR

where y is the offest from the staight line in cm, x is the distance from the commencement of the curve in m, L is the length of transition in m, and R is the radius of curve in m.

4 Length of Transition Curve

The length of the transition curve prescribed on Indian Railways is the maximum of the following three values:

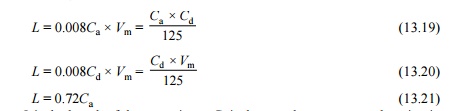
where L is the length of the curve in m, C_a is the actual cant or superelevation in mm, and C_d is the cant deficiency in mm.

Formulae (13.19) and (13.20) are based on a rate of change of a cant or cant deficiency of 35 mm/sec. Formula (13.21) is based on a maximum cant gradient of 1 in a 720 or 1.4 mm/m.

Other provisions made to meet the requirements of special situations are as follows.

(a)  When deciding the length of transition curves, particularly on high-speed routes, future speeds expected to be implemented on those tracks, such as 160 km/h for group A routes and 130 km/h for group B routes, may be taken into account.

(b) In exceptional cases, when there is no space available for providing full length transition curves, particularly on high-speed routes as per the preceding calculations, the length of the transition curve may be reduced to two-thirds of the desirable length as worked out by Eqns (13.19) and (13.20). This is based on the assumption that the rate of change of cant or cant deficiency will not exceed 55 mm/sec and the maximum cant gradient will not be steeper than 1 in 360 or 2.8 mm/m. This relaxation is permitted only for BG sections. For MG and NG sections, however, the cant gradient should not be steeper than 1 in 720 or 1.4 mm/h. For MG sections, the change of cant or cant deficiency should not exceed 35 mm/sec.

(c)  At locations where the length of the transition curve is restricted and as such may be inadequate to permit the maximum speed calculated for the circular curve, the design should be such that both the cant and the cant deficiency are lowered, which will reduce the maximum speed on the transition curve to permit the highest speed on the curve as a whole.

Example 13.6 A curve of 600 m radius on a BG section has a limited transition of 40 m length. Calculate the maximum permissible speed and superelevation for the same. The maximum sectional speed (MSS) is 100 km/h.

Solution In a normal situation, a curve of a 600 m radius will have quite a long transition curve for an MSS of 100 km/h. However, as the transition curve has been restricted to 40 m, the cant should be so selected that the speed on the main circular curve is equal to the speed on the transition curve as a whole.

5 Laying a Transition Curve

A transition curve is laid in the following steps (Fig. 13.13).

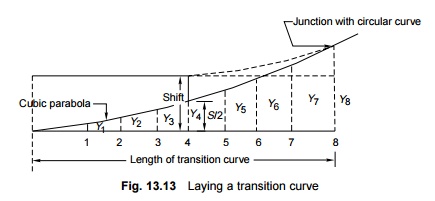
1.  The length of the transition curve is calculated by the formulae given in Eqns (13.19) to (13.21).

2.  This transition length is divided into an even number of equal parts, usually eight.

3.  The equations for a cubic parabola and the shift [Eqns (13.15) and (13.17)], reproduced here, are used for calculations.

4.  The shift is calculated using Formula (ii).

5.  The ordinates are then calculated at points 1, 2, 3, etc. using Formula (i).

6.  The point at which the transition curve starts is then determined approximately by shifting the existing tangent point backwards by distance equal to half the length of the transition curve.

7.  The offsets y₁, y₂, y₃, etc. are measured perpendicular to the tangent to get the profile of the transition curve.