Railway Engineering: Realignment of Curves

Realignment of Curves

A rail curve is likely to get distorted from its original alignment with the passage of time due to the following reasons.

(a)  Unbalanced loading on both the inner and outer rails due to cant excess at slower speeds or cant deficiency at higher speeds instead of the equilibrium speed for which the cant has been provided.

(b) Effect of large horizontal forces exerted on the rails by passing trains. These forces tend to make a curve flatter at certain locations and sharper at others and the radius of the curve thus varies from place to place. These result in a rough ride on the curve due to the change in the radial acceleration from place to place. Realignment of the curve, therefore, becomes necessary to restore the smooth running of vehicles on these curves.

1 Criteria for Realignment of Curves

The Indian Railway Way Manual and the Indian Railway Works Manual had earlier prescribed that a curve should be realigned when, during an inspection, the running on a curve is found to be unsatisfactory. No hard and fast rule was laid as to when a curve should be realigned. Subsequently, the Railway Board prescribed the following criteria for the realignment of a curve.

Cumulative frequency diagram

For group A and B routes, the need for curve realignment should be determined by drawing a cumulative frequency diagram showing the variation of the field versine over the theoretical versine. The versine variations measured on a 20-m chord should be limited to 4 mm and 5 mm for group A and B lines, respectively. Realignment should be taken up when the cumulative percentage of the versines lying within these limits is less than 80.

Station-to-station versine difference

The type of ride over a curve depends not only on the difference between the actual and the proposed versine but also on the station-to-station variation of the actual versine values. The station-to-station variation of versine determines the rate of change of radial acceleration, on which the comfort of the ride would depends. The following stipulations have been made regarding the different gauges adopted on the Indian Railways.

Broad gauge On curves where speeds in excess of 100 km/h are permitted, the station-to-station variation of versines at stations 10 m apart should not exceed 15 mm, and for speeds of 100 km/h and less, these variations should not exceed 20 mm or 20% of the average versine of the circular portion, whichever is more.

Metre gauge On curves which permit speeds in excess of 75 km/h, the station-to-station variation the versine at stations 10 m apart should not exceed l5 mm. For speeds of 75 km/h and less, such variations should not exceed 20 mm or 20% of the average versine of the circular portion, whichever is more.

The decision to completely realign a curve should be taken after ascertaining the type of ride the curve provides, on the basis of the cumulative frequency diagram or the distribution of the variation of versines between stations as described here.

Curve realignment can also be taken up under the following circumstances.

Unsatisfactory running of track

For other routes, curve realignment should be taken up when a curve is found to be unsatisfactory as a result of inspection done by trolley, from the footplate of the locomotive, by rear carriage, or as a result of various track tests that may have been carried out.

Local adjustment

When there is an abrupt variation of versines between adjacent stations, local adjustments should be done to achieve a versine variation which is within reasonable limits. Such corrections should be carried out before complete curve realignment is taken up.

2 String Lining Method of Realignment of Curves

The realignment of existing curves using a theodolite is difficult and laborious work. Therefore, curves are realigned by measuring the versines with the help of a string and then correcting these versines. This method is known as the string lining method on Indian Railways. It is based on the following basic principles.

(a)  The sum of all versines taken on equal chords of any two curves between the same tangents are equal. It follows that the final value of the sum of the differences between the existing and proposed versine must be zero.

(b) The throw at any station is equal to twice the second summation of the differences of the proposed and existing versine up to the previous station.

Procedure

Realigning a curve using the string lining method consists of the following three operations.

1.  Survey of the existing curve for measurement of versines.

2.  Computation of slews, including provision of proper transition and superelevation for the revised alignment.

3.  Slewing of the curve to the revised alignment.

Survey of existing curves

Existing curves are surveyed as follows.

(a)  Versine readings are taken on the gauge face of the outer rail of the curve at 10-m intervals, using 20-m chords.

(b) Versine readings are taken with the help of a nylon fishing cord. The cord is kept tight and at a preferred distance of 20 mm away from the gauge face side of the outer rail, with the help of a special gadget.

(c)  Versine readings should be taken for at least six stations beyond the apparent tangent point.

Computation of slews

Slews are computed as follows.

1.  The length of the transition curve is determined based on the permissible speed and degree of curvature as per standard practice. The versine gradient, i.e., the rate of change of versine per unit length, is then calculated once the length of the transition curve and the theoretical versine proposed to be adopted are known. After calculating the versine gradient, the versines proposed to be adopted for the transition length can be easily computed.

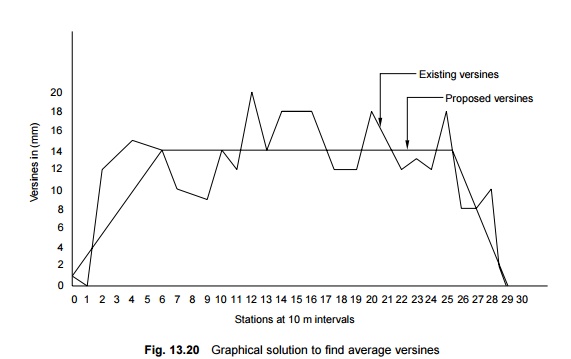
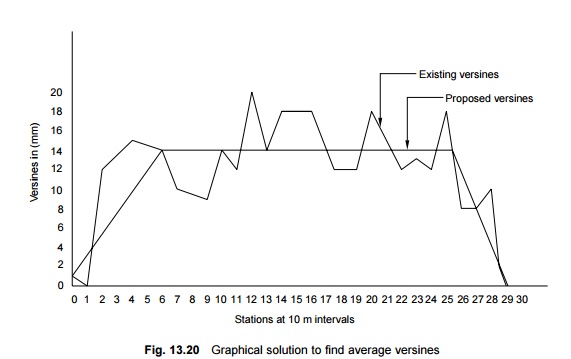
2.  The theoretical ideal versine proposed to be adopted for the transition length is calculated either exactly by detailed mathematical calculations or approximately by geometrical methods. In the geometrical method, the versines are plotted on a graph with respect to the number of stations and an average figure of versines is estimated by drawing a mean line in between the peaks and depressions of the graph as shown in Fig. 13.20.

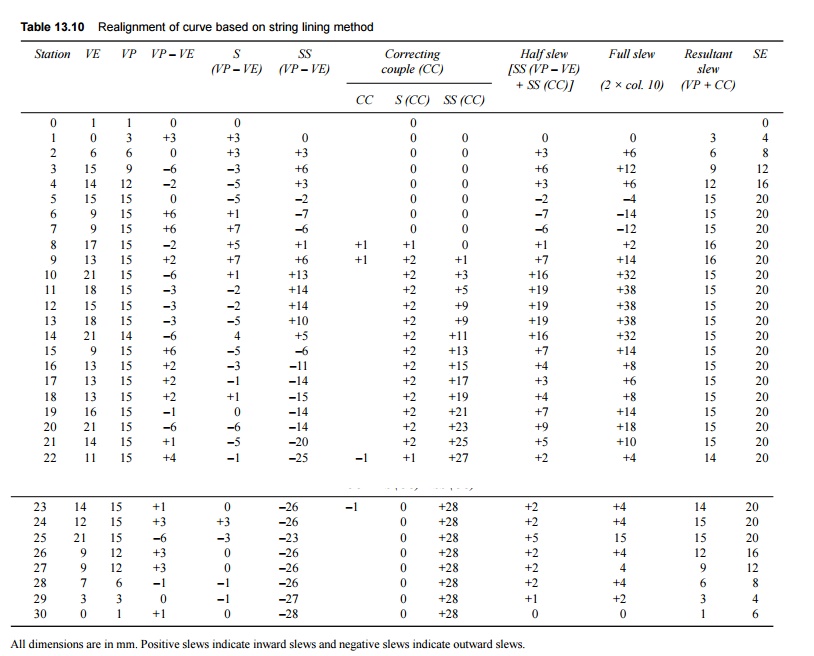
3.  A tabular statement is then prepared as shown in Table 13.10. In this table, the station numbers and existing versines (VE) are given in columns 1 and 2. The versines proposed to be adopted (VP) for the circular curve as well as for the transition length, as calculated before, are given in column three. It should be ensured that the sums of the proposed and existing versines are equal.

4.  Versine differences between the existing and proposed versines (VP - VE) are then calculated for each station and given in column 6, shifting it by half the station.

5.  The first summation of the versine difference is S(VP - VE) written in column 5 and in between, shifting is done by half the station, i.e., nth row of column 5 + (n + 1)th row of column 4 = (n + 1)th row of column 5-this must be zero in the end.

6.  The second summation of versines SS(VP - VE) is calculated by adding to it the first summation of versine difference. This is written in column 6, shifting it by half the station again. It should be ensured that the second summation of the difference of versines, which is also equal to half the slew, is zero at the first and last stations and at obligatory points, if any. If this condition is not satisfied, correcting couples are applied as described next.

7.  The correcting couples (CC) are applied (column 7) by changing the proposed versines in such a way that this brings down the second summation of the difference of versines at one place and makes the second summation negative at another place, keeping a proper distance, i.e., the correct number of stations, in between.

The first and second summations of the correcting couples, S(CC) and SS(CC), are given is done in columns 8 and 9, respectively. The correcting couple is applied depending upon the value of the second summation of versine difference derived against the last station, so that the final value, after adding the effect of the couple, becomes zero. Similarly, correcting couples are applied to control the slews at obligatory points. Otherwise too, slews must be limited to the minimum possible values in the entire curve.

8.  The resultant half slews (column 6 + column 9) and full slews (2 × columns 10) are shown in columns 10 and 11. The final versines (column 3 + column 7) to be adopted are written in column 12.

9.  The value of cant to be provided, rate of introduction of cant, and points of zero and maximum cant are also calculated. These are shown in column 13.

Slewing curve to the new alignment

The following points should be kept in mind when a curve is slewed to the new alignment.

(a)  A positive slew indicates an inward slew and a negative slew indicates an outward slew.

(b) The curve should be slewed to an accuracy of ±2 mm. After the realignment, the versine of the new curve should be measured for uniformity.

(c)  The necessary superelevation, which is already determined, should be given to the curve. The superelevation is zero at the tangent point.

(d) Curve indication posts should be fixed at important locations for checks to be carried out during maintenance, if required.

Use of computers for calculation of slew

As the normal method for calculating slew is slow and tedious, computerizing the same would be well appreciated. Eastern Railways has already developed two

programs on the IBM 1401 computer, one for calculating slews for simple curves and the other for calculating the same for compound curves with obligatory points so as to obtain solutions for curve realignment. The time taken is computing a realignment solutions for a curve with 150 stations is about 1.5 minutes. Besides saving time, computerized calculations provide much better precision.

3 Curve Correctors Cum Recorders

Indian Railways has procured about 50 curve correctors which continuously record the versines of curves and help in improving their alignments. The utility of this equipment increases if it can also be used for measuring gauge variations and unevenness, and this can be done easily by making suitable modifications to it. Accordingly, the RDSO has developed special attachments to be used with existing curve correctors for recording the unevenness and gauge parameters, thus converting the existing curve correctors into track recorder cum curve correctors. This new equipment measures the following:

(a)  Alignment over a 10-m chord

(b) Unevenness over a 10-m chord

(c)  Sleeper-to-sleeper gauge variation

4 Realignment of Curves on Double or Multiple Lines

On double or multiple tracks, each curve should be string lined independently. No attempt should be made to realign a curve by slewing it to a uniform centre-to-centre distance from another realigned curve due to the following reasons:

(a)  The existing track centres may not be uniform, and a relatively small throw on one track may entail a much larger (even prohibitively larger) throw on the adjacent track.

(b) It is nearly impossible to measure the centre-to-centre distance of curved tracks along the true radial line, and a small error in the angular direction of measurement would mean an appreciable error in the true radial distance.

(c)  The transition lengths at the entry and exit may measure differently, which make it impracticable to maintain uniform centres on them, even though the degree of the circular curves is nearly the same.