Railway Engineering: Safe Speed on Curves

Safe Speed on Curves

For all practical purposes safe speed means a speed which protects a carriage from the danger of overturning and derailment and provides a certain margin of safety. Earlier it was calculated empirically by applying Martin's formula:

For BG and MG

Transitioned curves

Indian Railways no longer follows this concept of safe speed on curves or the stipulations given here.

1.New Formula for Determining Maximum Permissible Speed on Transitioned Curves

Earlier, Martin's formula was used to work out the maximum permissible speed or safe speed on curves. This empirical formula has been changed by applying a formula based on theoretical considerations as per the recommendations of the committee of directors, chief engineers, and the ACRS. The maximum speed for transitioned curves is now determined as per the revised formulae given below.

On Broad Gauge

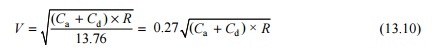
where V is the maximum speed in km/h, C_a is the actual cant in mm, C_d is the permitted cant deficiency in mm, and R is the radius in m. This equation is derived from Eqn (13.6) for equilibrium superelevation and is based on the assumption that G = 1750 mm, which is the centre-to-centre distance between the rail heads of a BG track with 52-kg rails.

On Metre Gauge

This is based on the assumption that the centre-to-centre (c/c) distance between the rail heads of an MG track is 1058 mm.

Narrow Gauge (762 min.)

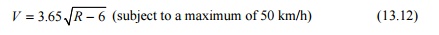
2.New Criteria for Determining Maximum Speed on Curves Without Transition

As per the procedure being followed at present, the determination of the maximum permissible speed on curves without transitions involves the concept of virtual transitions. The linear velocity of a train moving with uniform velocity on a straight track begins to change into angular velocity as soon as the first bogie reaches the tangent point. This change continues till the rear bogie reaches the tangent point, at which moment the train acquires full angular velocity. The change in the motion of the train from a straight line to a curve takes place over the shortest distance between the bogie centres and is considered a virtual transition. Normally, this distance is l4.6 m on BG, 13.7 m on MG, and 10.3 m on NG, commencing on a straight line at half the distance before the tangent point and terminating on the curve at half the distance beyond the tangent point. The deficiency of cant is considered as being gained over the length of the virtual transition and the cant has to be gained in a similar manner. The cant gradient must not be steeper than 1 in 360 on BG and 1 in 720 on MG and NG under any circumstance.

The safe speed should be worked out on the basis of the the cant that can be practically provided based on these criteria, and increased by the permissible amount of cant deficiency. In the case of non-transitioned curves, where no cant is provided, the safe speed for the curve can be worked out by calculating the permissible cant deficiency after taking into consideration the rate at which the cant deficincy is gained or lost over the virtual transition.

3 Maximum Permissible Speed on a Curve

The maximum permissible speed on a curve is the minimum value of the speed that is calculated after determining the four different speed limits mentioned here. The first three speed limits are taken into account for the calculation of maximum permissible speed, particularly if the length of the transition curve can be increased. For high-speed routes, however, the fourth speed limit is also very important, as cases may arise when the length of the transition curve cannot be altered easily.

(i)  Maximum sanctioned speed of the section This is the maximum permissible speed authorized by the commissioner of railway safety. This is determined after an analysis of the condition of the track, the standard of interlocking, the type of locomotive and rolling stock used, and other such factors.

(ii) Maximum speed of the section taking into consideration cant deficiency

This is the speed calculated using the formula given in Table 13.5. First, the

equilibrium speed is decided after taking various factors into consideration and the equilibrium superelevation (C_a) calculated. The cant deficiency (C_d) is then added to the equilibrium superelevation and the maximum speed is calculated as per this increased superelevalion (C_a + C_d).

Table 13.5   Calculation of permissible speed on curves

(iii) Maximum speed taking into consideration speed of goods train and cant excess Cant (C_a) is calculated based on the speed of slow moving traffic, i.e., goods train. This speed is decided for each section after taking various factors into

account, but generally its value is 65 km/h for BG and 50 km/h for MG.

The maximum value of cant excess (C_e) is added to this cant and it should be ensured that the cant for the maximum speed does not exceed the value of the sum of the actual cant + and the cant excess (C_a + C_e).

(iv) Speed corresponding to the length of the transition curves This is the least value of speed calculated after taking into consideration the various lenths of transition curves given by the formulae listed in Table 13.6.

The following points may be noted when calculating the maximum permissible speed on a curve.

(a)  Criterion (iv) is to be used only in cases where the length of the transition curve cannot be increased due to site restrictions. The rate of change of cant or cant deficiency has been permitted at a rate of 55 mm/sec purely as an interim measure for the existing curves on BG tracks.

(b) For high-speed BG routes, when the speed is restricted as a result of the rate of change of cant deficiency exceeding 55 mm/sec, it is necessary to limit the cant deficiency to a value lower than 100 mm in such a way that optimum results are obtained. In this situation, the maximum permissible speed is determined for a cant deficiency less than 100 mm, but gives a higher value of the maximum permissible speed. This concept is further explained with the help of the following solved problems.

Table 13.6 Various lengths of transition curves to be considered when calculating speed

* Notation used in the table: C_a is the value of actual cant in mm, V_m is the maximurm permissible speed in km/h, and C_d is the cant deficiency in mm.

Example 13.1 Calculate the superelevation and the maximum permissible speed for a 2 o BG transitioned curve on a high-speed route with a maximum sanctioned speed of 110 km/h. The speed for calculating the equilibrium superelevation as decided by the chief engineer is 80 km/h and the booked speed of goods trains is 50 km/h.

Solution

Simplified method of calculating permissible cant and speed

Often a simplified method is used for calculating the permissible cant and the maximum permissible speed in the field. This simplified method is applicable to most cases except those involving very flat curves.

Step 1 Calculate the cant for the maximum sanctioned speed of the section, say, 110 km/h, using the standard formula C = GV ² /127R . This is C₁₁₀.

Step 2 Calculate the cant using the same standard formula as for the slowest traffic, i.e., for a goods train which may be running at, say, 50 km/h. This is C₅₀. To this add cant excess. This becomes C₅₀ + C_e.

Step 3 Calculate the cant for equilibrium speed (if decided) using the same standard formula. Let it be 80 km/h. This value is C₈₀.

Step 4 Adopt the lowest of the three values obtained from the preceding steps and that becomes the permissible cant (C_a). The three values are C₁₁₀, C₅₀ + C_e, and C₈₀. Step 5 Taking this cant value (C_a), add the cant deficiency and find the maximum permissible speed using the Eqn (13.10).

Example 13.2 Calculate the superelevation, maximum permissible speed, and transition length for a 3 o curve on a high-speed BG section with a maximum sanctioned speed of 110 km/h. Assume the equilibrium speed to be 80 km/h and the booked speed of the goods train to be 50 km/h.

Example 13.3 Calculate the maximum permissible speed on a curve of a high speed BG group A route having the following particulars: degree of the curve = 1 o , superelevation = 80 mm, length of transition curve = 120 m, maximum speed likely to be sanctioned for the section =160 km/h.

Example 13.4 Calculate the maximum permissible speed on a 1 o curve on a Rajdhani route with a maximum sanctioned speed of 130 km/h. The superelevation provided is 50 mm and the transition length is 60 m. The transition length of the curve cannot be increased due to the proximity of the yard.

Example 13.5 A BG branch line track takes off as a contrary flexure through a 1 in 12 turnout from a main line track of a 3 o curvature. Due to the turnout, the maximum permissible speed on the branch line is 30 km/h. Calculate the negative superelevation to be provided on the branch line track and the maximum permissible speed on the main line track (when it takes off from a straight track).