Railway Engineering: Superelevation

Superelevation

The following terms are frequently used in the design of horizontal curves.

Superelevation or cant Superelevation or cant (C_a) is the difference in height between the outer and the inner rail on a curve. It is provided by gradually lifting the outer rail above the level of the inner rail. The inner rail is taken as the reference rail and is normally maintained at its original level. The inner rail is also known as the gradient rail. The main functions of superelevation are the following.

(a)  To ensure a better distribution of load on both rails

(b) To reduce the wear and tear of the rails and rolling stock

(c)  To neutralize the effect of lateral forces

(d) To provide comfort to passengers

Equilibrium speed When the speed of a vehicle negotiating a curved track is such that the resultant force of the weight of the vehicle and of radial acceleration is perpendicular to the plane of the rails, the vehicle is not subjected to any unbalanced radial acceleration and is said to be in equilibrium. This particular speed is called the equilibrium speed. The equilibrium speed, as such, is the speed at which the effect of the centrifugal force is completely balanced by the cant provided.

Maximum permissible speed This is the highest speed permitted to a train on a curve taking into consideration the radius of curvature, actual cant, cant deficiency, cant excess, and the length of transition. On cruves where the maximum permissible speed is less than the maximum sectional speed of the section of the line, permanent speed restriction becomes necessary.

Cant deficiency Cant deficiency (C_d) occurs when a train travels around a curve at a speed higher than the equilibrium speed. It is the difference between the theoretical cant required for such high speeds and the actual cant provided.

Cant excess Cant excess (C_e) occurs when a train travels around a curve at a speed lower than the equilibrium speed. It is the difference between the actual cant provided and the theoretical cant required for such a low speed.

Cant gradient and cant deficiency gradient These indicate the increase or decrease in the cant or the deficiency of cant in a given length of transition. A gradient of 1 in 1000 means that a cant or a deficiency of cant of 1 mm is attained or lost in every 1000 mm of transition length.

Rate of change of cant or cant deficiency This is the rate at which cant deficiency increases while passing over the transition curve, e.g., a rate of 35 mm per second means that a vehicle will experience a change in cant or a cant deficiency of 35 mm in each second of travel over the transition when travelling at the maximum permissible speed.

1 Centrifugal Force on a Curved Track

A vehicle has a tendency to travel in a straight direction, which is tangential to the curve, even when it moves on a circular curve. As a result, the vehicle is subjected to a constant radial acceleration:

Radial acceleration = g = V²/R

where V is the velocity (metres per second) and R is the radius of curve (metres). This radial acceleration produces a centrifugal force which acts in a radial direction away from the centre. The value of the centrifugal force is given by the formula

Force = mass × acceleration F = m × ( V²/R)

= (W/g) × ( V²/R)

where F is the centrifugal force (tonnes), W is the weight of the vehicle (tonnes), V is the speed (metre/sec), g is the acceleration due to gravity (metre/sec²), and R is the radius of the curve (metres).

To counteract the effect of the centrifugal force, the outer rail of the curve is elevated with respect to the inner rail by an amount equal to the superelevation. A state of equilibrium is reached when both the wheels exert equal pressure on the rails and the superelevation is enough to bring the resultant of the centrifugal force and the force exerted by the weight of the vehicle at right angles to the plane of the top surface of the rails. In this state of equilibrium, the difference in the heights of the outer and inner rails of the curve known as equilibrium superelevation.

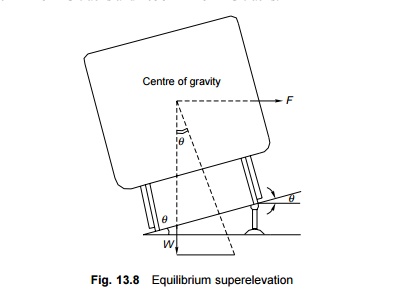
2 Equilibrium Superelevation

In Fig. 13.8, if q is the angle that the inclined plane makes with the horizontal line, then

where e is the equilibrium superelevation, G is the gauge, V is the velocity, g is the acceleration due to gravity, and R is the radius of the curve. In the metric system equilibrium superelevation is given by the formula

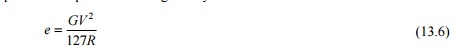
where e is the superelevation in millimetres, V is the speed in km/h, R is the radius of the curve in metres, and G is the dynamic gauge in millimetres, which is equal to the sum of the gauge and the width of the rail head in millimetres. This is equal to 1750 mm for BG tracks and 1058 mm for MG tracks.

3 Thumb Rules for Calculating Superelevation in the Field

A field engineer can adopt the following thumb rules for determining the superelevation of any curve.

(a)  Superelevation for BG in cm

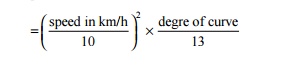
(b) For MG tracks the value of superelevation is taken as three-fifths of the value calculated using the preceding formula. The equilibrium speed is used in this formula.

For example, if the maximum sanctioned speed (MSS) of the section is 100 km/h, the equilibrium speed may be taken as 75% of the MSS, i.e., 75 km/h. The superelevation for a 1 o curve as calculated by the thumb rule is as follows:

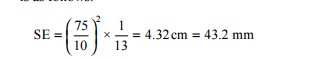
Note that presuming that the MSS is 100 km/h, the thumb rule is that for every 1 o of curve, the cant is approximately 43 mm for BG tracks and 25 mm for MG tracks.

4 Equilibrium Speed for Providing Superelevation

The amount of superelevation that is to be provided on a curve depends not only on the maximum speed of the fastest train, but also on the average speed of the goods traffic moving on that section. A compromise, therefore, has to be achieved by providing superelevation in a way that fast trains run smoothly without causing any discomfort to the passengers and slow trains run safely without fear of derailment due to excessive superelevation.

Earlier stipulations

Earlier the equilibrium speed prescribed on a level track under average conditions was as follows.

(a)  Where the maximum sanctioned speed of the section on both BG and MG tracks was over 50 km/h (30 mile/h), three-fourths of the maximum sanctioned speed of the section was taken as the equilibrium speed, subject to a choice between minimum speed of 50 km/h (30 mile/h) and the safe speed of the curve, whichever was less.

(b) Where the maximum sanctioned speed of the section on both BG and MG tracks was 50 km/h (30 mile/h) or less, the maximum sanctioned speed of the section or the safe speed of the curve, whichever was less, was taken as the equilibrium speed.

Revised standards

The standards for deriving the equilibrium speed stated in the preceding section have been revised by Indian Railways recently. As per the revised standards, the chief engineer (CE) should decide the equilibrium speed that would be required for the determination of the cant to be provided on a curve after careful deliberation and taking into consideration the following factors.

(a)  The maximum permissible speed which can actually be achieved both by fast trains and by goods trains

(b) Permanent and temporary speed restrictions

(c)  Number of stoppages

            Gradients

            Composition of both slow and fast trains

After deciding the equilibrium speed as described, the amount of superelevation to be provided is calculated using the following formula:

where e is the superelevation in mm, V is the speed in km/h, G is the dynamic gauge (1750 mm for BG and 1058 mm for MG tracks), and R is the radius of the curve in metres.

5 Maximum Value of Superelevation

The maximum value of superelevation has been laid down based on experiments carried out in Europe on a standard gauge for the overturning velocity, taking into consideration the track maintenance standards. The maximum value of the superelevation generally adopted around many railways around the world is 1/10th to 1/12th of the gauge. The values of maximum superelevation prescribed on Indian Railways are given in Table 13.2.

Table 13.2   Maximum value of superelvation

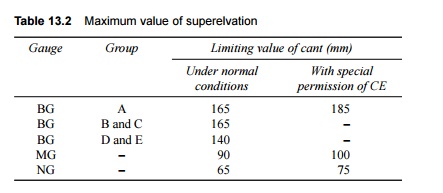
According to Table 13.2, a cant of 185 mm may be provided for the purpose of setting up permanent structures, etc. besides curves that have been laid on new construction sites and doublings on group A routes, which have the potential for allowing an increase in speed in the future. The transition length should also be provided on the basis of this cant of 185 mm for the purpose of planning and laying curves.

6 Cant Deficiency and Cant Excess

Cant deficiency is the difference between the equilibrium cant that is necessary for the maximum permissible speed on a curve and the actual cant provided. Cant deficiency is limited due to two considerations:

higher cant deficiency causes greater discomfort to passengers and

higher cant deficiency leads to greater unbalanced centrifugal forces, which in turn lead to the requirement of stonger tracks and fastenings to withstand the resultant greater lateral forces. The maximum values of cant deficiency prescribed for Indian Railways are given in Table 13.3.

Table 13.3   Allowable cant deficiency

The limiting values of cant excess have also been prescribed. Cant excess should not be more than 75 mm on broad gauge and 65 mm on metre gauge for all types of rolling stock. Cant excess should be worked out taking into consideration the booked speed of the trains running on a particular section. In the case of a section that carries predominantly goods traffic, cant excess should be kept low to minimize wear on the inner rail. Table 13.4 lists the limiting values of the various parameters that concern a curve.

Table 13.4   Limiting values of various parameters concerning curves

7 Negative Superelevation

When the main line lies on a curve and has a turnout of contrary flexure leading to a branch line, the superelevation necessary for the average speed of trains running over the main line curve cannot be provided. In Fig. 13.9, AB, which is the outer rail of the main line curve, must be higher than CD. For the branch line, however, CF should be higher than AE or point C should be higher than point A. These two contradictory conditions cannot be met within one layout. In such cases, the branch line curve has a negative superelevation and, therefore, speeds on both tracks must be restricted, particularly on the branch line.

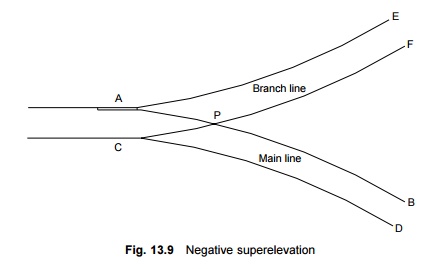
The provision of negative superelevation for the branch line and the reduction in speed over the main line can be calculated as follows.

(i)The equilibrium superelevation for the branch line curve is first calculated using the formula

(ii)  The equilibrium superelevation e is reduced by the permissible cant deficiency C_d and the resultant superelevation to be provided is

x = e -  C_d

where, x is the superelevation, e is the equilibrium superelevation, and C_d is 75 mm for BG and 50 mm for MG. The value of C_d is generally higher than that of e, and, therefore, x is normally negative. The branch line thus has a negative superelevation of x.

(iii)                       The maximum permissible speed on the main line, which has a superelevation of x, is then calculated by adding the allowable cant deficiency (x + C_d). The safe speed is also calculated and smaller of the two values is taken as the maximum permissible speed on the main line curve.