Railway Engineering: Vertical Curves

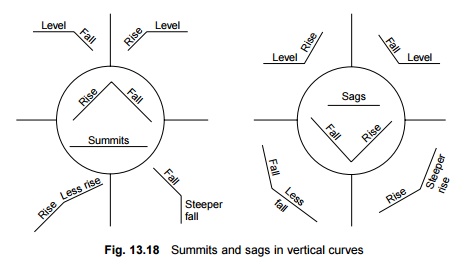
Vertical Curves

An angle is formed at the point where two different gradients meet, forming a summit or a sag as explained in Fig. 13.18. The angle formed at the point of contact of the gradients is smoothened by providing a curve called the vertical curve in the vertical plane. In the absence of a vertical curve, vehicles are likely to have a rough run on the track. Besides this, a change in the gradient may also cause bunching of vehicles in the sags and a variation in the tension of couplings in the summits, resulting in train parting and an uncomfortable ride. To avoid these ill effects, the change in gradient is smoothened by providing a vertical curve. A rising gradient is normally considered positive and a failing gradient is considered negative.

A vertical curve is normally designed as a circular curve. The circular profile en-sures a uniform rate of change of gradient, which controls the rotational acceleration.

1 Calculating the Length of a Vertical Curve (Old Method)

The length of a vertical curve depends upon the algebraic difference between the gradients and the type of curve formed (summit or sag). The rate of change of gradient in the case of summits should not exceed 0. 1% between successive 30.5-m (100-ft) chords, whereas the corresponding figure for sags is 0.05% per 30.5-m (100-ft) chord. The required length of a vertical curve for achieving the maximum permissible speed is given by the formula

L = (a/r) × 30.5 m (13.28) where L is the length of the vertical curve in m, a is the per cent algebraic difference between successive gradients, and r is the rate of change of the gradient, which is 0.1% for summit curves and 0.05% for sag curves.

2 Existing Provisions on Indian Railways

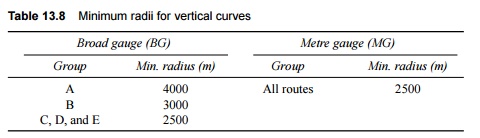
As per the existing provisions, vertical curves are provided only at the junction of gradients, when the alegebraic difference between the gradients is equal to or more than 0.4 per cent. The minimum radii for vertical curves are given in Table 13.8.

Table 13.8   Minimum radii for vertical curves

3 Setting a Vertical Curve

A vertical curve can be set by various methods, such as the tangent correction method and the chord deflection method. The tangent correction method, which is considered simpler than the other methods and is more convenient for the field staff, is described here (Fig. 13.19). It involves the following steps.

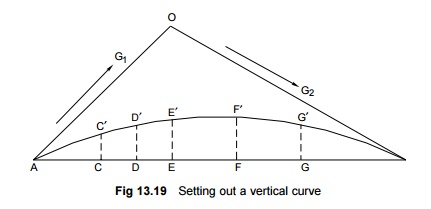
d reduced levels (RL) of the tangent points and apex are then worked out.

2.       Tangent corrections are then computed with the help of the following  equation:        

y = cx²        (13.29)

and C = g₁ - g₂ / 4.n

where y is the vertical ordinate, x is the horizontal distance from the springing point, g1 is gradient number 1 (positive for rising gradients), g2 is gradient number 2 (negative for falling gradients), and n is the number of chords up to half the length of the curve.

1.     The elevations of the stations on the curve are determined by algebrai adding the tangent corrections on tangent OA.

Example 13.9 Calculate the length of the vertical curve between two gradients meeting in a summit, one rising at a rate of 1 in 100 and the other falling at a rate of 1 in 200.

4 New Method of Calculating Length of Vertical Curve

According to the new method, the length of a vertical curve is calculated as follows: L = RQ   (13.30) where L is the length of the vertical curve, R is the radius of the vertical curve as

per the existing provisions given in Table 13.8, and Q is the difference in the percentage of gradients (expressed in radians).

It is seen that the length of the vertical curve calculated as per the new practice is relatively small compared to the length calculated using the old method. The length of the vertical curve according to the new practice is considered very reasonable for the purpose of laying the curve in the field, as can be seen from the next solved example.

Note that when the change in gradient (a) is positive it forms a summit and when it is negative it forms a sag.

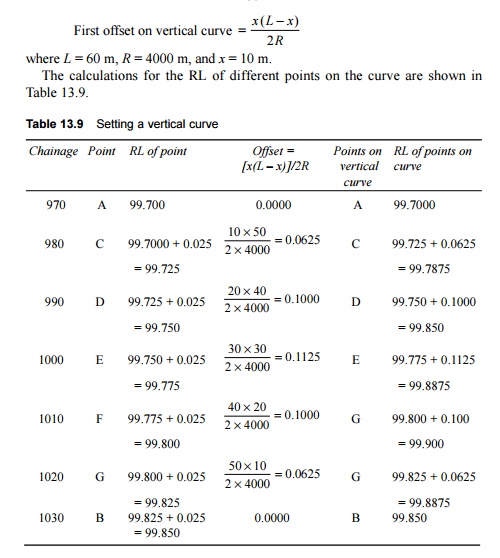
Example 13.10 A rising gradient of 1 in 100 meets a falling gradient of 1 in 200 on a group A route. The intersection point has a chainage of 1000 m and its RL is 100 m. Calculate the length of the vertical curve, and the RL and the chainage of the various points in order to set a vertical curve at this location.

Solution

First gradient = 1 in 100 (rising) = + 1% Second gradient = 1 in 200 (falling) = -0.5% Difference in gradient = (+ 1) - (-0.5) = 1.5% Length of vertical curve = L = RQ

= 4000 × (1.5/100) = 60 m Chainage of point A (refer Fig. 13.19) = 1000 - 30 = 970 m Chainage of point B = 1000 + 30 = 1030 m

RL of point A = 100 - (30/100) = 99.70 m RL of point B = 100 - (30/200) = 99.85 m

Increase in RL for 60 m = 99.85 - 99.70 = 0.15 m