Pseudorandom Number Generation Based on an Asymmetric Cipher

PSEUDORANDOM NUMBER GENERATION BASED ON AN ASYMMETRIC CIPHER

We noted in Chapter 7 that because a symmetric block cipher produces an apparently random output, it can serve as the basis of a pseudorandom number generator (PRNG). Similarly, an asymmetric encryption algorithm produces apparently random output and can be used to build a PRNG. Because asymmetric algorithms are typically much slower than symmetric algorithms, asymmetric algorithms are not used to generate open-ended PRNG bit streams. Rather, the asymmetric approach is useful for creating a pseudorandom function (PRF) for generating a short pseudorandom bit sequence.

In this section, we examine two PRNG designs based on pseudorandom functions.

PRNG Based on RSA

For a sufficient key length, the RSA algorithm is considered secure and is a good candidate to form the basis of a PRNG. Such a PRNG, known as the Micali-Schnorr PRNG [MICA91], is recommended in the ANSI standard X9.82 (Random Number Generation) and in the ISO standard 18031 (Random Bit   Generation).

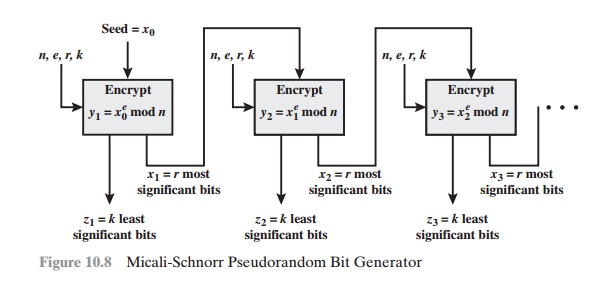
The PRNG is illustrated in Figure 10.8. As can be seen, this PRNG has much the same structure as the output feedback (OFB) mode used as a PRNG (see Figure 7.3b and the portion of Figure 6.6a enclosed with a dashed box). In this case, the encryption algorithm is RSA rather than a symmetric block cipher. Also, a portion of the output is fed back to the next iteration of the encryption algorithm and the remain- der of the output is used as pseudorandom bits. The motivation for this separation of the output into two distinct parts is so that the pseudorandom bits from one stage do not provide input to the next stage. This separation should contribute to forward unpredictability.

We can define the PRNG as follows.

The variable strength in requirement 4 is defined in NIST SP 800-90 as follows: A number associated with the amount of work (that is, the number of operations) required to break a cryptographic algorithm or system; a security strength is speci- fied in bits and is a specific value from the set (112, 128, 192, 256) for this Recommendation. The amount of work needed is 2strength.

There is clearly a tradeoff between r and k. Because RSA is computation- ally intensive compared to a block cipher, we would like to generate as many pseudorandom bits per iteration as possible and therefore would like a large value of k. However, for cryptographic strength, we would like r to be as large as possible.

For example, if e = 3 and N = 1024 , then we have the inequality 3r 7 1024, yielding a minimum required size for r of 683 bits. For r set to that size, k = 341 bits are generated for each exponentiation (each RSA encryption). In this case, each exponentiation requires only one modular squaring of a 683-bit number and one modular multiplication. That is, we need only calculate 1x_i * 1x_i mod n22mod n .

PRNG Based on Elliptic Curve Cryptography

In this subsection, we briefly summarize a technique developed by the U.S. National Security Agency (NSA) known as dual elliptic curve PRNG (DEC PRNG). This technique is recommended in NIST SP 800-90, the ANSI standard X9.82, and the ISO standard 18031. There has been some controversy regarding both the security and efficiency of this algorithm compared to other alternatives (e.g., see [SCHO06], [BROW07]).

[SCHO06] summarizes the algorithm as follows: Let P and Q be two known points on a given elliptic curve. The seed of the DEC PRNG is a random integer s0 Î {0, 1, ...... , #E(GF(p)) - 1}, where # E(GF(p)) denotes the number of points on the curve. Let x denote a function that gives the x-coordinate of a point of the curve. Let lsbi1s2 denote the i least significant bits of an integer s. The DEC PRNG trans- forms the seed into the pseudorandom sequence of length 240k, k > 0, as follows.

Given the security concerns expressed for this PRNG, the only motivation for its use would be that it is used in a system that already implements ECC but does not implement any other symmetric, asymmetric, or hash cryptographic algorithm that could be used to build a PRNG.