Chapter: Cryptography and Network Security Principles and Practice : Asymmetric Ciphers : Other Public-Key Cryptosystems
Elliptic Curve Arithmetic
ELLIPTIC CURVE
ARITHMETIC
Most of the products and standards that use
public-key cryptography for encryp- tion and digital signatures use RSA. As we
have seen, the key length for secure RSA use has increased
over recent years,
and this has put a heavier processing load on applications using RSA. This burden has ramifications, especially for electronic
commerce sites that conduct large numbers of secure transactions. A competing system challenges RSA: elliptic
curve cryptography (ECC).
ECC is showing up in standardization
efforts, including the
IEEE P1363 Standard for Public-Key
Cryptography.
The principal attraction of ECC, compared to RSA, is that it
appears to offer equal security for a far smaller key size, thereby
reducing processing overhead. On the other hand, although the theory of ECC has been around
for some time, it is only recently that products have begun to appear and that
there has been sustained
cryptanalytic interest in probing for weaknesses. Accordingly, the confidence level in
ECC is not yet as high as that in RSA.
ECC is fundamentally more difficult to
explain than either RSA or Diffie- Hellman, and
a full mathematical description is beyond the scope
of this book. This section and the next give some background on elliptic
curves and ECC. We begin with a
brief review of the concept of abelian group. Next, we examine the concept
of elliptic curves
defined over the real numbers.
This is followed
by a look at elliptic curves defined over finite fields. Finally, we
are able to examine elliptic curve ciphers.
The reader may wish to review the material on finite fields
in Chapter 4 before
proceeding.
Abelian Groups

A number of public-key ciphers are based on the use of an abelian group. For example, Diffie-Hellman key exchange involves multiplying pairs of nonzero inte- gers modulo a prime number q. Keys are generated by exponentiation over the group, with exponentiation defined as repeated multiplication. For example,

determine k given
a and ak; this is the
discrete logarithm problem.
For elliptic curve
cryptography, an operation over elliptic curves,
called addi- tion, is used. Multiplication is defined by repeated addition.
For example,
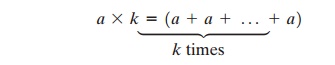
where the addition is performed over an elliptic curve. Cryptanalysis involves determining k given a and (a * k).
An elliptic
curve is defined by an equation
in two variables with coefficients. For cryptography, the variables and
coefficients are restricted to elements in a finite field, which results in the definition of a finite abelian group. Before looking at this, we first look at elliptic curves in
which the variables and coefficients are real numbers.
This case is perhaps easier to visualize.
Elliptic Curves
over Real Numbers
Elliptic curves are not ellipses. They are
so named because they are described by cubic
equations, similar to those used
for calculating the
circumference of an ellipse.
In general, cubic equations for elliptic curves take the following form, known
as a Weierstrass equation:
y2 + axy + by = x3
+ cx2
+ dx + e
where a, b, c, d, e are real numbers and x and y take
on values in the real numbers.4 For our purpose,
it is sufficient to limit
ourselves to equations of the form

Such equations are said to be cubic, or of degree 3, because the highest expo- nent they contain is a 3. Also included
in the definition of an elliptic curve is a single
element denoted O and called the
point
at infinity or the zero
point, which we discuss subsequently. To plot such a curve, we need to compute
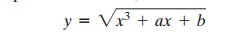
For given values
of a and b, the plot consists
of positive and negative values
of y for each value
of x. Thus, each curve
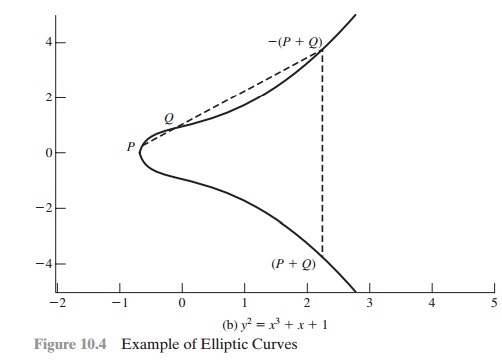
is symmetric about y = 0. Figure 10.4 shows
two examples of elliptic
curves. As you can see, the formula
sometimes produces weird- looking curves.
Now, consider the set of points E(a, b)
consisting of all of the points (x, y) that satisfy Equation (10.1) together
with the element O. Using a different
value of the pair (a, b) results in a different set E(a, b).
Using this terminology, the two curves in Figure 10.4 depict the sets E(-1, 0) and E(1, 1),
respectively.
GEOMETRIC DESCRIPTION OF ADDITION It can be shown that a group can be defined based on the
set E(a, b) for specific values of a and
b in Equation (10.1), provided the following condition is met:
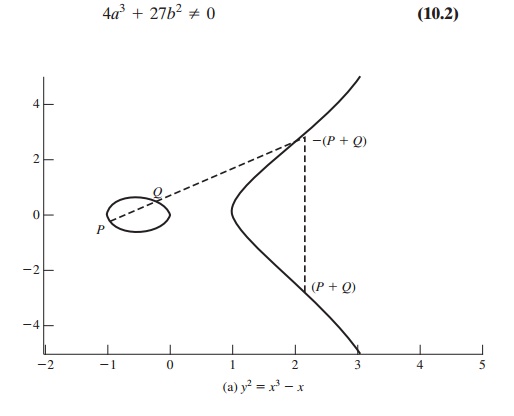
To define the group, we must define an operation, called addition and denoted by +,
for the set E(a, b), where a and b satisfy Equation (10.2). In geometric
terms, the rules for addition
can be stated as follows:
If three points
on an elliptic curve lie on
a straight line, their sum is O. From this definition, we can define the rules of addi- tion over an elliptic
curve.
1.
O serves as the additive identity. Thus
O
= -O; for any point P on
the elliptic curve, P + O = P. In what follows,
we assume P != O and Q != O.
The negative of a point P is the point with the same x coordinate but the negative
of the y coordinate; that is, if P = (x, y), then -P
= (x, -y). Note that these two points can be joined
by a vertical line. Note that P + (-P) = P - P = O.
1.
To
add two points P and Q with different x coordinates, draw a straight line
between them and find the third point of intersection R. It is easily seen that there
is a unique point R that
is the point of intersection (unless the line is tan-
gent to the curve at either P or
Q, in which case we take R = P or R = Q, respectively). To form a group structure, we need to
define addition on these three points: P + Q = -R. That is, we define P + Q to be the mirror image (with respect to the x axis) of the third point of intersection. Figure 10.4 illustrates
this construction.
2.
The geometric interpretation of the preceding
item also applies to two points, P and
-P, with the same x coordinate. The points are joined by a vertical line, which can be viewed as also intersecting the curve at the infinity
point. We there-
fore have P + (-P) = O, which is consistent
with item (2).
3.
To
double a point Q, draw the tangent line and find the other point of inter- section
S. Then Q + Q = 2Q = -S.
With the preceding list of rules, it can be
shown that the set E(a, b)
is an abelian group.
ALGEBRAIC
DESCRIPTION OF ADDITION In this subsection, we present some results that enable
calculation of additions over elliptic curves.5 For two distinct points, P = (xP , yP) and Q = (xQ,
yQ),
that are not negatives of each other, the slope of the line l that joins them is Δ = (yQ - yP)>(xQ - xP) . There is exactly
one other point where l intersects the elliptic curve,
and that is the negative
of the sum of P and
Q.
After some algebraic manipulation, we can
express the sum R = P + Q as

Elliptic Curves over Zp
Elliptic curve
cryptography makes use of elliptic curves
in which the variables and coefficients are all restricted to
elements of a finite field. Two families
of elliptic curves are used in cryptographic
applications: prime curves over Zp and
binary
curves over GF(2m). For a prime curve over
Zp, we use a cubic
equation in which
the
variables and coefficients all take on values in the set
of integers from 0 through
p - 1 and in which calculations are performed modulo
p. For a binary curve defined over GF(2m), the variables and coefficients all take on values in GF(2m) and in cal-
culations are performed over GF(2m). [FERN99] points
out that prime curves are best for software
applications, because the extended bit-fiddling operations needed by
binary curves are not required; and that binary curves are best for hardware
applications, where it takes remarkably few logic gates to create a powerful,
fast cryptosystem. We examine these two families
in this section and the next.
There is no obvious geometric interpretation
of elliptic curve arithmetic over
finite fields. The algebraic interpretation used for elliptic curve
arithmetic over real numbers does readily carry
over, and this is the approach we take.
For elliptic curves over Zp,
as with real numbers, we limit ourselves to equa- tions of the form of Equation
(10.1), but in this case with coefficients and variables
limited to Zp:
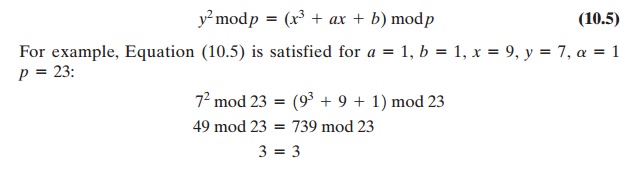
Now consider the set Ep(a, b) consisting of all pairs of integers (x, y)
that sat- isfy Equation (10.5), together with a point at infinity O. The coefficients a and b and the variables
x and y are all elements of Zp.
For example,
let p = 23 and consider the
elliptic curve y2
= x3 + x + 1.
In
this case, a = b = 1. Note that this equation is the same as that of Figure
10.4b. The figure shows a continuous curve with all of the real points that
satisfy the equation. For the set E23(1, 1), we are only interested in the nonnegative integers
in the quadrant from (0, 0) through (p - 1,
p - 1) that satisfy the equation mod
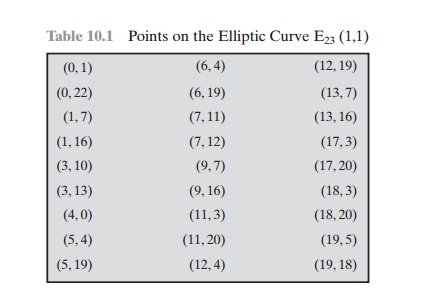
p. Table 10.1
lists the points (other than O) that
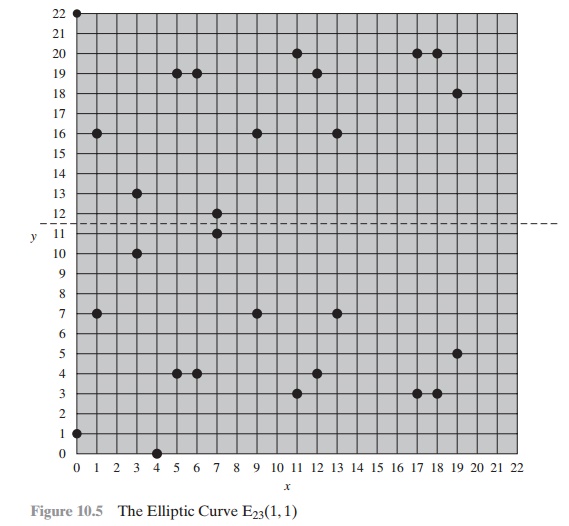
are part of E23(1, 1). Figure 10.5 plots the points
of E23(1, 1); note that the points,
with one exception, are symmetric about y = 11.5.
It can be shown that a finite abelian group
can be defined based on the set Ep(a, b)
provided that (x3 + ax + b) mod p has no repeated factors. This is
equiva- lent to the condition
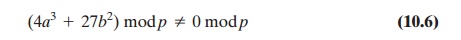
Note that Equation
(10.6) has the same form as Equation
(10.2).
The rules for addition over Ep(a, b), correspond to the algebraic
technique described for elliptic
curves defined over real numbers. For all points P, Q Î Ep(a, b):


The last step in the preceding equation
involves taking the multiplicative inverse of 4 in Z23. This can be done
using the extended Euclidean algorithm defined in Section 4.4. To confirm, note
that (6 * 4) mod 23
= 24
mod 23 = 1.
xR = (62 - 3 - 3) mod 23 = 30 mod 23 = 7
yR = (6(3 - 7) - 10) mod 23 = (-34) mod 23 = 12
and 2P = (7, 12).
For
determining the security of various elliptic curve ciphers, it is of some
inter- est to know the number of points in a finite abelian group defined over
an elliptic curve. In the case of the finite group EP(a, b), the number of
points N is bounded by
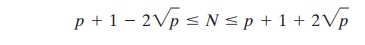
Note that the number of points in Ep(a, b) is approximately equal to the number of elements in Zp, namely
p
elements.
Elliptic Curves over GF(2m)
Recall from Chapter 4 that a finite field GF(2m) consists of 2m elements, together
with addition and multiplication operations that can be defined over
polynomials. For elliptic
curves over GF(2m), we use a cubic equation
in which the variables and coefficients all take on values in GF(2m) for some number m and
in which calcula- tions are performed using the rules of arithmetic in GF(2m).
It turns out that the form of cubic equation
appropriate for cryptographic appli- cations for elliptic curves is somewhat
different for GF(2m) than for Zp. The form is

where it is understood that the variables x and y and the coefficients a and
b are elements of GF(2m) and that calculations are performed in GF(2m).
Now consider
the set
E2m(a, b) consisting
of all
pairs of integers (x, y) that satisfy Equation (10.7), together with a point at
infinity O.
For example, let us use the finite field
GF(24) with the
irreducible polynomial f(x)
= x4 + x + 1. This yields a generator g that satisfies f(g)
= 0 with a value of g4 = g + 1
, or in binary, g = 0010.
We can develop the powers of g as
follows.

Table 10.2 lists the points (other than O) that are part of E241g4,
12 . Figure 10.6 plots the points of E241g4,
12 .
It can be shown that a finite abelian group
can be defined based on the set E2m(a, b), provided that b != 0. The rules for addition can be stated as follows.
For all points P, Q Î E2m(a, b):

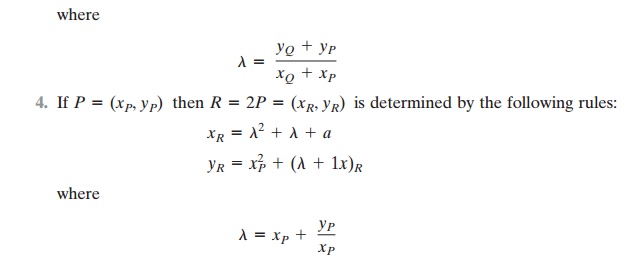
Related Topics