Elgamal Cryptographic System

ELGAMAL CRYPTOGRAPHIC SYSTEM

In 1984, T. Elgamal announced a public-key scheme based on discrete logarithms, closely related to the Diffie-Hellman technique [ELGA84, ELGA85]. The ElGamal2 cryptosystem is used in some form in a number of standards including the digital signature standard (DSS), which is covered in Chapter 13, and the S/MIME e-mail standard (Chapter 18).

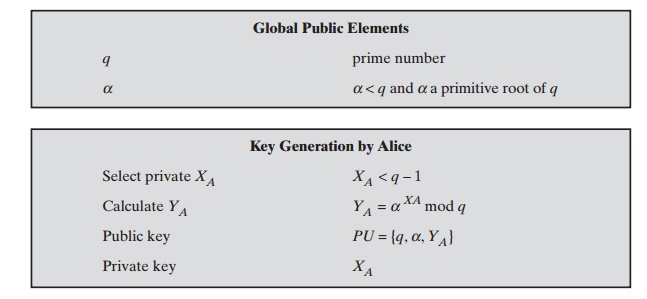
As with Diffie-Hellman, the global elements of ElGamal are a prime number q and a, which is a primitive root of q. User A generates a private/public key pair as follows:

1.                                                                               Generate a random integer XA, such that 1 6 XA 6 q - 1.

2.                                                                               Compute YA  =  aXA mod q .

3.                                                                               A’s private key is XA; A’s pubic key is {q, a, YA}.

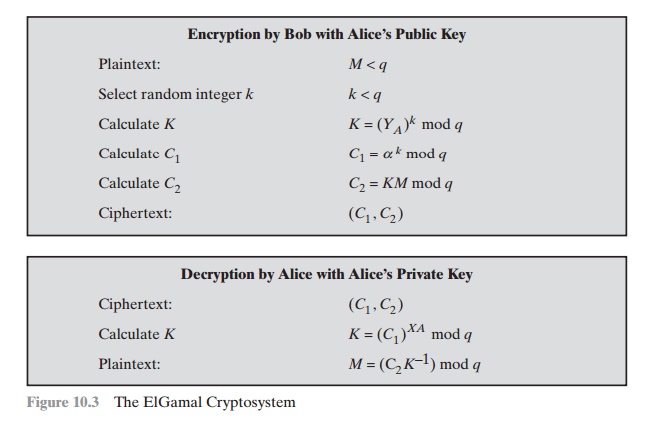
Any user B that has access to A’s public key can encrypt a message as  follows:

1.         Represent the message as an integer M in the range 0 … M … q - 1. Longer messages are sent as a sequence of blocks, with each block being an integer less than q.

2.         Choose a random integer k such that 1 … k … q - 1.

3.         Compute a one-time key K  = (YA)k mod q .

4.         Encrypt M as the pair of integers (C1, C2) where

C1 = ak mod q;  C2 = KM mod q

User A recovers the plaintext as follows:

1.                                                                               Recover the key by computing K  =  (C1)XA mod q .

2.                                                                               Compute M  = (C2K-1) mod q .

These steps are summarized in Figure 10.3. It corresponds to Figure 9.1a: Alice generates a public/private key pair; Bob encrypts using Alice’s public key; and Alice decrypts using her private key.

Let us demonstrate why the ElGamal scheme works. First, we show how K is recovered by the decryption process:

K  = (YA)k mod q                          K is defined during the encryption process

K  =  (aXA mod q)k mod q                 substitute using YA  =  aXA mod q K  =  akXA mod q        by the rules of modular arithmetic

K  =  (C1)XA mod q                               substitute using C1  =  ak mod q

Next, using K, we recover the plaintext as

C2  = KM mod q

(C2K-1) mod q  = KMK-1 mod q  = M mod q  = M

We can restate the ElGamal process as follows, using Figure 10.3.

1.                                       Bob generates a random integer k.

2.                                       Bob generates a one-time key K using Alice’s public-key components YA, q, and k.

3.                                       Bob encrypts k using the public-key component a, yielding C1. C1 provides suffi- cient information for Alice to recover K.

4.                                       Bob encrypts the plaintext message M using K.

5.                                       Alice recovers K from C1 using her private key.

6.                                       Alice uses K-1 to recover the plaintext message from C2.

Thus, K functions as a one-time key, used to encrypt and decrypt the message.

For example, let us start with the prime field GF(19); that is, q = 19. It has primitive roots {2, 3, 10, 13, 14, 15}, as shown in Table 8.3. We choose a = 10.

Alice generates a key pair as follows:

1.                                                 Alice chooses XA  = 5.

2.                                                 Then YA = a XA mod q = a5 mod 19 = 3 (see Table 8.3).

3.                                                 Alice’s private key is 5; Alice’s pubic key is {q, a, YA}   =  {19, 10, 3}.

Suppose Bob wants to send the message with the value M = 17. Then,

1.                                       Bob chooses k  = 6.

2.                                       Then K = (YA)k mod q = 36 mod 19 = 729 mod 19 = 7.

3.                                       So

C1  = ak mod q  = a6 mod 19 = 11

C2 = KM mod q  =  7  * 17 mod 19 = 119 mod 19 = 5

4.                                       Bob sends the ciphertext (11, 5). For decryption:

1.                                                                               Alice calculates K  =  (C1)XA mod q  =  115 mod 19 = 161051 mod 19 = 7.

2. Then K -1 in GF(19) is 7-1 mod 19 = 11.

3.  Finally, M = (C2K- 1) mod q = 5 * 11 mod 19 = 55 mod 19 = 17.

If a message must be broken up into blocks and sent as a sequence of encrypted blocks, a unique value of k should be used for each block. If k is used for more than one block, knowledge of one block m1 of the message enables the user to compute other blocks as follows. Let

The security of ElGamal is based on the difficulty of computing discrete logarithms. To recover A’s private key, an adversary would have to compute XA = dloga,q(YA) . Alternatively, to recover the one-time key K, an adversary would have to determine the random number k, and this would require comput- ing the discrete logarithm k = dloga,q(C1). [STIN06] points out that these calcu- lations are regarded as infeasible if p is at least 300 decimal digits and q - 1 has at least one “large” prime factor.