Elliptic Curve Cryptography

Consider  the  group E23(9,17).  This  is  the  group  defined  by  the   equation y2 mod 23 = (x3 + 9x + 17) mod 23 . What is the discrete logarithm k of Q = (4, 5) to the base P = (16, 5)? The brute-force method is to compute multiples of P until Q is found. Thus,

P  = (16, 5); 2P  = (20, 20); 3P  = (14, 14); 4P  = (19, 20); 5P  = (13, 10);

6P  = 17, 32; 7P  = 18, 72; 8P  = (12, 17); 9P  = (4, 5)

Because  9P = (4, 5) = Q, the  discrete  logarithm  Q = (4,  5) to  the base P = (16, 5) is k = 9. In a real application, k would be so large as to make the brute- force approach infeasible.

In the remainder of this section, we show two approaches to ECC that give the flavor of this technique.

Analog of Diffie-Hellman Key Exchange

Key exchange using elliptic curves can be done in the following manner. First pick a large integer q, which is either a prime number p or an integer of the form 2m, and elliptic curve parameters a and b for Equation (10.5) or Equation (10.7). This defines the elliptic group of points Eq(a, b). Next, pick a base point G = (x1, y1) in Ep(a, b) whose order is a very large value n. The order n of a point G on an elliptic curve is the smallest positive integer n such that nG = 0 and G are parameters of the cryptosystem known to all participants.

A key exchange between users A and B can be accomplished as follows (Figure 10.7).

1.         A selects an integer nA less than n. This is A’s private key. A then generates a public key PA  = nA * G; the public key is a point in Eq(a, b).

2.         B similarly selects a private key nB and computes a public key PB.

3.         A  generates  the  secret  key k = nA * PB.  B  generates  the  secret  key k = nB * PA.

The two calculations in step 3 produce the same result because

nA * PB = nA * (nB * G) = nB * (nA * G)    = nB * PA

To break this scheme, an attacker would need to be able to compute k given G

and kG, which is assumed to be hard.

As an example,6 take p  =  211; Ep(0, - 4), which is equivalent to the  curve

y2 = x3 - 4; and G  =  (2, 2). One can calculate that 240G  =  O. A’s private key is

nA  =  121,  so  A’s   public  key   is   PA  =  121(2, 2)  =  (115, 48).  B’s   private key

is nB  =  203, so B’s public key is 203(2, 3)  =  (130, 203). The shared secret key   is

121(130, 203)  =  203(115, 48)  =  (161, 69).

Note that the secret key is a pair of numbers. If this key is to be used as     a session key for conventional encryption, then a single number must be gener- ated. We could simply use the x coordinates or some simple function of the x coordinate.

Elliptic Curve Encryption/Decryption

Several approaches to encryption/decryption using elliptic curves have been ana- lyzed in the literature. In this subsection, we look at perhaps the simplest. The first task in this system is to encode the plaintext message m to be sent as an x–y point Pm. It is the point Pm that will be encrypted as a ciphertext and subsequently decrypted. Note that we cannot simply encode the message as the x or y coordinate of a point, because not all such coordinates are in Eq(a, b); for example, see Table

            Again, there are several approaches to this encoding, which we will    not

address here, but suffice it to say that there are relatively straightforward tech- niques that can be used.

As with the key exchange system, an encryption/decryption system requires a point G and an elliptic group Eq(a, b) as parameters. Each user A selects a private key nA and generates a public key PA  =  nA  * G.

To encrypt and send a message Pm to B, A chooses a random positive integer k

and produces the ciphertext Cm consisting of the pair of points:

Cm  =  {kG, Pm  + kPB}

Note that A has used B’s public key PB. To decrypt the ciphertext, B multiplies the first point in the pair by B’s secret key and subtracts the result from the second point:

Pm + kPB - nB(kG) = Pm + k(nBG) - nB(kG) =  Pm

A has masked the message Pm by adding kPB to it. Nobody but A knows the value of k, so even though Pb is a public key, nobody can remove the mask kPB. However, A also includes a “clue,” which is enough to remove the mask if one knows the private key nB. For an attacker to recover the message, the attacker would have to compute k given G and kG, which is assumed to be hard.

As  an  example of  the encryption process (taken from [KOBL94]), take  p = 751; Ep(-1, 188) , which is equivalent to the curve y2  = x3  - x  + 188; and  G = (0, 376). Suppose that A wishes to send a message to B that is encoded in the elliptic point Pm = (562, 201) and that A selects the random number k  = 386. B’s public  key  is PB  = (201, 5).  We   have 386(0, 376)  = (676, 558), and (562, 201) + 386(201, 5)  =  (385, 328). Thus, A sends the cipher text {(676, 558), (385,    328)}.

Security of Elliptic Curve  Cryptography

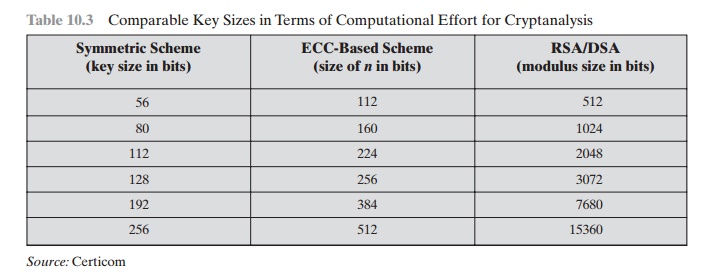
The security of ECC depends on how difficult it is to determine k given kP and P. This is referred to as the elliptic curve logarithm problem. The fastest known tech- nique for taking the elliptic curve logarithm is known as the Pollard rho method. Table 10.3 compares various algorithms by showing comparable key sizes in terms of computational effort for cryptanalysis. As can be seen, a considerably smaller key size can be used for ECC compared to RSA. Furthermore, for equal key lengths, the computational effort required for ECC and RSA is comparable [JURI97]. Thus, there is a computational advantage to using ECC with a shorter key length than a comparably secure RSA.

Table 10.3     Comparable Key Sizes in Terms of Computational Effort for  Cryptanalysis