Diffie-Hellman Key Exchange

DIFFIE-HELLMAN KEY EXCHANGE

The first published public-key algorithm appeared in the seminal paper by Diffie and Hellman that defined public-key cryptography [DIFF76b] and is generally referred to as Diffie-Hellman key exchange. A number of commercial products employ this key exchange technique.

The purpose of the algorithm is to enable two users to securely exchange a key that can then be used for subsequent encryption of messages. The algorithm itself is limited to the exchange of secret values.

The Diffie-Hellman algorithm depends for its effectiveness on the difficulty of computing discrete logarithms. Briefly, we can define the discrete logarithm in the following way. Recall from Chapter 8 that a primitive root of a prime number p as one whose powers modulo p generate all the integers from 1 to p - 1. That is, if a is a primitive root of the prime number p, then the numbers

a mod p, a2 mod p, Á , ap - 1 mod p

are distinct and consist of the integers from 1 through p - 1 in some permutation.

For any integer b and a primitive root a of prime number p, we can find a unique exponent i such that

b  K ai (mod p)       where 0 … i … (p -  1)

The exponent i is referred to as the discrete logarithm of b for the base a, mod p. We express this value as dloga,p(b). See Chapter 8 for an extended discussion of discrete logarithms.

The Algorithm

Figure 10.1 summarizes the Diffie-Hellman key exchange algorithm. For this scheme, there are two publicly known numbers: a prime number q and an integer a that is a primitive root of q. Suppose the users A and B wish to exchange a key. User A selects a random integer XA  6  q and computes YA  =  aXA mod q. Similarly, user B independently selects a random integer XB  6  q and computes YB  =  aXB mod q. Each side keeps the X value private and makes the Y value available publicly to the other side. User A computes the key as K  =  (YB)XA mod q  and user B computes the key as K  =  (YA)XB mod q . These two calculations produce identical results:

K  =  (YB)XA mod q

=  (aXB mod q)XA mod q

=  (aXB)XA mod q                                   by the rules of modular arithmetic

=  aXBXA mod q

=  (aXA)XB mod q

=  (aXA mod q)XB mod q

=  (YA)XB mod q

The result is that the two sides have exchanged a secret value. Furthermore, because XA and XB are private, an adversary only has the following ingredients to work with: q, a, YA, and YB. Thus, the adversary is forced to take a discrete logarithm to determine the key. For example, to determine the private key of user B, an adver- sary must compute

XB  = d loga,q(YB)

The adversary can then calculate the key K in the same manner as user B calculates it.

The security of the Diffie-Hellman key exchange lies in the fact that, while it is relatively easy to calculate exponentials modulo a prime, it is very difficult to calcu- late discrete logarithms. For large primes, the latter task is considered infeasible.

Here is an example. Key exchange is based on the use of the prime number       q = 353 and a primitive root of 353, in this case a  =  3. A and B select secret keys  XA  = 97 and XB  = 233, respectively. Each computes its public  key:

A computes YA  = 397 mod 353  = 40. B computes YB = 3233 mod 353 = 248.

After they exchange public keys, each can compute the common secret key:

A computes K  =  (YB)XA mod 353  =  24897 mod 353  =  160.

B computes K  =  (YA)XB mod 353  =  40233 mod 353  =  160.

We assume an attacker would have available the following information:

q = 353; a = 3; YA = 40; YB =  248

In this simple example, it would be possible by brute force to determine the secret key 160. In particular, an attacker E can determine the common key by discovering   a solution to the equation 3a mod 353 = 40 or the equation 3b mod 353 = 248. The brute-force approach is to calculate powers of 3 modulo 353, stopping when the result equals either 40 or 248. The desired answer is reached with the exponent value of 97, which provides 397 mod 353 = 40.

With larger numbers, the problem becomes impractical.

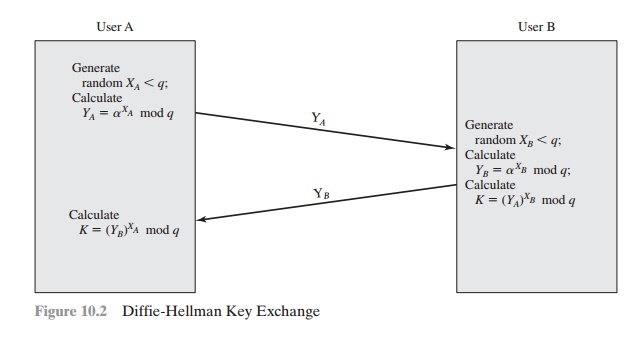
Key Exchange Protocols

Figure 10.2 shows a simple protocol that makes use of the Diffie-Hellman calcula- tion. Suppose that user A wishes to set up a connection with user B and use a secret key to encrypt messages on that connection. User A can generate a one-time private key XA, calculate YA, and send that to user B. User B responds by generating a pri- vate value XB, calculating YB, and sending YB to user A. Both users can now calcu- late the key. The necessary public values q and a would need to be known ahead of time. Alternatively, user A could pick values for q and a and include those in the first message.

As an example of another use of the Diffie-Hellman algorithm, suppose that a group of users (e.g., all users on a LAN) each generate a long-lasting private value Xi (for user i) and calculate a public value Yi. These public values, together with global public values for q and a, are stored in some central directory. At any time, user j can access user i’s public value, calculate a secret key, and use that to send an encrypted message to user A. If the central directory is trusted, then this form of communication provides both confidentiality and a degree of authentication. Because only i and j can determine the key, no other user can read the message (confidentiality). Recipient i knows that only user j could have created a message using this key (authentication). However, the technique does not protect against replay attacks.

Man-in-the-Middle Attack

The protocol depicted in Figure 10.2 is insecure against a man-in-the-middle attack. Suppose Alice and Bob wish to exchange keys, and Darth is the adversary. The attack proceeds as follows.

1.                                       Darth prepares for the attack by generating two random private keys XD1 and

XD2 and then computing the corresponding public keys YD1 and YD2.

2.                                       Alice transmits YA to Bob.

3.                                       Darth  intercepts  YA and  transmits YD1 to  Bob.  Darth  also   calculates K2  =  (YA)XD2 mod q .

4.                                       Bob receives YD1 and calculates K1  =  (YD1)XB mod q .

5.                                       Bob transmits YB to Alice.

6.                                       Darth   intercepts  Y_B and   transmits Y_D2 to   Alice.   Darth   calculates K1  =  (Y_B)^XD1 mod q

7.                                       Alice receives YD2 and calculates K2  =  (YD2)XA mod q .

At this point, Bob and Alice think that they share a secret key, but instead Bob and Darth share secret key K1 and Alice and Darth share secret key K2. All future communication between Bob and Alice is compromised in the following way.

1.                                       Alice sends an encrypted message M: E(K2, M) .

2.                                       Darth intercepts the encrypted message and decrypts it to recover M.

3.                                       Darth sends Bob E(K1, M) or E(K1, M¿) , where M¿  is any message. In the first case, Darth simply wants to eavesdrop on the communication without altering it. In  the second case, Darth wants to  modify the message going     to Bob.

The key exchange protocol is vulnerable to such an attack because it does not authenticate the participants. This vulnerability can be overcome with the use of digital signatures and public-key certificates; these topics are explored in Chapters 13 and 14.