Properties of Regression Coefficients

PROPERTIES OF REGRESSION COEFFICIENTS

1. Correlation coefficient is the geometric mean between the regression coefficients.

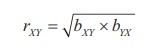
2. It is clear from the property 1, both regression coefficients must have the same sign. i.e., either they will positive or negative.

3. If one of the regression coefficients is greater than unity, the other must be less than unity.

4. The correlation coefficient will have the same sign as that of the regression coefficients.

5. Arithmetic mean of the regression coefficients is greater than the correlation coefficient.

6. Regression coefficients are independent of the change of origin but not of scale.

Properties of regression equation

1. If r = 0, the variables are uncorrelated, the lines of regression become perpendicular to each other.

2. If r = 1, the two lines of regression either coincide or parallel to each other.

3. Angle between the two regression lines is θ = tan^-1 (m₁- m₂  / 1+m₁m₂) where m1 and m2 are the slopes of regression lines X on Y and Y on X respectively. 

4. The angle between the regression lines indicates the degree of dependence between the variable.

5. Regression equations intersect at (,)

Example 5.3

Calculate the two regression equations of X on Y and Y on X from the data given below, taking deviations from actual means of X and Y.

Estimate the likely demand when the X = 25.

Solution:

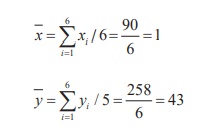
The regression line of U on V is computed as under

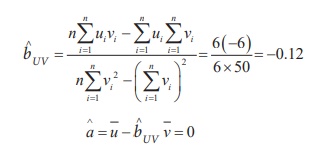
Hence, the regression line of U on V is U = ˆb_UV v + ˆa = −0.12v

Thus, the regression line of X on Y is (Y–43) = –0.25(x–15)

When x = 25, y – 43 = –0.25 (25–15)

y = 40.5

Important Note: If , are not integers then the above method is tedious and time consuming to calculate b_YX and b_XY. The following modified formulae are easy for calculation.

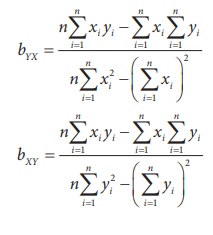
Example 5.4

The following data gives the experience of machine operators and their performance ratings as given by the number of good parts turned out per 50 pieces.

Obtain the regression equations and estimate the ratings corresponding to the experience x=15.

Solution:

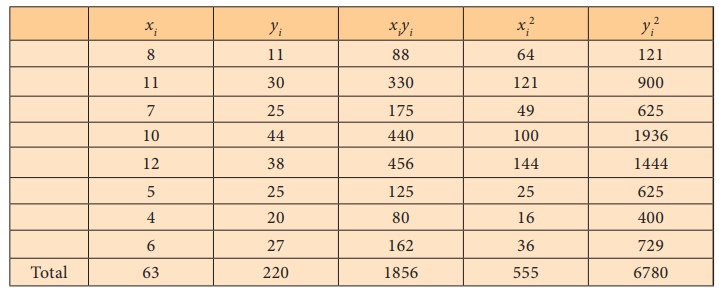
Regression equation of Y on X,

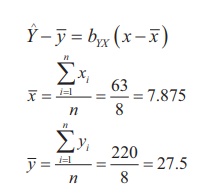
The above two means are in decimal places so for the simplicity we use this formula to compute b_YX .

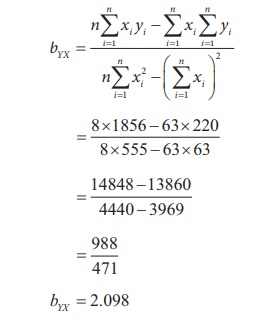
The regression equation of Y on X,

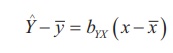
ˆY – 27.5 = 2.098 (x – 7.875)

ˆY – 27.5 = 2.098 x – 16.52

ˆY = 2.098x + 10.98

When x = 15

ˆY = 2.098 × 15 +10.98

Y = 31.47 + 10.98

= 42.45

Regression equation of X on Y,

The regression equation of X on Y,

ˆX – 7.875 = 0.169 (y – 27.5)

ˆX – 7.875 = 0.169y – 0.169 × 27.5

ˆX = 0.169y + 3.222

Example 5.5

The random sample of 5 school students is selected and their marks in statistics and accountancy are found to be

Find the two regression lines.

Solution:

The two regression lines are:

Regression equation of Y on X,

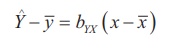
Regression equation of X on Y,

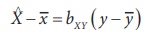
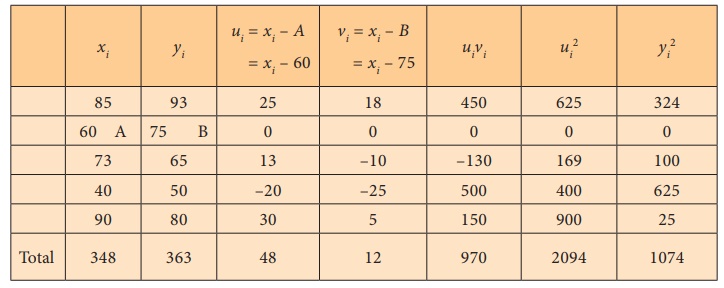
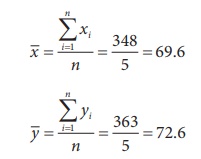
Since the mean values are in decimals format not as integers and numbers are big, we take origins for x and y and then solve the problem.

Regression equation of Y on X,

b_UV = 1.038

ˆX – 69.6 = 1.038 (y – 72.6)

ˆX – 69.6 = 1.038y – 75.359

ˆX = 1.038y – 5.759

Example 5.6

Is there any mistake in the data provided about the two regression lines Y = −1.5 X + 7, and X = 0.6 Y + 9? Give reasons.

Solution:

The regression coefficient of Y on X is b_YX = –1.5

The regression coefficient of X on Y is b_XY = 0.6

Both the regression coefficients are of different sign, which is a contrary. So the given equations cannot be regression lines.

Example: 5.7

Correlation coefficient: 0.5

Estimate the yield when rainfall is 9 inches

Solution:

Let us denote the dependent variable yield by Y and the independent variable rainfall by X.

Regression equation of Y on X is given by

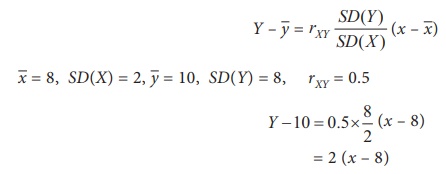
When x = 9,

Y – 10 = 2 (9 – 8)

Y = 2 + 10

= 12 kg (per unit area)

Corresponding to the annual rain fall 9 inches the expected yield is 12 kg ( per unit area).

Example 5.8

For 50 students of a class the regression equation of marks in Statistics ( X) on marks in Accountancy (Y) is 3Y – 5X + 180 = 0. The mean marks in of Accountancy is 50 and variance of marks in statistics is 16/25 of the variance of marks in Accountancy.

Find the mean marks in statistics and the coefficient of correlation between marks in the two subjects when the variance of Y is 25.

Solution:

We are given that:

n = 50, Regression equation of X on Y as 3Y – 5X + 180 = 0

 = 50 , V (X) = 16/25 V (Y ) , and V(Y) = 25.

We have to find (i)  and (ii) r_XY

(i) Calculation for 

Since (,) is the point of intersection of the two regression lines, they lie on the regression line 3Y – 5X + 180 = 0

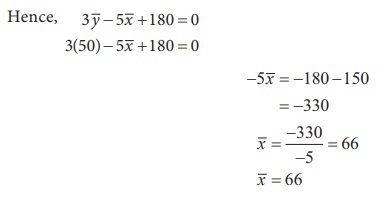
(ii) Calculation for coefficient of correlation.

3Y - 5 X + 180 = 0

- 5 X = - 180 - 3Y

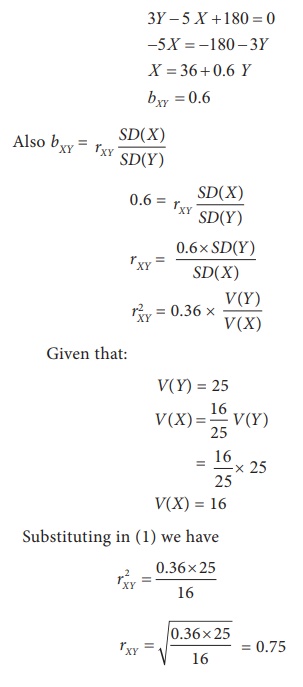
Example 5.9

If two regression coefficients are b_YX = 5/6 and b_XY = 9/20 , what would be the value of r_XY?

Solution:

The correlation coefficient r_{XY  =}

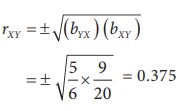
Since both the signs in b_YX and b_XY are positive, correlation coefficient between X and Y is positive.

Example 5.10

Given that b_YX = 18/7 and b_XY = -5/6 . Find r ? 

Solution:

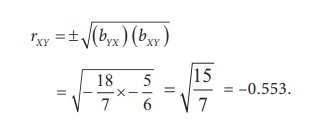
Since both the signs in b_YX and b_XY are negative, correlation coefficient between X and Y is negative.