Definition and Types of Regression

DEFINITION

Regression analysis is a statistical method of determining the mathematical functional relationship connecting independent variable(s) and a dependent variable.

Types of ‘Regression’

Based on the kind of relationship between the dependent variable and the set of independent variable(s), there arises two broad categories of regression viz., linear regression and non-linear regression.

If the relationship is linear and there is only one independent variable, then the regression is called as simple linear regression. On the other hand, if the relationship is linear and the number of independent variables is two or more, then the regression is called as multiple linear regression. If the relationship between the dependent variable and the independent variable(s) is not linear, then the regression is called as non-linear regression.

1. Simple Linear Regression

It is one of the most widely known modeling techniques. In this technique, the dependent variable is continuous, independent variable(s) can be continuous or discrete and nature of relationship is linear. This relationship can be expressed using a straight line equation (linear regression) that best approximates all the individual data points.

Simple linear regression establishes a relationship between a dependent variable ( Y) and one independent variable (X) using a best fitted straight line (also known as regression line).

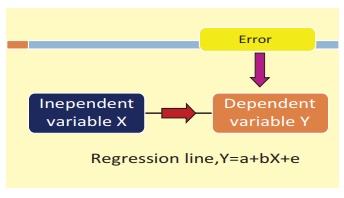
The general form of the simple linear regression equation is Y = a + bX + e, where ‘X’ is independent variable, ‘Y’ is dependent variable, a’ is intercept, ‘b’ is slope of the line and ‘ e’ is error term. This equation can be used to estimate the value of response variable (Y) based on the given values of the predictor variable (X) within its domain.

2. Multiple Linear Regression

In the case of several independent variables, regression analysis also allows us to compare the effects of independent variables measured on different scales, such as the effect of price changes and the number of promotional activities.

Multiple linear regression uses two or more independent variables to estimate the value(s) of the response variable (Y).

The general form of the multiple linear regression equation is Y = a + b₁X₁ ⁺ b₂X₂ + b₃X₃ + ... + b_tX_t + e

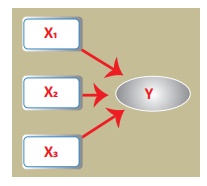
Here, Y represents the dependent (response) variable, X_i represents the i^th independent variable (regressor), a and b_i are the regression coefficients and e is the error term.

Suppose that price of a product (Y) depends mainly upon three promotional activities such as discount (X₁), instalment scheme (X₂) and free installation (X₃). If the price of the product has linear relationship with each promotional activity, then the relationship among Y and X₁, X₂ and X₃ may be expressed using the above general form as

Y = a + b₁ X ₁ + b₂ X ₂ + b₃ X ₃ + e .

These benefits help market researchers / data analysts / data scientists to eliminate and evaluate the best set of variables to be used for building regression models for predictive purposes.

3. Non-Linear Regression

If the regression is not linear and is in some other form, then the regression is said to be non-linear regression. Some of the non-linear relationships are displayed below.