Example Solved Problems | Regression Analysis - Method of Least Squares | 12th Statistics : Chapter 5 : Regression Analysis
Chapter: 12th Statistics : Chapter 5 : Regression Analysis
Method of Least Squares
METHOD OF LEAST SQUARES
In most of the cases, the data points do not fall on a straight
line (not highly correlated), thus leading to a possibility of depicting the
relationship between the two variables using several different lines. Selection
of each line may lead to a situation where the line will be closer to some
points and farther from other points. We cannot decide which line can provide
best fit to the data.
Method of least squares can be used to determine the line of best
fit in such cases. It determines the line of best fit for given observed data
by minimizing the sum of the squares of the vertical deviations from each data
point to the line.
1. Method of Least Squares
To obtain the estimates of the coefficients ‘a’ and ‘b’,
the least squares method minimizes the sum of squares of residuals. The
residual for the ith data point ei is
defined as the difference between the observed value of the response variable, yi,
and the estimate of the response variable, ŷi, and is
identified as the error associated with the data. i.e., ei
= yi–ŷi , i =1 ,2, ..., n.
The method of least squares helps us to find the values of
unknowns ‘a’ and ‘b’ in such a way that the following two
conditions are satisfied:
Sum of the residuals is zero. That is 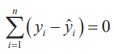
Sum of the squares of the residuals E ( a , b )
= 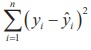 is the least
is the least
2. Fitting of Simple Linear Regression Equation
The method of least squares can be applied to determine the
estimates of ‘a’ and ‘b’ in the simple linear regression
equation using the given data (x1,y1), (x2,y2),
..., (xn,yn) by minimizing

Here, yˆi = a + bx i
is the expected (estimated) value of the response variable for given xi.
It is obvious that if the expected value (y^ i)
is close to the observed value (yi), the residual will be
small. Since the magnitude of the residual is determined by the values of ‘a’
and ‘b’, estimates of these coefficients are obtained by minimizing the
sum of the squared residuals, E(a,b).
Differentiation of E(a,b) with respect to ‘a’ and ‘b’
and equating them to zero constitute a set of two equations as described below:
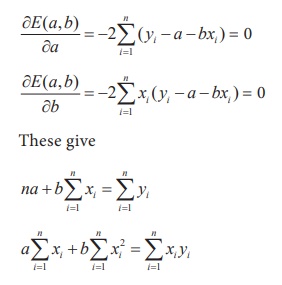
These equations are popularly known as normal equations.
Solving these equations for ‘a’ and ‘b’ yield the
estimates ˆa and ˆb.
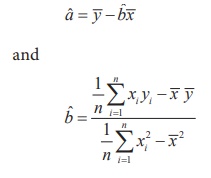
It may be seen that in the estimate of ‘ b’, the numerator
and denominator are respectively the sample covariance between X and Y,
and the sample variance of X. Hence, the estimate of ‘b’ may be
expressed as

Further, it may be noted that for notational convenience the
denominator of bˆ above is mentioned as variance of nX.
But, the definition of sample variance remains valid as defined in Chapter I,
that is,
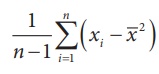
From Chapter 4, the above estimate can be expressed using, rXY
, Pearson’s coefficient of
the simple correlation between X and Y,
as
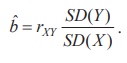
Important Considerations in the Use of Regression Equation:
1. Regression equation exhibits only the
relationship between the respective two variables. Cause and effect study shall
not be carried out using regression analysis.
2. The regression equation is fitted to the given values of the
independent variable. Hence, the fitted equation can be used for prediction
purpose corresponding to the values of the regressor within its range.
Interpolation of values of the response variable may be done corresponding to
the values of the regressor from its range only. The results obtained from
extrapolation work could not be interpreted.
Example 5.1
Construct the simple linear regression equation of Y on X
if
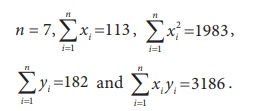
Solution:
The simple linear regression equation of Y on X to
be fitted for given data is of the form
ˆY = a + bx ……..(1)
The values of ‘a’ and ‘b’ have to be estimated from
the sample data solving the following normal equations.

Substituting the given sample information in (2) and (3), the
above equations can be expressed as
7 a + 113 b = 182 (4)
113 a + 1983 b = 3186 (5)
(4) × 113 ⇒ 791 a + 12769 b = 20566
(5) × 7 ⇒ 791 a + 13881 b = 22302
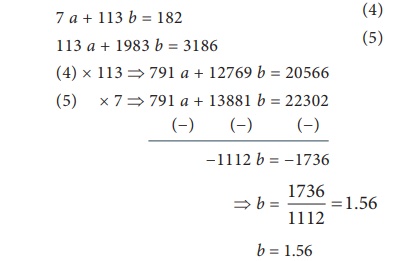
Substituting this in (4) it follows that,
7 a + 113 × 1.56 = 182
7 a + 176.28 = 182
7 a = 182 – 176.28
= 5.72
Hence, a = 0.82
Example 5.2
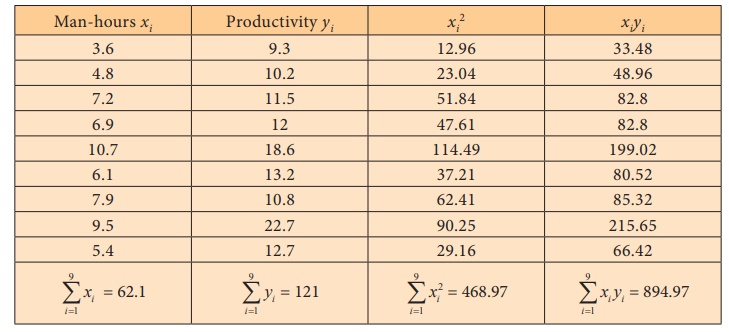
Number of man-hours and the corresponding productivity (in units)
are furnished below. Fit a simple linear regression equation ˆY = a + bx applying the
method of least squares.

Solution:
The simple linear regression equation to be fitted for the given
data is
ˆYˆ = a + bx
Here, the estimates of a and b can be calculated
using their least squares estimates
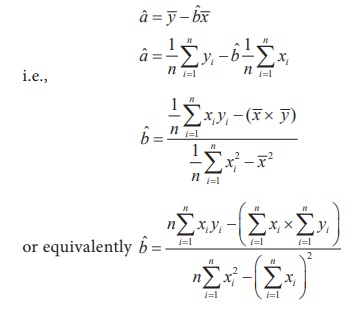
From the given data, the following calculations are made with n=9
Substituting the column totals in the respective places in the of
the estimates aˆ and bˆ , their values can be
calculated as follows:
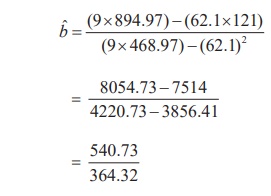
Thus, bˆ =
1.48 .
Now aˆ can be calculated using bˆ as
aˆ = 121/9 – (1.48× 62.1/9)
= 13.40 – 10.21
Hence, aˆ = 3.19
Therefore, the required simple linear regression equation fitted
to the given data is
ˆYˆ = 3.19 +1.48x
It should be noted that the value of Y can be estimated
using the above fitted equation for the values of x in its range i.e.,
3.6 to 10.7.
In the estimated simple linear regression equation of Y on X
ˆYˆ = aˆ + ˆbx
we can substitute the estimate aˆ = ![]() − bˆ
− bˆ![]() . Then, the regression equation will become as
. Then, the regression equation will become as
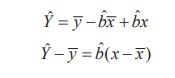
It shows that the simple linear regression equation of Y on
X has the slope bˆ and the corresponding straight line
passes through the point of averages ( ![]() ,
, ![]() ).
The above representation of straight line is popularly known in the field of
Coordinate Geometry as ‘Slope-Point form’. The above form can be applied in
fitting the regression equation for given regression coefficient bˆ
and the averages
).
The above representation of straight line is popularly known in the field of
Coordinate Geometry as ‘Slope-Point form’. The above form can be applied in
fitting the regression equation for given regression coefficient bˆ
and the averages ![]() and
and ![]() .
.
As mentioned in Section 5.3, there may be two simple linear
regression equations for each X and Y. Since the regression
coefficients of these regression equations are different, it is essential to
distinguish the coefficients with different symbols. The regression coefficient
of the simple linear regression equation of Y on X may be denoted
as bYX and the regression coefficient of the simple linear
regression equation of X on Y may be denoted as bXY.
Using the same argument for fitting the regression equation of Y
on X, we have the simple linear regression equation of X on Y
with best fit as
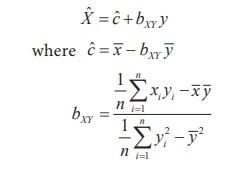
The slope-point form of this equation is
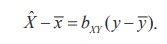
Also, the relationship between the Karl Pearson’s coefficient of
correlation and the regression coefficient are
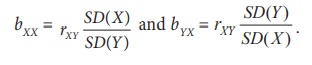
Related Topics