Probability

Probability

Few centuries ago, gambling and gaming were considered to be fashionable and became widely popular among many men. As the games became more complicated, players were interested in knowing the chances of winning or losing a game from a given situation. In 1654, Chevalier de Mere, a French nobleman with a taste of gambling, wrote a letter to one of the prominent mathematician of the time, Blaise Pascal, seeking his advice about how much dividend he would get for a gambling game played by paying money. Pascal worked this problem mathematically but thought of sharing this problem and see how his good friend and mathematician Pierre de Fermat could solve. Their subsequent correspondences on the issue represented the birth of Probability Theory as a new branch of mathematics. 

Random Experiment

A random experiment is an experiment in which 

(i) The set of all possible outcomes are known (ii) Exact outcome is not known.

Example : 1. Tossing a coin. 2. Rolling a die. 3. Selecting a card from a pack of 52 cards.

Sample space

The set of all possible outcomes in a random experiment is called a sample space. It is generally denoted by S.

Example : When we roll a die, the possible outcomes are the face numbers 1,2,3,4,5,6 of the die. Therefore the sample space is S = {1,2,3,4,5,6}

Sample point

Each element of a sample space is called a sample point.

1. Tree diagram

Tree diagram allow us to see visually all possible outcomes of an random experiment. Each branch in a tree diagram represent a possible outcome.

Illustration

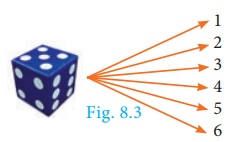
(i) When we throw a die, then from the tree diagram (Fig.8.3), the sample space can be written as S = {1,2,3,4,5,6}

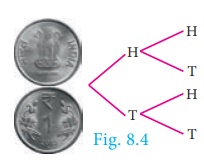
(ii) When we toss two coins, then from the tree diagram (Fig.8.4), the sample space can be written as S={HH,HT,TH,TT}

Example 8.18 Express the sample space for rolling two dice using tree diagram. 

Solution When we roll two dice, since each die contain 6 faces marked with 1,2,3,4,5,6 the tree diagram will look like

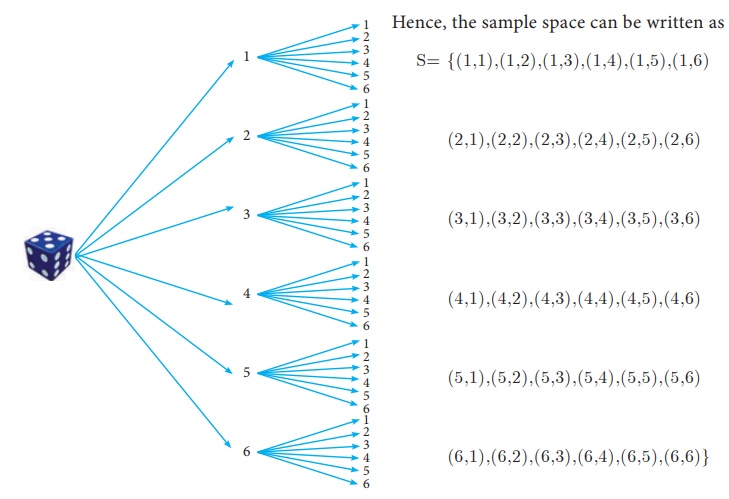
Hence, the sample space can be written as

S= {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)

(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)

(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)

(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)

(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)

(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}

Event:

 In a random experiment, each possible outcome is called an event. Thus, an event will be a subset of the sample space.

Example :

Getting two heads when we toss two coins is an event.

Trial : Performing an experiment once is called a trial.

Example : When we toss a coin thrice, then each toss of a coin is a trial.

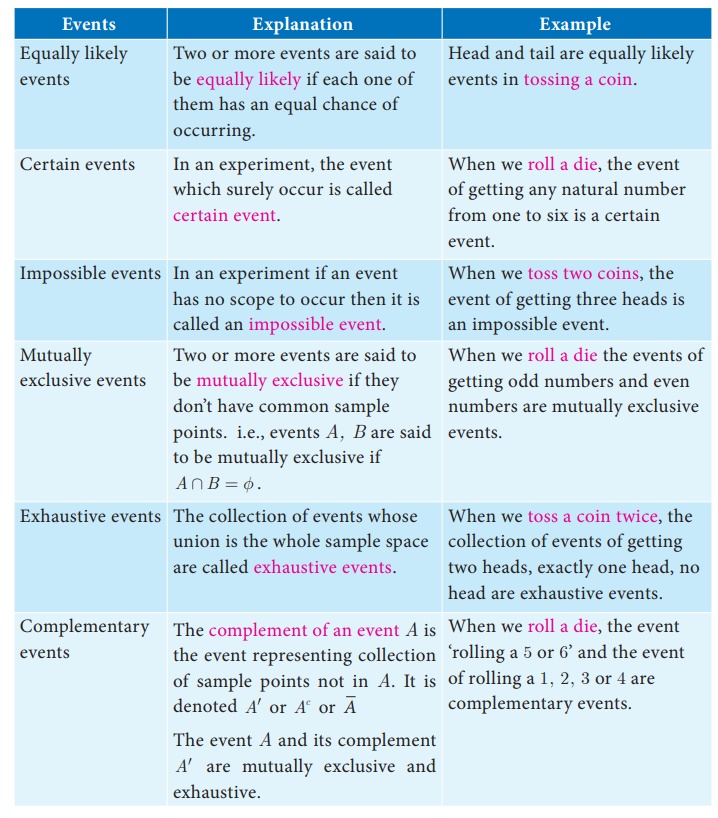
Note

Elementary event: If an event E consists of only one outcome then it is called an elementary event.

2. Probability of an Event

In a random experiment, let S be the sample space and E ⊆ S . Then if E is an event, the probability of occurrence of E is defined as

This way of defining the probability is applicable only to finite sample spaces. So in this chapter, we will be dealing problems only with finite sample spaces.

Example 8.19

A bag contains 5 blue balls and 4 green balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is (i) blue (ii) not blue.

Solution

Total number of possible outcomes n(S) = 5 + 4 = 9

(i) Let A be the event of getting a blue ball.

Number of favourable outcomes for the event A. Therefore, n(A) = 5

Probability that the ball drawn is blue. Therefore, P (A) = n(A)/ n(S) = 5/9

(ii)  will be the event of not getting a blue ball. So P () = 1 − P ( A) = 1 – 5/9 = 4/9

Example 8.20

Two dice are rolled. Find the probability that the sum of outcomes is

(i) equal to 4

(ii) greater than 10

(iii) less than 13

Solution

 When we roll two dice, the sample space is given by

S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)

(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)

(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)

(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)

(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)

(6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }; n (S) = 36

(i) Let A be the event of getting the sum of outcome values equal to 4.

Then A = {(1,3),(2,2),(3,1)}; n (A) = 3 .

Probability of getting the sum of outcomes equal to 4 is P (A) = n(A)/n(S)  = 3/36 =1/12

(ii) Let B be the event of getting the sum of outcome values greater than 10.

Then  B = {(5,6),(6,5),(6,6)}; n (B) = 3

Probability of getting the sum of outcomes greater than 10 is P (B) = n(B)/n(S)  = 3/36 =1/12

(iii) Let C be the event of getting the sum of outcomes less than 13. Here all the outcomes have the sum value less than 13. Hence C = S.

Therefore, n (C ) = n (S) = 36

Probability of getting the total value less than 13 is P (C ) = n(C)/n(S)   = 36/36 = 1.

Example 8.21

Two coins are tossed together. What is the probability of getting different faces on the coins?

Solution

When two coins are tossed together, the sample space is 

S = { HH, HT, TH, TT } ; n(S) = 4

Let A be the event of getting different faces on the coins.

A = { HT,TH } ; n(A) = 2

Probability of getting different faces on the coins is P(A) =n(A)/n(S) = 2/4 = ½

Example 8.22

 From a well shuffled pack of 52 cards, one card is drawn at random. Find the probability of getting

(i) red card

(ii) heart card

(iii) red king

(iv) face card

(v) number card

Solution

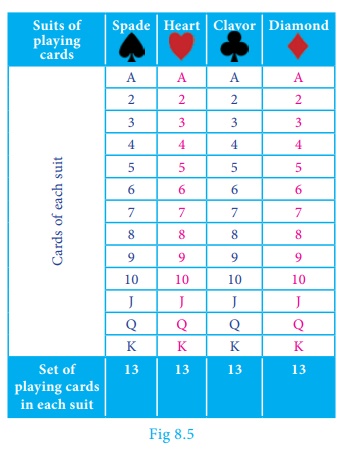
n (S) = 52

(i) Let A be the event of getting a red card.

n (A)  = 26

Probability of getting a red card is

P (A)  = 26/52 = 1/2

(ii) Let B be the event of getting a heart card.

n (B)  = 13

Probability of getting a heart card is P

 P(B) = n(B)/n(S) = 13/52 = 1/4

(iii) Let C be the event of getting a red king card. A red king card can be either a diamond king or a heart king.

n (C )  = 2

Probability of getting a red king card is

P(C) = n(C)/n(S) = 12/52 = 1/26

(iv) Let D be the event of getting a face card. The face cards are Jack (J), Queen (Q), and King (K).

n(D)  = 4 ×3 = 12

Probability of getting a face card is

P (D)  = n(D)/n(S)  = 12/52 = 3/13

(v) Let E be the event of getting a number card. The number cards are 2, 3, 4, 5, 6, 7, 8, 9 and 10.

n (E)  = 4 ×9 = 36

Probability of getting a number card is

P (E)  = n(E)/n(S)  = 36/52 = 9/13

Example 8.23

What is the probability that a leap year selected at random will contain 53 saturdays. (Hint: 366 = 52 ×7 + 2 )

Solution

 A leap year has 366 days. So it has 52 full weeks and 2 days. 52 Saturdays must be in 52 full weeks.

The possible chances for the remaining two days will be the sample space.

S = {(Sun-Mon, Mon-Tue, Tue-Wed, Wed-Thu, Thu-Fri, Fri-Sat, Sat-Sun)}

n (S) = 7

Let A be the event of getting 53^rd Saturday.

Then A = {Fri-Sat, Sat-Sun}; n (A) = 2

Probability of getting 53 Saturdays in a leap year is P ( A ) = n (A)/ n (S) = 2/7

Thinking Corner: What will be the probability that a non - leap year will have 53 Saturdays?

Example 8.24 A die is rolled and a coin is tossed simultaneously. Find the probability that the die shows an odd number and the coin shows a head.

Solution

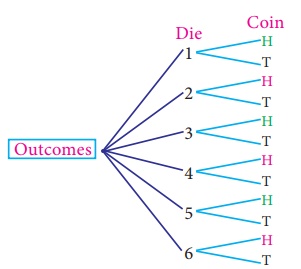
Sample space

S = {1H,1T,2H,2T,3H,3T,4H,4T,5H,5T,6H,6T};

n(S) = 12

Let A be the event of getting an odd number and a head.

A = {1H, 3H, 5H}; n(A) = 3

P (A) = n (A)/ n(S) = 3/12 = 1/4

Example 8.25

A bag contains 6 green balls, some black and red balls. Number of black  balls is as twice as the number of red balls. Probability of getting a green ball is thrice the  probability of getting a red ball. Find (i) number of black balls (ii) total number of balls.

Solution

Number of green balls is n(G) = 6

Let number of red balls is n(R) = x

Therefore, number of black balls is n(B) = 2x

Total number of balls n(S) = 6 + x + 2x = 6 + 3x

It is given that, P (G) = 3 × P(R)

6/ (6+3x) = 3 × x/(6 + 3x)

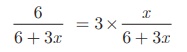
3x = 6 gives, x = 2

(i) Number of black balls = 2 × 2 = 4

(ii) Total number of balls = 6 +(3 × 2) = 12

Example 8.26

A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the numbers 1, 2, 3, …12. What is the probability that it will point to

(i) 7

(ii) a prime number

(iii) a composite number?

Solution

Sample space S = {1,2,3,4,5,6,7,8,9,10,11,12}; n(S) = 12

(i) Let A be the event of resting in 7. n(A)=1

P (A)  = n(A)/n(S) = 1/12

(ii) Let B be the event that the arrow will come to rest in a prime number.

B = {2,3,5,7,11}; n (B)  = 5

P (B)  = n(B)/n(S) = 5/12

(iii) Let C be the event that arrow will come to rest in a composite number.

C = {4,6,8,9,10,12}; n (C ) =6

P (C)  = n(C)/n(S) = 6/12 = 1/2