Problem Questions with Answer, Solution | Mathematics - Exercise 8.4: Addition Theorem of Probability | 10th Mathematics : UNIT 8 : Statistics And Probability
Chapter: 10th Mathematics : UNIT 8 : Statistics And Probability
Exercise 8.4: Addition Theorem of Probability
Exercise 8.4
1. If P (A) = 2/3 , P (B) = 2/5 , P (A ∪ B) = 1/3 then find P (A Ո B) .

2. A and B are two events such that, P (A) = 0. 42, P (B) = 0.48 , and P (A ∩ B) = 0.16 .
Find
(i) P,(not A)
(ii) P,(not B)
(iii) P,(A or B)

3. If A and B are two mutually exclusive events of a random experiment and P(not A) = 0.45, P (A U B) = 0.65, then find P (B).
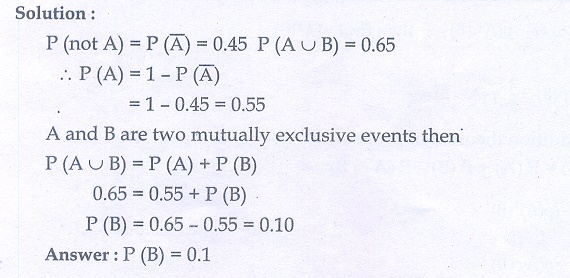
4. The probability that atleast one of A and B occur is 0.6. If A and B occur simultaneously with probability 0.2, then find P (![]() ) + P (
) + P (![]() ) .
) .

5. The probability of happening of an event A is 0.5 and that of B is 0.3. If A and B are mutually exclusive events, then find the probability that neither A nor B happen.

6. Two dice are rolled once. Find the probability of getting an even number on the first die or a total of face sum 8.

7. From a well-shuffled pack of 52 cards, a card is drawn at random. Find the probability of it being either a red king or a black queen.

8. A box contains cards numbered 3, 5, 7, 9, … 35, 37. A card is drawn at random from the box. Find the probability that the drawn card have either multiples of 7 or a prime number.

9. Three unbiased coins are tossed once. Find the probability of getting atmost 2 tails or atleast 2 heads.

10. The probability that a person will get an electrification contract is 3/5 and the probability that he will not get plumbing contract is 5/8. The probability of getting atleast one contract is 5/7. What is the probability that he will get both?

11. In a town of 8000 people, 1300 are over 50 years and 3000 are females. It is known that 30% of the females are over 50 years. What is the probability that a chosen individual from the town is either a female or over 50 years?

12. A coin is tossed thrice. Find the probability of getting exactly two heads or atleast one tail or two consecutive heads.

13. If A, B, C are any three events such that probability of B is twice as that of probability of A and probability of C is thrice as that of probability ofA and if P (A ∩ B) = 1/6. P (B ∩ C) = 1/4, P (A ∩ C) = 1/8, P (A ∪ B ∪C) = 9/10, P (A ∩ B ∩C) = 1/15, then find P (A), P (B) and P (C) ?

14. In a class of 35, students are numbered from 1 to 35. The ratio of boys to girls is 4:3. The roll numbers of students begin with boys and end with girls. Find the probability that a student selected is either a boy with prime roll number or a girl with composite roll number or an even roll number.

1. 11/15
2. (i) 0.58 (ii) 0.52 (iii) 0.74
3. 0.1
4. 1.2
5. 0.2
6. 5/9
7. 1/13
8. 13/18
9. 73/280
10. 17/40
11. 1
12. 11/48, 11/24, 11/16
Related Topics