Coefficient of Variation

Coefficient of Variation

Comparison of two data in terms of measures of central tendencies and dispersions in some cases will not be meaningful, because the variables in the data may not have same units of measurement.

For example consider the two data

Here we cannot compare the standard deviations 1. 5kg and ₹21.60. For comparing two or more data for corresponding changes the relative measure of standard deviation, called “Coefficient of variation” is used.

Coefficient of variation of a data is obtained by dividing the standard deviation by the arithmetic mean. It is usually expressed in terms of percentage. This concept is suggested by one of the most prominent Statistician Karl Pearson.

Thus, coefficient of variation of first data (C.V1) = σ₁/x₁ ×100%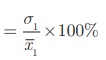 

and coefficient of variation of second data (C.V2) = σ₂/ x₂ × 100%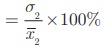 

The data with lesser coefficient of variation is more consistent or stable than the other data. Consider the two data

If we compare the mean and standard deviation of the two data, we think that the two datas are entirely different. But mean and standard deviation of B are 60% of that of A. Because of the smaller mean the smaller standard deviation led to the misinterpretation.

To compare the dispersion of two data, coefficient of variation = σ/x ×100% 

The coefficient of variation of A = 191. 5/700 ×100% = 27. 4%

The coefficient of variation of B = 114. 9/420 ×100% = 27. 4%

Thus the two data have equal coefficient of variation. Since the data have equal coefficient of variation values, we can conclude that one data depends on the other. But the data values of B are exactly 60% of the corresponding data values of A. So they are very much related. Thus, we get a confusing situation.

To get clear picture of the given data, we can find their coefficient of variation. This is why we need coefficient of variation.

Example 8.15

The mean of a data is 25.6 and its coefficient of variation is 18.75. Find the standard deviation.

Solution

Mean  = 25. 6 , Coefficient of variation, C.V. = 18.75

Coefficient of variation, C.V. = σ/ ×100%

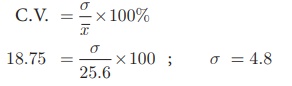
Example 8.16

The following table gives the values of mean and variance of heights and weights of the 10th standard students of a school.

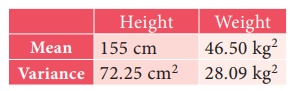
Which is more varying than the other? 

Solution

For comparing two data, first we have to find their coefficient of variations

Mean 1= 155cm, variance σ₁² = 72. 25 cm²

Therefore standard deviation σ₁ = 8. 5

Coefficient of variation 

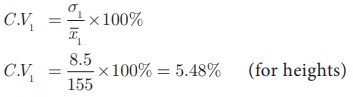
Mean 2 = 46.50 kg, Variance σ₂² = 28.09 kg2

Standard deviation σ₂ = 5. 3kg 

Coefficient of variation 

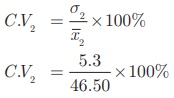
= 11. 40% (for weights)

C .V₁ = 5.48% and C .V₂  = 11.40%

Since C .V₂  > C .V₁ , the weight of the students is more varying than the height.

Example 8.17 

The consumption of number of guava and orange on a particular week by a family are given below.

Which fruit is consistently consumed by the family?

Solution

First we find the coefficient of variation for guavas and oranges separately.

C .V₁ = 23.54% , C .V₂ = 65.50% Since, C .V₁<C .V₂ ,  we  can conclude  that  the consumption of guavas is more consistent than oranges.