Principles of Counting

Principles of Counting

There are some basic counting techniques which will be useful in determining the number through different ways of arranging or selecting objects. The basic counting principles are given below.

1. Addition principle

If there are two selections such that they can be done independently in m ways and n ways respectively, then either of the two selections can be done in (m + n) ways.

Let us learn about this addition principle of counting as given below :

Situation:

In class VIII, there are 16 boys and 9 girls. The teacher wants to select either a boy or a girl as the class leader. Let us see, in how many ways can the teacher select the class leader.

The teacher can select the class leader in any one of the following ways.

(i) In the first choice, the teacher can select a boy among 16 boys in 16 ways (who ever may be of the 16 boys).

(ii) In the second choice, the teacher can select a girl among 9 girls in 9 ways (who ever may be of the 9 girls).

Hence, the teacher can select the class leader who is a boy or a girl in 25 different ways (16 boys + 9 girls).

Thus, we come to know, if a selection A can occur in m ways and another selection B can occur in n ways, and suppose that both cannot occur together, then A or B can occur in (m + n) ways. Let us see an example.

Example 7.1

If you are going to a hotel to have food and the hotel offers different food items as shown in Fig 7.2. Find how many ways are possible to have either tiffin or meals?

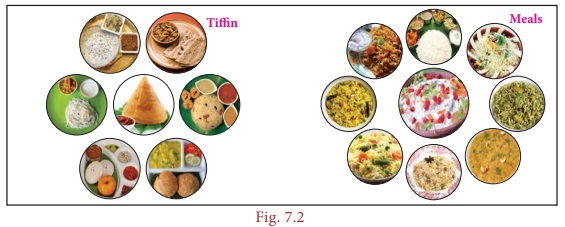
Solution:

From the above Fig. 7.2, we come to know

(i) For tiffin, we can choose one among 7 items in 7 ways

(ii) For meals, we can choose one among 9 items in 9 ways.

Therefore, there are 16 (7 tiffin items + 9 meals items) different ways by which we can choose any one food.

2. Multiplication principle

If a selection can be performed in m ways, following which another selection can be performed in n ways, and both the selections are dependent on each other then, the two selections together can be performed in exactly (m × n) different ways.

Now, we shall learn about multiplication principle of counting from the following situation.

Situation:

There are 3 places in a city namely A,B and C. There are 3 routes a1, a2 and a3 from A to B. There are 2 different routes, b1 and b2 from B to C as shown in the Fig 7.3.

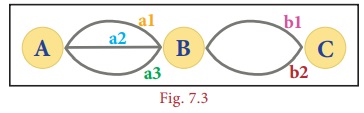
Suppose a person wants to travel from A to C via B. Lets us see the number of ways he can go from place A to C via B.

(i) In the first way, he can go from A to B in 3 routes and

(ii) In the second way, he can go from B to C in 2 different routes.

Therefore, the total number of ways in which he can travel is 6 (3 × 2) routes as shown in Fig 7.4.

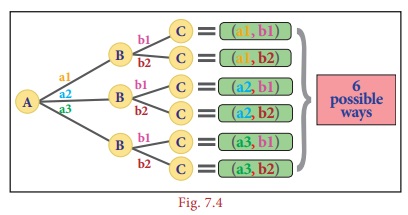
Thus, we come to know, if a selection A can occur in m ways and another selection B can occur in n ways, and both the selections are dependent on each other then, the two selections can be performed in exactly (m × n) different ways. Let as learn more about from the following examples.

Example 7.2

Praveen bought 3 shirts, 2 jeans and 3 pairs of shoes for his birthday. In Fig. 7.5 shows the different ways of wearing the dress. In how many different ways can Praveen wear a dress on his birthday?

Solution:

Here, Praveen has 3 shirts  , 2 jeans  and  3 pairs of shoes.

He can wear a dress either this way  or he can have the choices as shown in the Fig. 7.6

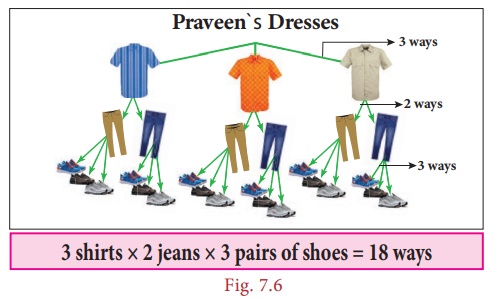
Therefore, Praveen can wear his dress in 18 (3×2×3) different possible ways on his birthday.

Example 7.3

In class VIII, a math club has four members M,A,T and H. Find the number of different ways, the club can elect

(i) a leader,

(ii) a leader and an assistant leader.

Solution:

(i) To elect a leader

In class VIII, a math club has four members namely M, A, T and H.

Therefore, there are 4 (4 × 1) different ways by which they can be elected a leader.

(ii) To elect a leader and an assistant leader

In the Fig. 7.7, the red shaded boxes show that same member comes twice. As, one person cannot have two leadership, therefore, the red shaded boxes cannot be counted. So there are only 12 ((4 × 1 × 4) – 4) different ways (shown in yellow boxes and green boxes) to choose a leader and an assistant leader for the math club.

Activity

1. Determine the number of two digit numbers that can be formed using the digits 1, 3 and 5 with repetition of digits allowed.

The activity consists of two parts

(i) Choose a one's digit.

(ii) Choose a ten's digit.

Complete the table given beside

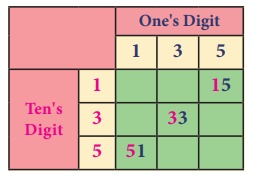
Solution:

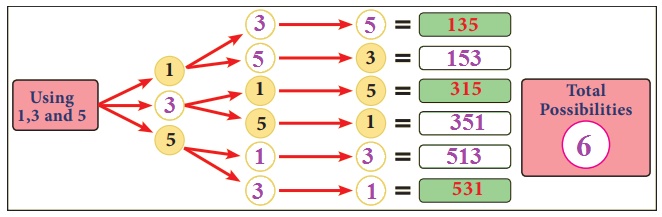
2. Find the three digit numbers that can be formed using the digits 1, 3 and 5 without repetition of digits.

Complete the tree diagram given below to the numbers

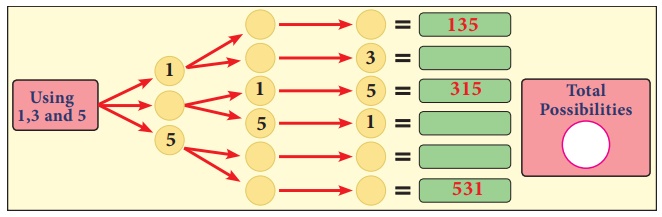
Solution:

A password using 6 characters is created where the first 2 characters are any of the alphabets, the third character is any one special character like @, #, $, %, &, _,+,~, * or - and the last 3 characters are any of the numbers from 0 to 9. For that, there are 26 × 26 × 10 × 10 × 10 × 10 = 67,60,000 number of different ways possible to create that password.

Example 7.4

In how many ways, can the students answer 3 true or false type questions in a slip test?

Solution:

(i) Assuming that the question Q₁ is answered True, questions Q₂ and Q₃ can be answered as TT, TF, FT and FF in 4 ways.

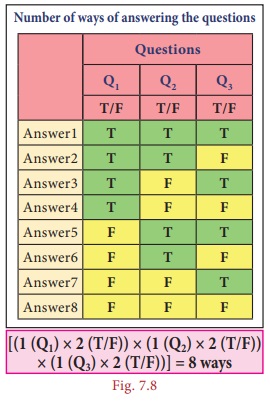
(ii) Assuming that the question Q₁ is answered False, Q₂ and Q₃ can also be answered as TT, TF, FT, and FF in 4 ways.

Thus, as each question has only two options (True or False) in 2 ways, the number of ways of answering these 3 questions in a slip test is 8 (2 x 2 x 2) possible ways as shown in Fig. 7.8.

Example 7.5

Madhan wants to a buy a new car. The following choices are available for him.

• There are 2 types of cars as shown in the Fig. 7.9

• There are 5 colours available in each type as shown in Fig. 7.9.

• There are 3 models available in each colour

(i) GL (standard model)

(ii) SS (sports model)

(iii) SL (luxury model)

(i) In how many different ways can Madhan buy any one of the new car?

(ii) If the white colour is not available in Type 2, then in how many ways can Madan buy a new car among the given option?

Solution:

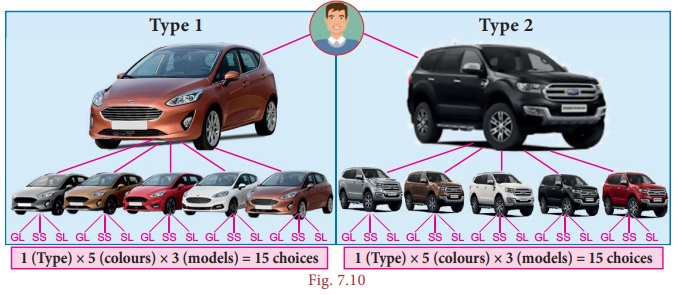
(i) To buy any one of the new car from the given choices

Here, we have 2 types of car with 5 different colours and 3 models in each colour.

Therefore, there are 30 [2 (1 × 5 × 3)] different ways to buy a new car by Madhan.

(ii) If the white colour is not available in Type 2, then...

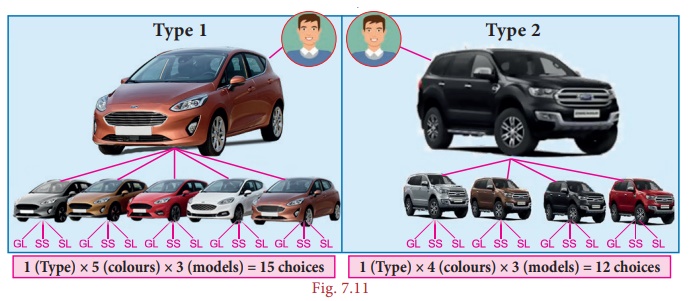
(i) For Type 1, we have 5 colours and 3 models and hence there are 1 × 5 × 3 = 15 choices.

(ii) For Type 2, we have only 4 colours and 3 models and hence there are 1 × 4 × 3 = 12 choices. Therefore, there are 27 (15 + 12) different ways to buy a new car by Madhan

The above example illustrates both the addition and multiplication principles.