Exercise 7.2

Exercise 7.2

1. Using repeated division method, find the HCF of the following:

(i) 455 and 26

(ii) 392 and 256

(iii) 6765 and 610

(iv) 184, 230 and 276

(i) 455 and 26

Solution:

Step 1: The larger number should be dividend = 455

& smaller number should be divisor = 26

Step 2: After 1st division, the remainder becomes new divisor & the previous divisor becomes next dividend.

Step 3: This is done till remainder is zero.

Step 4: The last divisor is the HCF

∴ Answer: The HCF is 13.

(ii) 392 and 256

Solution:

256 is smaller, so it is the 1st divisor

 8 is the last divisor & hence the HCF.

∴  HCF = 8

(iii) 6765 and 610

Solution:

5 is the last divisor &  hence the HCF

∴  HCF = 5

(iv) 184, 230 and 276

Solution:

First let us take 184 & 230

46 - Last divisor is the HCF

46 is the HCF of 184, and 230.

Now the HCF of the first two numbers is the dividend for the third number.

∴  Answer: HCF of 184, 230 & 276 is 46

2. Using repeated subtraction method, find the HCF of the following:

(i) 42 and 70

(ii) 36 and 80

(iii) 280 and 420

(iv) 1014 and 654

(i) 42 and 70

Solution: 

Let number be m & n  m > n

We do m − n & the result of subtraction becomes new 'm'. if m becomes less than n, we do n − m and then assign the result as n. We should do this till m = n. When m = n then 'm’ is the HCF.

42 and 70                m = 70,                  n = 42

70 – 42 = 28,         now m = 42,          n = 28

42 − 28 = 14,         now m =  28,         n = 14

28 – 14 = 14,         now m = 14,         n = 14 ; we stop here as m = n

∴  HCF of 42 & 70 is 14

(ii) 36 and 80

Solution:

36 and 80               m = 80,               n = 36

80 − 36 = 44,         now n = 44,         m = 36

Since n > m, we should do n − m

44 − 36 = 8,         now n = 8,         m = 36

36 − 8 = 28          Similarly, processing, proceeding, we do repeated subtraction till m = n

28 − 8 = 20

20 – 8 = 12

12 − 8 = 4

8 − 4 = 4          now m = n = 4           ∴ HCF is 4

(iii) 280 and 420

Solution:

Let m = 420, n = 280

m − n = 420 – 280 = 140

now m = 280, n = 140

m − n = 280 – 140 = 140

now m = n = 140

∴  HCF is 140

(iv) 1014 and 654

Solution:

Let m = 1014, n = 654

m − n = 1014 − 654 = 360

now m = 654, n = 360

m − n = 654 − 360 = 294

now m = 360, n = 294

m − n = 360 − 294 = 66

now m = 294, n = 66

m − n = 294 − 66 = 228

now m = 66, n = 228

n − m = 228 – 66 = 162

now m = 162, n = 66

∴  m − n = 162 − 66 = 96

n − m = 96 − 66 = 30

Similarly, 66−30 = 36

36 − 30 = 6

30 − 6 = 24

24 − 6 = 18

18 − 6 = 12

12 − 6 = 6 now m = n

∴  HCF of 1014 and 654 is 6

3. Do the given problems by repeated subtraction method and verify the result.

(i) 56 and 12

(ii) 320, 120 and 95

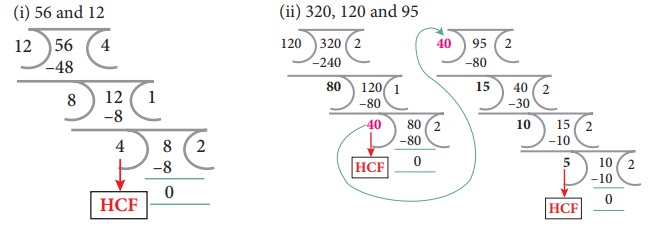
(i) 56 and 12

Solution:

56 & 12

Let n = 56 & n = 12

m − n = 56 − 12 = 44

now m = 44, n = 12

m − n = 44 − 12 = 32

m − n = 32 − 12 = 20

m − n = 20 − 12 = 8

n − m = 12 − 8 = 4

m − n = 8 − 4 = 4. now m = n

∴ HCF of 56 & 12 is 4

(ii) 320, 120 and 95

Solution:

Let us take 320 & 120 first m = 320, n = 120

m − n = 320 − 120 = 200

m = 200, n = 120

∴ m − n = 200 − 120 = 80

120 − 80 = 40

80 − 40 = 40

∴ m = n = 40 → HCF of 320, 120

Now let us find HCF of 40 & 95

m = 95, n = 40

∴ m − n = 95 − 40 = 55

55 − 40 = 15

40 − 15 = 25

25 − 15 = 10

15 − 10 = 5 HCF of 40 & 95 is 5

10 − 5 = 5

∴ HCF of 320, 120 & 95 is 5

4. Kalai wants to cut identical squares as big as she can, from a piece of paper measuring 168mm and by 196mm. What is the length of the side of the biggest square? (To find HCF using repeated subtraction method)

Solution: 

Sides are 168 & 196

To find HCF of 168 & 196, we are to use repeated subtraction method.

∴ m = 196, n = 168

m − n = 196 − 168 = 28          now n = 28, m = 168

m − n = 168 – 28 = 140          now m = 140, n = 28

m − n = 140 – 28 = 112          now m = 112, n = 28

m − n = 112 − 28 = 84           now m = 84, n = 28

m − n = 84 − 28 = 56           now m = 56, n = 28

m − n = 56 − 28 = 28

∴ HCF is 28

∴ Length of biggest square is 28

Objective Type Questions

5. What is the eleventh Fibonacci number?

(a) 55

(b) 77

(c) 89

(d) 144

[Answer: (c) 89]

Solution:

∴ 11^th Fibonacci number is 89

6. If F(n) is a Fibonacci number and n =8, which of the following is true?

(a) F(8) = F(9)+F(10)

(b) F(8) = F(7)+F(6)

(c) F(8) = F(10)×F(9)

(d) F(8) = F(7)–F(6)

[Answer: (b) F(8) = F(7) + F(6)]

Solution:

Given F(n) is a Fibonacci number & n = 8

∴ F(8) = F(7) + F (6) as any term in Fibonacci series is the sum of preceding 2 terms

7. Every 3rd number of the Fibonacci sequence is a multiple of _______

(a) 2

(b) 3

(c) 5

(d) 8

[Answer: (a) 2]

Solution: Every 3^rd number in Fibonacci sequence is a multiple of 2

8. Every _______ number of the Fibonacci sequence is a multiple of 8

(a) 2nd

(b) 4th

(c) 6th

(d) 8th

[Answer: (c) 6^th]

9. The difference between the 18th and 17th Fibonacci number is

(a) 233

(b) 377

(c) 610

(d) 987

[Answer: (d) 987]

Solution:

F(18) = F(17) + F(16)

F(18) − F(17) = F(16) = F(15) + F(14)

= 610 + 377 = 987

10. Common prime factors of 30 and 250 are

 (a) 2 × 5

(b) 3 × 5

(c) 2 × 3 × 5

(d) 5 × 5

[Answer: (a) 2 × 5]

Solution:

Prime factors of 30 are 2 × 3 × 5

Prime factors of 250 are 5 × 5 × 5 × 2

∴  Common prime factors are 2 × 5

11. Common prime factors of 36, 60 and 72 are

 (a) 2 × 2

(b) 2 × 3

(c) 3 × 3

(d) 3 × 2 × 2

[Answer: (d) 3 × 2 × 2]

Solution:

Prime factors of 36 are 2 × 2 × 3 × 3

Prime factors of 60 are 2 × 2 × 3 × 5

Prime factors of 72 are 2 × 2 × 2 × 3 × 3

∴  Common prime factors are 2 × 2 × 3

12. Two numbers are said to be co-prime numbers if their HCF is

(a) 2

(b) 3

(c) 0

(d) 1

[Answer: (d) 1]

Answer:

Exercise 7.2

1. (i) 13 (ii) 8 (iii) 5 (iv) 46

2. (i) 14 (ii) 4 (iii) 140 (iv) 6

3. (i) 4 (ii) 5

4. 14

5. 28

6. (C) 89

7) (B) F(8) = F(7)+F(6)

8. (A) 2

9. (C) 6th

10) (D) 987

11. (A) 2×5 

12. (D)  3×2×2  not (B) 2×3

13. (D) 1