Fibonacci Numbers

Fibonacci Numbers

We have learnt in earlier classes, on how all beautiful things in nature as well as man made things are connected with Mathematics. Now, we just refresh everyone’s memory and show how Math can be beautiful when seen in physical and biological things everywhere around us.

Fibonacci (real name Leonardo Bonacci) was an Italian mathematician who developed the Fibonacci Sequence. Remember the pattern of the Fibonacci sequence we already studied in standard VI it looks like this: 1, 1, 2, 3, 5, 8, 13, 21, 34... and it goes on.

Let us tabulate the Fibonacci sequence and find a rule.

We observe that the 3^rd term of the Fibonacci sequence is the sum of 2^nd term and the 1^st term.

That is, F(3) = F(2) + F(1) and so we can extend and write the rule is

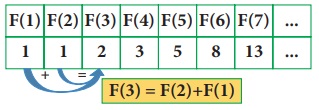
F(n)= F(n–1) + F(n–2)

where F(n) is the n^th term

F(n–1) is the previous term to the n^th term

F(n–2) is the term before the (n–1)^th term

This is how the Fibonacci Sequence is obtained. Let us learn more from the following real life examples.

Situation:

Let us look at the family tree of a male drone bee and a female bee as shown Fig 7.19.

Here, female bees have 2 parents, male (drone) bees have just one parent, a female. (Male bee (drone) are produced by the queen’s unfertilized eggs, so male(drone) bees only have a mother but no father!)

From the picture the following points are noted:

1. The male  has 1 parent, a female .

2. The male  has 2 grandparents , since his mother had parents  , a male and a female.

3. The male  has 3 great-grandparents : since his grandmother has two parents but his grandfather has only one.

Now, answer, how many great-great-grandparents did the male  have?

Let us try to find the relationship among the pattern of bees family by representing in the tabular form given below,

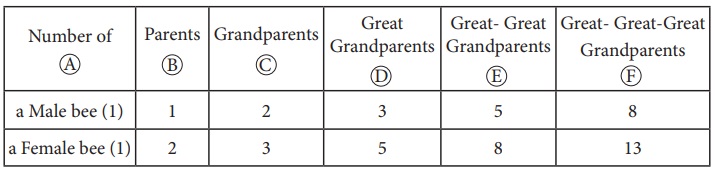
We see the Fibonacci numbers 1, 1, 2, 3, 5, 8, 13… in the above table.

Note

 The difference between two consecutive numbers of the Fibonacci sequence increase very quickly. ((For example F(5) – F(4) = 5 – 3 = 2 ; F(10) – F(9) = 55 – 34 = 21 ; F(15) – F(14) = 610 – 377 = 233)(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946 ...))

Example 7.7

Given that one pair of new born rabbits they produce a new pair each month and from the second month, each new pair can breed themselves. Find how many pairs of rabbits are bred from one pair in a year, and find the relationship between the number of months and the number of pairs of rabbits by tabulation (a pair means (a male and a female)).

Solution:

The below picture clearly forms the sequence is 1,1,2,3,5,8... Here, we find the pattern in which each number is in the Fibonacci sequence, obtained by adding together with previous two. Going on like this to find subsequent numbers at the twelfth month, we will get 144 pairs of rabbits. In the other words, twelfth Fibonacci number is 144.

Activity

Using the given Table I, find the pattern, answer the following questions and colour the values in the given Table II. One is done for you.

Table I

1. Where are the even Fibonacci Numbers? Colour both the term n and where F(n) is even in yellow. Do you find any pattern? Every Third Fibonacci number is a multiple of 2(even).

2. Where there are Fibonacci numbers which are multiple of 3 ? Colour both the term n and where F(n) is multiple of 3 in red.

Write down the pattern you find

Every 4^th Fibonacci number is a multiple of 3.

3. What about the multiple of 5? Colour both the term n and where F(n) is multiple of 5 in blue. Write down the pattern you find.

Every 5^th Fibonacci number i.e. a multiple of F(5) or 5 = F(5)

4. What about the multiple of 8? Colour both the term n where F(n) is multiple of 8 in green. Write down the pattern you find.

Every 6^th Fibonacci number i.e a multiple of F(6) or 8 = F(6)

Table II

From the above activity, we conclude that

Every Fibonacci number is a factor of (a term number of) Fibonacci numbers in miltiples.

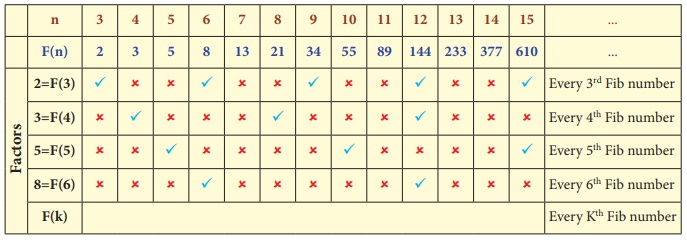
From the above table, we get a general rule as Every k^th Fibonacci number is a multiple of F(k).