Power System Response Characteristics

Power System Response Characteristics:

The power system response characteristics are:

1.  The system impedance characteristics

2.     The presence of a capacitor bank causing resonance

3.     The amount of resistive loads in the system

1. System impedance

At the fundamental frequency, power systems are primarily inductive, and the equivalent impedance is sometimes called simply the short-circuit reactance. Capacitive effects are frequently neglected on utility distribution systems and industrial power systems. One of the most frequently used quantities in the analysis of harmonics on power systems is the short-circuit impedance to the point on a network at which a capacitor is located. If not directly available, it can be computed from short-circuit study results that give either the short-circuit mega volt ampere (MVA) or the short-circuit current as follows:

ZSC is a phasor quantity, consisting of both resistance and reactance. However, if the short-circuit data contain no phase information, one is usually constrained to assuming that the impedance is purely reactive. This is a reasonably good assumption for industrial power systems for buses close to the mains and for most utility systems. When this is not the case, an effort should be made to determine a more realistic resistance value because that will affect the results once capacitors are considered. The inductive reactance portion of the impedance changes linearly with frequency. One common error made by novices in harmonic analysis is to forget to adjust the reactance for frequency. The reactance at the hth harmonic is determined from the fundamental impedance reactance X1 by:

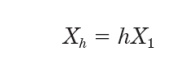
In most power systems, one can generally assume that the resistance does not change significantly when studying the effects of harmonics less than the ninth. For lines and cables, the resistance varies approximately by the square root of the frequency once skin effect becomes significant in the conductor at a higher frequency. The exception to this rule is with some transformers.

Because of stray eddy current losses, the apparent resistance of larger transformers may vary almost proportionately with the frequency. This can have a very beneficial effect on damping of resonance as will be shown later. In smaller transformers, less than 100 kVA, the resistance of the winding is often so large relative to the other impedances that it swamps out the stray eddy current effects and there is little change in the total apparent resistance until the frequency reaches about 500 Hz. Of course, these smaller transformers may have an X/R ratio of 1.0 to 2.0 at fundamental frequency, while large substation transformers might typically have a ratio of 20 to 30. Therefore, if the bus that is being studied is dominated by transformer impedance rather than line impedance, the system impedance model should be considered more carefully. Neglecting the resistance will generally give a conservatively high prediction of the harmonic distortion.

At utilization voltages, such as industrial power systems, the equivalent system reactance is often dominated by the service transformer impedance. A good approximation for XSC may be based on the impedance of the service entrance transformer only:

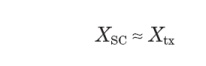
While not precise, this is generally at least 90 percent of the total impedance and is commonly more. This is usually sufficient to evaluate whether or not there will be a significant harmonic resonance problem. Transformer impedance in ohms can be determined from the percent impedance Ztx found on the nameplate by

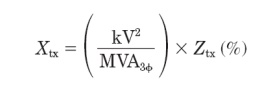
where MVA3_ is the kVA rating of the transformer. This assumes that the impedance is predominantly reactive. For example for a 1500-kVA, 6 percent transformer, the equivalent impedance on the 480-V side is

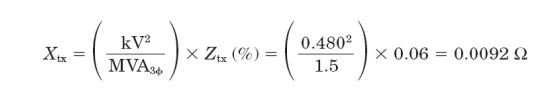
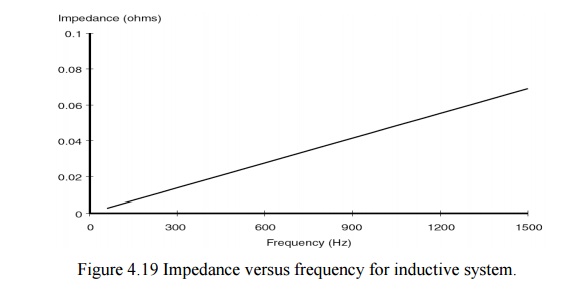
A plot of impedance versus frequency for an inductive system (no capacitors installed) would look like Fig. 4.19. Real power systems are not quite as well behaved. This simple model neglects capacitance, which cannot be done for harmonic analysis.

2. Capacitor impedance

Shunt capacitors, either at the customer location for power factor correction or on the distribution system for voltage control, dramatically alter the system impedance variation with frequency. Capacitors do not create harmonics, but severe harmonic distortion can sometimes be attributed to their presence. While the reactance of inductive components increases proportionately to frequency, capacitive reactance XC decreases proportionately:

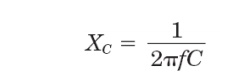
C is the capacitance in farads. This quantity is seldom readily available for power capacitors, which are rated in terms of kvar or Mvar at a given voltage. The equivalent line-to- neutral capacitive reactance at fundamental frequency for a capacitor bank can be determined by

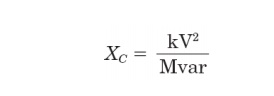
For three-phase banks, use phase-to-phase voltage and the three phase reactive power rating. For single-phase units, use the capacitor voltage rating and the reactive power rating. For example, for a three phase, 1200-kvar, 13.8-kV capacitor bank, the positive-sequence reactance in ohms would be

Parallel resonance

All circuits containing both capacitances and inductances have one or more natural frequencies. When one of those frequencies lines up with a frequency that is being produced on the power system, a resonance may develop in which the voltage and current at that frequency continue to persist at very high values. This is the root of most problems with harmonic distortion on power systems. Figure 4.20 shows a distribution system with potential parallel resonance problems. From the perspective of harmonic sources the shunt capacitor appears in parallel with the equivalent system inductance (source and transformer inductances) at harmonic frequencies as depicted in Fig. 4.21b. Furthermore, since the power system is assumed to have an equivalent voltage source of fundamental frequency only, the power system voltage source appears short circuited in the figure. Parallel resonance occurs when the reactance of XC and the distribution system cancel each other out. The frequency at which this phenomenon occurs is called the parallel resonant frequency. It can be expressed as follows:

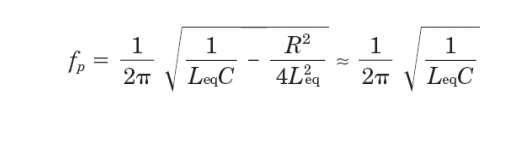
At the resonant frequency, the apparent impedance of the parallel combination of the equivalent inductance and capacitance as seen from the harmonic current source becomes very large.

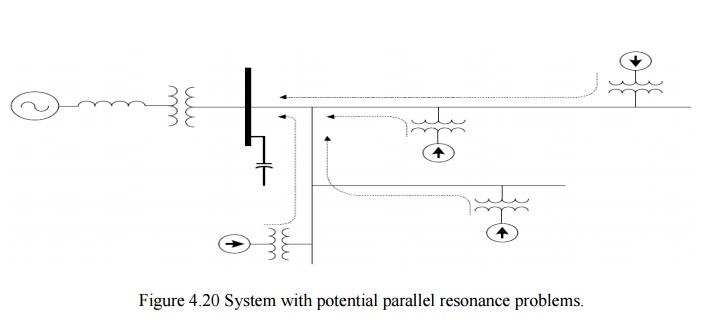
Where Q _ XL/R _ XC/R and R XLeq. Keep in mind that the reactance in this equation are computed at the resonant frequency.

Q often is known as the quality factor of a resonant circuit that determines the sharpness of the frequency response. Q varies considerably by location on the power system. It might be less than 5 on a distribution feeder and more than 30 on the secondary bus of a large step-down transformer. From Eq. (5.22), it is clear that during parallel resonance, a small harmonic current can cause a large voltage drop across the apparent impedance, i.e., Vp = Q XLeq I_h. The voltage near the capacitor bank will be magnified and heavily distorted. Let us now examine current behavior during the parallel resonance. Let the current flowing in the capacitor bank or into the power system be I resonance; thus,

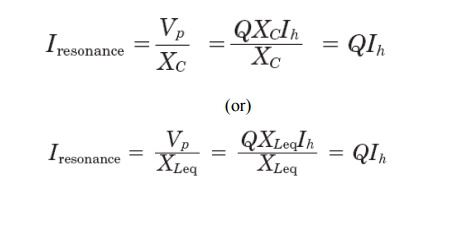
From Eq. It is clear that currents flowing in the capacitor bank and in the power system (i.e., through the transformer) will also be magnified Q times. This phenomenon wills likely cause capacitor failure, fuse blowing, or transformer overheating.

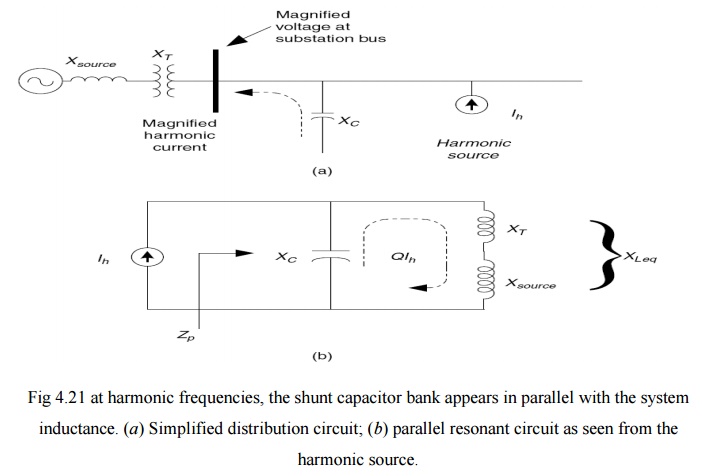
Fig 4.21 at harmonic frequencies, the shunt capacitor bank appears in parallel with the system inductance. (a) Simplified distribution circuit; (b) parallel resonant circuit as seen from the harmonic source.

The extent of voltage and current magnification is determined by the size of the shunt capacitor bank. Fig 4.22 shows the effect of varying capacitor size in relation to the transformer on the impedance seen from the harmonic source and compared with the case in which there is no capacitor. The following illustrates how the parallel resonant frequency is computed. Power systems analysts typically do not have L and C readily available and prefer to use other forms of this relationship. They commonly compute the resonant harmonic hr based on fundamental frequency impedances and ratings using one of the following:

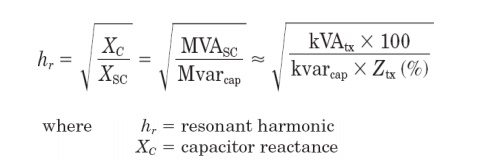
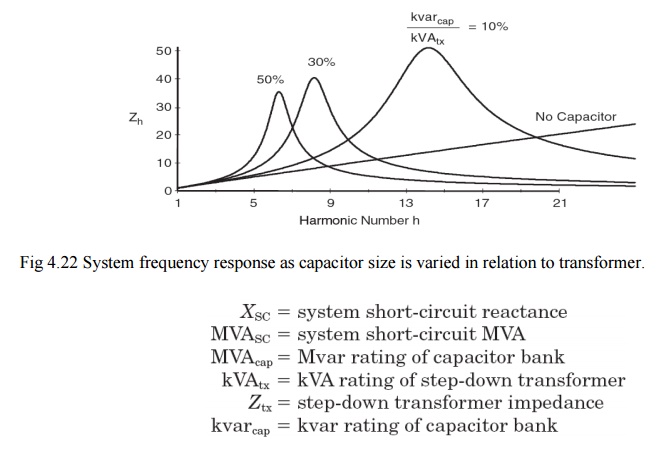
For example, for an industrial load bus where the transformer impedance is dominant, the resonant harmonic for a 1500-kVA, 6 percent transformer and a 500-kvar capacitor bank is approximately

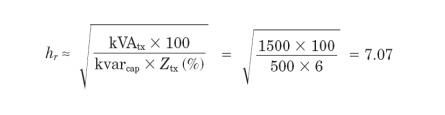
4. Series resonance

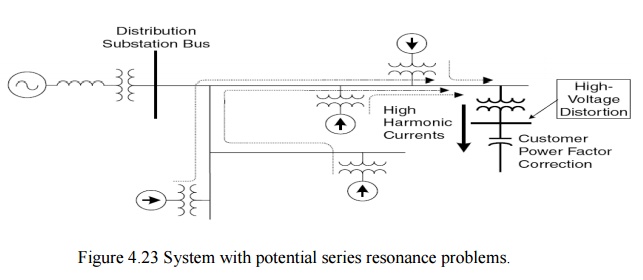
There are certain instances when a shunt capacitor and the inductance of a transformer or distribution line may appear as a series LC circuit to a source of harmonic currents. If the resonant frequency corresponds to a characteristic harmonic frequency of the nonlinear load, the LC circuit will attract a large portion of the harmonic current that is generated in the distribution system. A customer having no nonlinear load, but utilizing power factor correction capacitors, may in this way experience high harmonic voltage distortion due to neighboring harmonic sources. This situation is depicted in Fig. 4.23.

During resonance, the power factor correction capacitor forms a series circuit with the transformer and harmonic sources. The simplified circuit is shown in Fig. 4.24. The harmonic source shown in this figure represents the total harmonics produced by other loads. The inductance in series with the capacitor is that of the service entrance transformer. The series combination of the transformer inductance and the capacitor bank is very small (theoretically zero) and only limited by its resistance. Thus the harmonic current corresponding to the resonant frequency will flow freely in this circuit. The voltage at the power factor correction capacitor is magnified and highly distorted. This is apparent from the following equation:

where Vh and Vs are the harmonic voltage corresponding to the harmonic current Ih and the voltage at the power factor capacitor bank, respectively. The resistance R of the series resonant circuit is not shown in Fig. 4.24, and it is small compared to the reactance.

The negligible impedance of the series resonant circuit can be exploited to absorb desired harmonic currents. This is indeed the principle in designing a notch filter. In many systems with potential series resonance problems, parallel resonance also arises due to the circuit topology. One of these is shown in Fig. 4.24 where the parallel resonance is formed by the parallel combination between X source and a series between XT and XC. The resulting parallel resonant frequency is always smaller than its series resonant frequency due to the source inductance contribution. The parallel resonant frequency can be represented by the following equation: