Effects of Harmonics

Effects of Harmonics:

1. Introduction

Harmonics in electrical system result in waveform distortion. The are periodic disturbance in voltage and current. Any noon sinusoidal periodic waveforms can be considered as combination of sine waveform of certain frequency, amplitude and phase angle. Generally these are individual multiple of fundamental frequency. Hence 3^rd order frequency has got frequency of 150 Hz, and the 5^th order harmonic has 250 frequency and so on. The amplitude and phase angle of individual components will vary depending on the nature of distorted waveform.

THD is defined as the ratio of the root mean square value of the harmonic content to root mean square value of the fundamental quantity, expressed as percent of the fundamental. It is measured of effective value of harmonic distortion.

The  total  harmonic  value  of  distortion  (THD)  is  the  value  used  to  describe  the characteristics of distorted waveform. The THD is a measured of how badly the waveform is distorted from pure sinusoidal the THD is 0%. IEEE standard 519 recommends that for most system, the THD of the bus voltage should be less than 5% with maximum of 3% with any individual components.

2. Harmonic Distortion

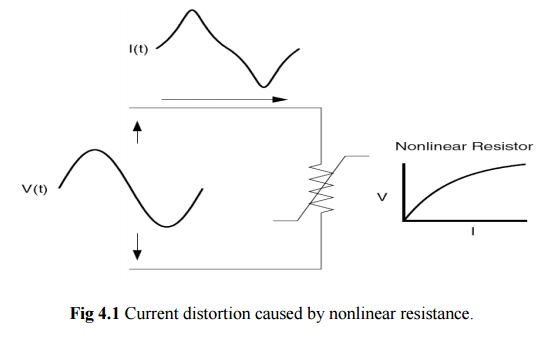
Harmonic distortion is caused by nonlinear devices in the power system. A nonlinear device is one in which the current is not proportional to the applied voltage. Figure 4.1 illustrates this concept by the case of a sinusoidal voltage applied to a simple nonlinear resistor in which the voltage and current vary according to the curve shown. While the applied voltage is perfectly sinusoidal, the resulting current is distorted. Increasing the voltage by a few percent may cause the current to double and take on a different wave shape. This is the source of most harmonic distortion in a power system.

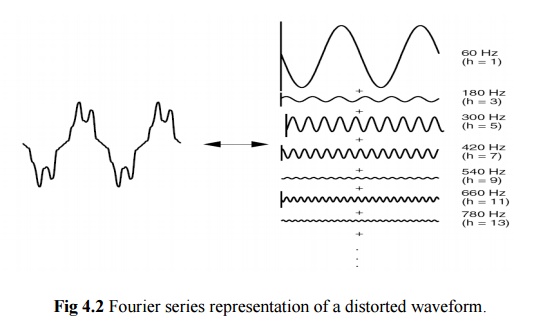
Figure 4.2 illustrates that any periodic, distorted waveform can be expressed as a sum of sinusoids. When a waveform is identical from one cycle to the next, it can be represented as a sum of pure sine waves in which the frequency of each sinusoid is an integer multiple of the fundamental frequency of the distorted wave. This multiple is called a harmonic of the fundamental, hence the name of this subject matter. The sum of sinusoids is referred to as a

Fourier series, named after the great mathematician who discovered the concept.

Because of the above property, the Fourier series concept is universally applied in analyzing harmonic problems. The system can now be analyzed separately at each harmonic. In addition, finding the system response of a sinusoid of each harmonic individually is much more straightforward compared to that with the entire distorted waveforms. The outputs at each frequency are then combined to form a new Fourier series, from which the output waveform may be computed, if desired. Often, only the magnitudes of the harmonics are of interest.

When both the positive and negative half cycles of a waveform have identical shapes, the Fourier series contains only odd harmonics. This offers a further simplification for most power system studies because most common harmonic-producing devices look the same to both polarities. In fact, the presence of even harmonics is often a clue that there is something wrong— either with the load equipment or with the transducer used to make the measurement. There are notable exceptions to this such as half-wave rectifiers and arc furnaces when the arc is random.

Usually, the higher-order harmonics (above the range of the 25th to 50th, depending on the system) are negligible for power system analysis. While they may cause interference with low-power electronic devices, they are usually not damaging to the power system. It is also difficult to collect sufficiently accurate data to model power systems at these frequencies.

A common exception to this occurs when there are system resonances in the range of frequencies. These resonances can be excited by notching or switching transients in electronic power converters. This causes voltage waveforms with multiple zero crossings which disrupt timing circuits. These resonances generally occur on systems with underground cable but no power factor correction capacitors.

If the power system is depicted as series and shunt elements, as is the conventional practice, the vast majority of the nonlinearities in the system are found in shunt elements (i.e., loads). The series impedance of the power delivery system (i.e., the short-circuit impedance between the source and the load) is remarkably linear. In transformers, also, the source of harmonics is the shunt branch (magnetizing impedance) of the common “T” model; the leakage impedance is linear. Thus, the main sources of harmonic distortion will ultimately be end-user loads. This is not to say that all end users who experience harmonic distortion will themselves have significant sources of harmonics, but that the harmonic distortion generally originates with some end-user’s load or combination of loads.

3. Voltage versus Current Distortion

The word harmonics is often used by itself without further qualification. For example, it is common to hear that an adjustable-speed drive or an induction furnace can’t operate properly because of harmonics. What does that mean? Generally, it could mean one of the following

Three things:

1.  The harmonic voltages are too great (the voltage too distorted) for the control to properly determine firing angles.

2.  The harmonic currents are too great for the capacity of some device in the power supply system such as a transformer, and the machine must be operated at a lower than rated power.

3. The harmonic voltages are too great because the harmonic currents produced by the device are too great for the given system condition.

As suggested by this list, there are separate causes and effects for voltages and currents as well as some relationship between them. Thus, the term harmonics by itself is inadequate to definitively describe a problem.

Nonlinear loads appear to be sources of harmonic current in shunt with and injecting harmonic currents into the power system. For nearly all analyses, it is sufficient to treat these harmonic-producing loads simply as current sources. There are exceptions to this as will be described later.

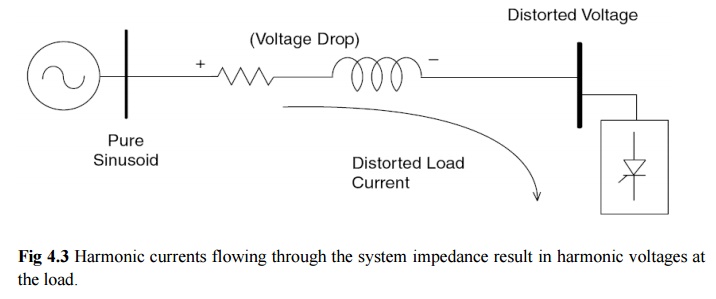
As Fig. 4.3 shows, voltage distortion is the result of distorted currents passing through the linear, series impedance of the power delivery system, although, assuming that the source bus is ultimately a pure sinusoid, there is a nonlinear load that draws a distorted current. The harmonic currents passing through the impedance of the systemcause a voltage drop for each harmonic. This results in voltage harmonics appearing at the load bus. The amount of voltage distortion depends on the impedance and the current. Assuming the load bus distortion stays within reasonable limits (e.g., less than 5 percent), the amount of harmonic current produced by the load is generally constant.

While the load current harmonics ultimately cause the voltage distortion, it should be noted that load has no control over the voltage distortion. The same load put in two different locations on the power system will result in two different voltage distortion values. Recognition of this fact is the basis for the division of responsibilities for harmonic control that are found in standards such as IEEE Standard 519-1992, Recommended Practices and Requirements for

Harmonic Control in Electrical Power Systems:

1. The control over the amount of harmonic current injected into the system takes place at the end-use application.

2. Assuming the harmonic current injection is within reasonable limits, the control over the voltage distortion is exercised by the entity having control over the system impedance, which is often the utility.

One must be careful when describing harmonic phenomena to understand that there are distinct differences between the causes and effects of harmonic voltages and currents. The use of the term harmonics should be qualified accordingly. By popular convention in the power industry, the majority of times when the term is used by itself to refer to the load apparatus, the speaker is referring to the harmonic currents. When referring to the utility system, the voltages are generally the subject. To be safe, make a habit of asking for clarification.

4. Harmonic Indices:

The two most commonly used indices for measuring the harmonic content of a waveform are the total harmonic distortion and the total demand distortion. Both are measures of the effective value of a waveform and may be applied to either voltage or current.

5. Total harmonic distortion(THD)

The THD is a measure of the effective value of the harmonic components of a distorted waveform. That is, it is the potential heating value of the harmonics relative to the fundamental. This index can be calculated for either voltage or current:

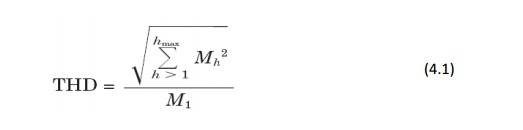
where Mh is the rms value of harmonic component h of the quantity M.

The rms value of a distorted waveform is the square root of the sum of the squares as shown in Eqs. (4.1) and (4.2). The THD is related to the rms value of the waveform as follows:

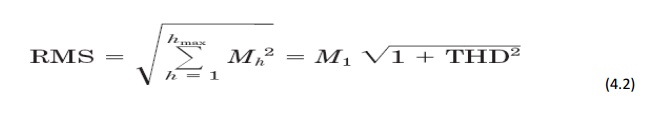
The THD is a very useful quantity for many applications, but its limitations must be realized. It can provide a good idea of how much extra heat will be realized when a distorted voltage is applied across a resistive load. Likewise, it can give an indication of the additional losses caused by the current flowing through a conductor. However, it is not a good indicator of the voltage stress within a capacitor because that is related to the peak value of the voltage waveform, not its heating value.

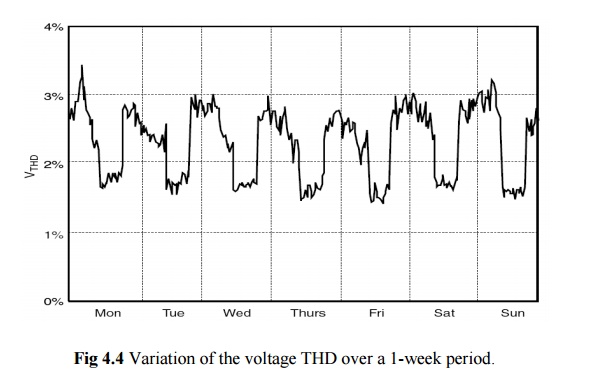
The THD index is most often used to describe voltage harmonic distortion. Harmonic voltages are almost always referenced to the fundamental value of the waveform at the time of the sample. Because fundamental voltage varies by only a few percent, the voltage THD is nearly always a meaningful number. Variations in the THD over a period of time often follow a distinct pattern representing nonlinear load activities in the system. Figure 4.4 shows the voltage THD variation over a 1-week period where a daily cyclical pattern is obvious. The voltage THD shown in Fig. 4.4 was taken at a 13.2-kV distribution substation supplying a residential load. High-voltage THD occurs at night and during the early morning hours since the nonlinear loads are relatively high compared to the amount of linear load during these hours. A 1-week observation period is often required to come up with a meaningful THD pattern since it is usually the shortest period to obtain representative and reproducible measurement results.

6. Total demand distortion(TDD)

Current distortion levels can be characterized by a THD value, as has been described, but this can often be misleading. A small current may have a high THD but not be a significant threat to the system. For example, many adjustable-speed drives will exhibit high THD values for the input current when they are operating at very light loads. This is not necessarily a significant concern because the magnitude of harmonic current is low, even though its relative current distortion is high.

Some analysts have attempted to avoid this difficulty by referring THD to the fundamental of the peak demand load current rather than the fundamental of the present sample. This is called total demand distortion and serves as the basis for the guidelines in IEEE Standard 519-1992, Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems. It is defined as follows:

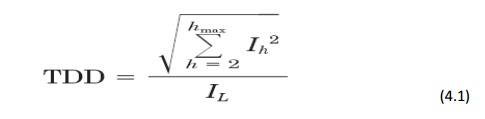
I_L is the peak, or maximum, demand load current at the fundamental frequency component measured at the point of common coupling (PCC). There are two ways to measure I_L. With a load already in the system, it can be calculated as the average of the maximum demand current for the preceding 12 months. The calculation can simply be done by averaging the 12-month peak demand readings. For a new facility, I_L has to be estimated based on the predicted load profiles.