Polynomial Arithmetic

POLYNOMIAL ARITHMETIC

Before continuing our discussion of finite fields, we need to introduce the interest- ing subject of polynomial arithmetic. We are concerned with polynomials in a single variable x, and we can distinguish three classes of polynomial arithmetic.

•                           Ordinary polynomial arithmetic, using the basic rules of algebra.

•                           Polynomial arithmetic in which the arithmetic on the coefficients is performed modulo p ; that is, the coefficients are in  GF(p).

•                 Polynomial arithmetic in which the coefficients are in GF(p), and the polynomials are defined modulo a polynomial m(x) whose highest power is some integer  n.

This section examines the first two classes, and the next section covers the   last class.

Ordinary  Polynomial Arithmetic

A polynomial of degree n (integer n >= 0) is an expression of the form

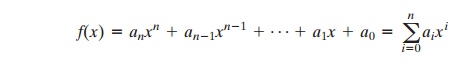
where the ai are elements of some designated set of numbers S, called the coefficient set, and an != 0. We say that such polynomials are defined over the coefficient set S.

A zero-degree polynomial is called a constant polynomial and is simply an element of the set of coefficients. An nth-degree polynomial is said to be a monic polynomial if an = 1.

In the context of abstract algebra, we are usually not interested in evaluating a

polynomial for a particular value of x [e.g., f(7)]. To emphasize this point, the variable

x is sometimes referred to as the indeterminate.

Polynomial arithmetic includes the operations of addition, subtraction, and multiplication. These operations are defined in a natural way as though the variable x was an element of S. Division is similarly defined, but requires that S be a field. Examples of fields include the real numbers, rational numbers, and Zp for p prime. Note that the set of all integers is not a field and does not support polynomial division.

Addition and subtraction are performed by adding or subtracting corresponding coefficients. Thus, if

In the last formula, we treat ai as zero for i > n and bi as zero for i  >  m. Note that  the degree of the product is equal to the sum of the degrees of the two polynomials.

As an example, let f(x) = x3 + x2 + 2 and g(x) = x2 - x + 1, where S is the set of integers. Then

f(x) + g(x)  = x3 + 2x2 - x + 3

f(x) - g(x) = x3 + x + 1

f(x) * g(x)  = x5 + 3x2 - 2x +  2

Figures 4.3a through 4.3c show the manual calculations. We comment on division subsequently.

Polynomial Arithmetic with Coefficients in  Zp

Let us now consider polynomials in which the coefficients are elements of some  field F; we refer to this as a polynomial over the field F. In that case, it is easy to show that the set of such polynomials is a ring, referred to as a polynomial ring.  That is, if we consider each distinct polynomial to be an element of the set, then     that set is a  ring.

When polynomial arithmetic is performed on polynomials over a field, then division is possible. Note that this does not mean that exact division is possible. Let  us clarify this distinction. Within a field, given two elements a and b, the quotient a/bis also an element of the field. However, given a ring R that is not a field, in

general, division will result in both a quotient and a remainder; this is not exact division.

Consider the division 5/3 within a set S. If S is the set of rational numbers, which is a field, then the result is simply expressed as 5/3 and is an element of S. Now suppose that S is the field Z7. In this case, we calculate (using Table 4.5c)

5/3 = (5 * 3 - 1) mod 7 = (5 * 5) mod 7 =  4

which is an exact solution. Finally, suppose that S is the set of integers, which is a ring but not a field. Then 5/3 produces a quotient of 1 and a remainder    of 2:

5/3  =  1  + 2/3

5  = 1  * 3  + 2

Thus, division is not exact over the set of integers

Now, if we attempt to perform polynomial division over a coefficient set that is not a field, we find that division is not always  defined.

If the coefficient set is the integers, then (5x2)/(3x) does not have a solution, because it would require a coefficient with a value of 5/3, which is not in the coef- ficient set. Suppose that we perform the same polynomial division over Z7. Then we have (5x2)/(3x)  =  4x, which is a valid polynomial over Z7.

However, as we demonstrate presently, even if the coefficient set is a field, poly- nomial division is not necessarily exact. In general, division will produce a quotient and a remainder. We can restate the division algorithm of Equation (4.1) for polynomials over a field as follows. Given polynomials f(x) of degree n and g(x) of degree (m),  (n Ú m), if we divide f(x) by g(x), we get a quotient q(x) and a remainder r(x) that obey  the relationship

With the understanding that remainders are allowed, we can say that polynomial division is possible if the coefficient set is a field.

In an analogy to integer arithmetic, we can write f(x) mod g(x) for the remain- der r(x) in Equation (4.10). That is, r(x) = f(x) mod g(x). If there is no remainder [i.e., r(x) = 0], then we can say g(x) divides f(x), written as g(x) ƒ f(x). Equivalently, we can say that g(x) is a factor of f(x) or g(x) is a divisor of f(x).

For the preceding example [f(x) = x3 + x2 + 2 and g(x) = x2 - x + 1], f(x)/g(x) produces a quotient of q(x) = x + 2 and a remainder r(x) = x, as shown in Figure 4.3d. This is easily verified by noting that

q(x)g(x) + r(x) = (x + 2)(x2 - x + 1) + x = (x3 + x2 - x + 2) + x

= x3 + x2 + 2  =  f(x)

For  our  purposes,  polynomials over GF(2) are  of  most  interest.  Recall from Section 4.5 that in GF(2), addition is equivalent to the XOR operation, and multi- plication is equivalent to the logical AND operation. Further, addition and subtraction are equivalent mod 2: 1 + 1 = 1 - 1 = 0; 1 + 0 = 1 - 0 = 1; 0 + 1 = 0 - 1 = 1.

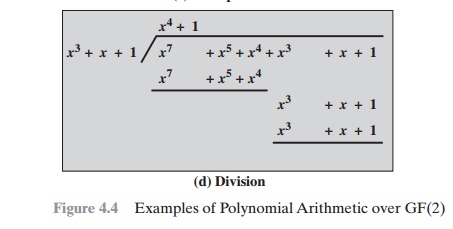
Figure 4.4 shows an example  of  polynomial  arithmetic  over  GF(2).  For  f(x) = (x7 + x5 + x4 + x3 + x + 1) and g(x) = (x3 + x + 1), the figure shows   f(x) + g(x); f(x) - g(x); f(x) * g(x); and f(x)/g(x). Note that g(x)| f(x).

A polynomial f(x) over a field F is called irreducible if and only if f(x) cannot be expressed as a product of two polynomials, both over F, and both of degree lower than that of f(x). By analogy to integers, an irreducible polynomial is also called a prime polynomial.

The polynomial9 f(x)  =  x4  +  1 over  GF(2) is reducible, because

x4  + 1  =  (x  + 1)(x3  + x2  + x  + 1).

Consider the polynomial f(x)  = x3  + x  + 1. It is clear by inspection that x is not   a factor of f(x). We easily show that x  +  1 is not a factor of f(x):

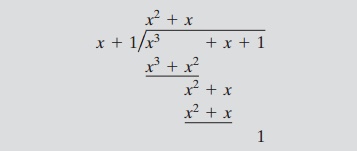
Thus, f(x) has no factors of degree 1. But it is clear by inspection that if f(x) is reducible, it must have one factor of degree 2 and one factor of degree 1. Therefore, f(x) is irreducible.

Finding the Greatest Common Divisor

We can extend the analogy between polynomial arithmetic over a field and integer arithmetic by defining the greatest common divisor as follows. The polynomial c(x) is said to be the greatest common divisor of a(x) and b(x) if the following are true.

1.                        c(x) divides both a(x) and b(x).

2.                        Any divisor of a(x) and b(x) is a divisor of c(x).

An equivalent definition is the following: gcd[a(x), b(x)] is the polynomial of maximum degree that divides both a(x) and b(x).

We can adapt the Euclidean algorithm to compute the greatest common divi- sor of two polynomials. The equality in Equation (4.6) can be rewritten as the fol- lowing theorem.

gcd[a(x), b(x)]  = gcd[b(x), a(x) mod b(x)]     (4.11)

Equation (4.11) can be used repetitively to determine the greatest common divisor. Compare the following scheme to the definition of the Euclidean algorithm for integers.

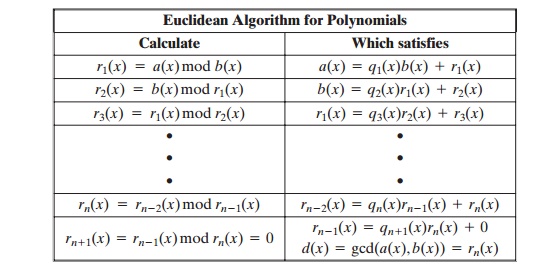
At each iteration, we have d(x) = gcd(ri + 1(x), ri(x)) until finally d(x) = gcd(rn(x), 0) = rn(x). Thus, we can find the greatest common divisor of two integers by repetitive application of the division algorithm. This is the Euclidean algorithm  for polynomials. The algorithm assumes that the degree of a(x) is greater than the degree of b(x).

Summary

We began this section with a discussion of arithmetic with ordinary polynomials. In ordinary polynomial arithmetic, the variable is not evaluated; that is, we do not plug a value in for the variable of the polynomials. Instead, arithmetic operations are per- formed on polynomials (addition, subtraction, multiplication, division) using the ordinary rules of algebra. Polynomial division is not allowed unless the coefficients are elements of a field.

Next, we discussed polynomial arithmetic in which the coefficients are elements of GF(p). In this case, polynomial addition, subtraction, multiplication, and division are allowed. However, division is not exact; that is, in general division results in a quotient and a remainder.

Finally, we showed that the Euclidean algorithm can be extended to find the greatest common divisor of two polynomials whose coefficients are elements of a field. All of the material in this section provides a foundation for the following section, in which polynomials are used to define finite fields of order pn.