The Euclidean Algorithm

THE EUCLIDEAN ALGORITHM

One of the basic techniques of number theory is the Euclidean algorithm, which is a simple procedure for determining the greatest common divisor of two positive integers. First, we need a simple definition: Two integers are relatively prime if their only common positive integer factor is 1.

Greatest Common Divisor

Recall that nonzero b is defined to be a divisor of a if a = mb for some m, where a, b, and m are integers. We will use the notation gcd(a, b) to mean the greatest common divisor of a and b. The greatest common divisor of a and b is the largest integer that divides both a and b. We also define gcd(0, 0) = 0.

More formally, the positive integer c is said to be the greatest common divisor of a and b if

1.                                       c is a divisor of a and of  b.

2.                                       Any divisor of a and b is a divisor of c. An equivalent definition is the  following:

gcd(a, b)  =  max[k, such that k | a and k |  b]

Because we require that the greatest common divisor be positive, gcd(a, b) =

gcd(a, -b)  =  gcd( -a, b)  =  gcd( -a,-b). In general, gcd(a, b)  =  gcd( | a | , | b | ).

gcd(60, 24)  =  gcd(60, -24)  = 12

Also, because all nonzero integers divide 0, we have gcd(a, 0)  =     | a | .

We stated that two integers a and b are relatively prime if their only common positive integer factor is 1. This is equivalent to saying that a and b are relatively prime if gcd(a, b)  = 1.

8 and 15 are relatively prime because the positive divisors of 8 are 1, 2, 4, and 8, and the positive divisors of 15 are 1, 3, 5, and 15. So 1 is the only integer on both lists.

Finding the Greatest Common Divisor

We now describe an algorithm credited to Euclid for easily finding the greatest common divisor of two integers. This algorithm has significance subsequently in this chapter. Suppose we have integers a, b such that d = gcd(a, b). Because gcd( | a | , | b | )  =   gcd(a, b), there is no harm in assuming a  >= b  > 0. Now dividing a by b and applying the division algorithm, we can state:

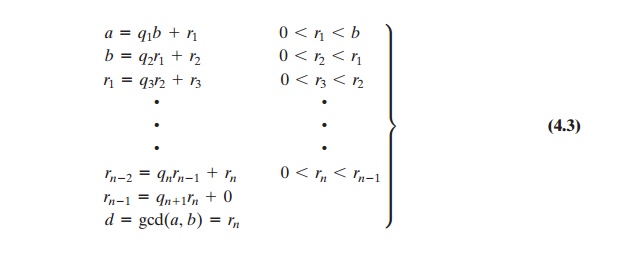
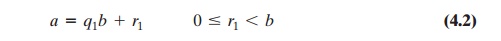
At each iteration, we have d = gcd(ri, ri + 1) until finally d = gcd(rn, 0) = rn. Thus, we can find the greatest common divisor of two integers by repetitive application of the division algorithm. This scheme is known as the Euclidean algorithm.

We have essentially argued from the top down that the final result is the gcd(a, b). We  can also argue from the bottom up. The  first step is  to  show that    rn  divides  a  and  b. It  follows  from  the  last  division  in  Equation  (4.3) that rn divides rn - 1. The  next to last division shows  that rn divides rn – 2 because it divides both terms on the right. Successively, one sees that rn divides all ri’s and finally a and b. It remains to show that rn is the largest divisor that divides a and b. If we take any arbitrary integer that divides a and b, it must also divide r1, as explained previously. We can follow the sequence of equations in Equation (4.3) down and show that c  must divide all  ri’s. Therefore c  must divide rn, so  that   rn  = gcd(a, b).

Let us now look at an example with relatively large numbers to see the power of this algorithm:

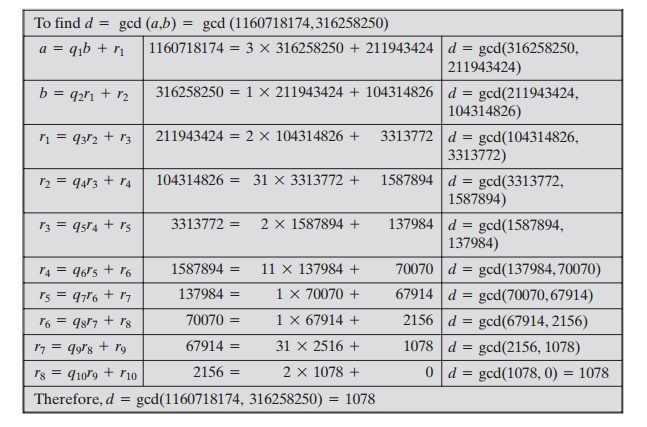
In this example, we begin by dividing 1160718174 by 316258250, which gives 3 with a remainder of 211943424. Next we take 316258250 and divide it by 211943424. The process continues until we get a remainder of 0, yielding a result of  1078.

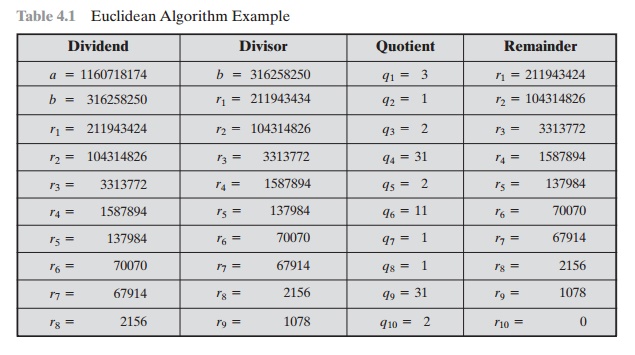
It will be helpful in what follows to recast the above computation in tabular form. For every step of the iteration, we have ri - 2 = qiri - 1 + ri, where ri - 2 is the dividend, ri - 1 is the divisor, qi is the quotient, and ri is the remainder. Table 4.1 summarizes the results.

Table 4.1  Euclidean Algorithm Example