Modular Arithmetic

MODULAR ARITHMETIC

The Modulus

If a is an integer and n is a positive integer, we define a mod n to be the remainder when a is divided by n. The integer n is called the modulus. Thus, for any integer a, we can rewrite Equation (4.1) as  follows:

a  = qn + r 0 <= r < n; q =   [a/n ]

a  =  [a/n ] * n  + (a mod n)

11 mod 7 = 4;      - 11 mod 7 = 3

Two  integers a  and  b  are said to  be  congruent modulo n, if  (a mod n) = (b mod n). This is written as a K b (mod n).2

73 ‚ 4 (mod 23);        21 ‚ -9 (mod 10)

Note that if a K 0 (mod n), then n | a.

Properties of Congruences

Congruences have the following properties:

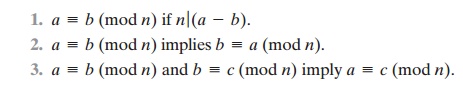
To demonstrate the first point, if n | (a  - b), then (a  - b)  = kn for some k.

So we can write a = b + kn. Therefore, (a mod n) = (remainder when b + kn is divided by n)  =  (remainder when b is divided by n)  =  (b mod n).

23  = = 8 (mod 5)   because       23 - 8 = 15 = 5 *  3

-11 = = 5 (mod 8)   because       -11 - 5 =  -16 = 8 * (-2)

81  ==  0 (mod 27) because       81 - 0 = 81 = 27 *  3

The remaining points are as easily proved.

Modular Arithmetic Operations

Note that, by definition (Figure 4.1), the (mod n) operator maps all integers into the set of integers {0, 1, ... , (n - 1)}. This suggests the question: Can we perform arithmetic operations within the confines of this set? It turns out that we can; this technique is known as modular arithmetic.

Modular arithmetic exhibits the following properties:

1.                                                   [(a mod n)  + (b mod n)] mod n  = (a  + b) mod n

2.                                                   [(a mod n) - (b mod n)] mod n = (a - b) mod n

3.                                                   [(a mod n) * (b mod n)] mod n = (a * b) mod n

We demonstrate the first property. Define (a mod n)  =  ra and (b mod n)  =  rb.

Then we can write a  = ra  + jn for some integer j and b  = rb  +   kn for some integer

k.             Then

(a  + b) mod n  = (ra  + jn  + rb   +    kn) mod n

= (ra  + rb  + (k  + j)n) mod n

= (ra  + rb) mod  n

= [(a mod n)  + (b mod n)]mod n

The remaining properties are proven as easily. Here are examples of the three properties:

11 mod 8  =  3; 15 mod 8  = 7

[(11 mod 8)  + (15 mod 8)] mod 8  = 10 mod 8  = 2

(11  + 15) mod 8  = 26 mod 8  = 2

[(11 mod 8) - (15 mod 8)] mod 8 = -4 mod 8 = 4

(11 - 15) mod 8 = -4 mod 8 = 4

[(11 mod 8) * (15 mod 8)] mod 8 = 21 mod 8 = 5

(11 * 15) mod 8 = 165 mod 8 =  5

Exponentiation is performed by repeated multiplication, as in ordinary arith- metic. (We have more to say about exponentiation in Chapter 8.)

To find 117 mod 13, we can proceed as follows:

112  =  121  K  4 (mod 13)

114  =  (112)2  K  42  K 3 (mod 13)

117  K 11  * 4  * 3  K 132  K 2 (mod 13)

Thus, the rules for ordinary arithmetic involving addition, subtraction, and multiplication carry over into modular arithmetic.

Table 4.2 provides an illustration of modular addition and multiplication modulo 8. Looking at addition, the results are straightforward, and there is a regular pattern to the matrix. Both matrices are symmetric about the main diagonal in conformance to the commutative property of addition and multiplication. As in ordinary addition, there is an additive inverse, or negative, to each integer in modu- lar arithmetic. In this case, the negative of an integer x is the integer y such   that

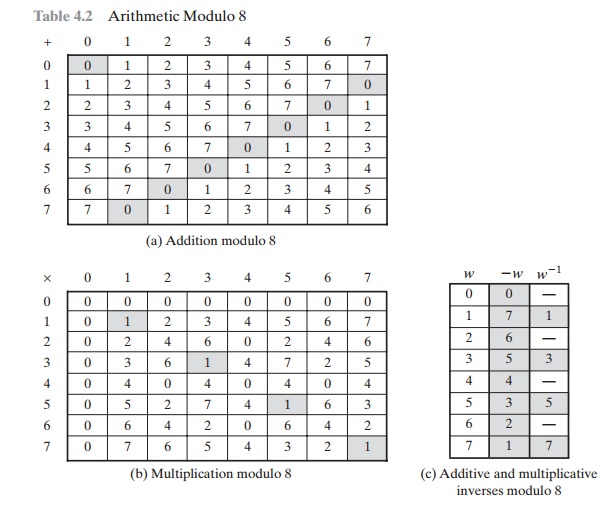
(x + y) mod 8 = 0. To find the additive inverse of an integer in the left-hand column, scan across the corresponding row of the matrix to find the value 0; the integer at the top of that column is the additive inverse; thus, (2 + 6) mod 8 = 0. Similarly, the entries in the multiplication table are straightforward. In ordinary arithmetic, there is a multiplicative inverse, or reciprocal, to each integer. In modular arithmetic mod 8, the multiplicative inverse of x is the integer y such that (x * y) mod 8 = 1 mod 8. Now, to find the multiplicative inverse of an integer from the multiplication table, scan across the matrix in the row for that integer to find the value 1; the integer at the top of that column is the multiplicative inverse; thus, (3 * 3) mod 8 = 1. Note that not all integers mod 8 have a multiplicative inverse; more about that later.

Properties of Modular Arithmetic

Define the set Zn as the set of nonnegative integers less than n:

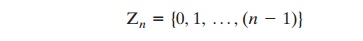
This is referred to as the set of residues, or residue classes (mod n). To be more precise, each integer in Zn represents a residue class. We can label the residue classes (mod n) as

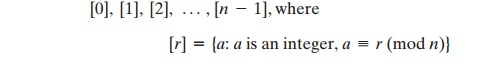
The residue classes (mod 4) are

[0] = { ... , -16, -12, -8, -4, 0, 4, 8, 12, 16, ... }

[1] = { ... , -15, -11, -7, -3, 1, 5, 9, 13, 17, ... }

[2] = { ... , -14, -10, -6, -2, 2, 6, 10, 14, 18, ... }

[3] = { ... , -13, -9, -5, -1, 3, 7, 11, 15, 19, ... }

Of all the integers in a residue class, the smallest nonnegative integer is the one used to represent the residue class. Finding the smallest nonnegative integer to which k is congruent modulo n is called reducing k modulo n.

If we perform modular arithmetic within Zn, the properties shown in Table 4.3 hold for integers in Zn. We show in the next section that this implies that Zn is a com- mutative ring with a multiplicative identity element.

There is one peculiarity of modular arithmetic that sets it apart from ordinary arithmetic. First, observe that (as in ordinary arithmetic) we can write the following:

if (a  + b)  K (a  + c) (mod n)   then   b  K c (mod n)              (4.4)

(5  + 23)  K (5  + 7) (mod 8);  23  K   7(mod 8)

Equation (4.4) is consistent with the existence of an additive inverse. Adding the additive inverse of a to both sides of Equation (4.4), we have

((-a)  +  a  +  b)  K  ((-a)  +  a  +  c) (mod n) b  K c (mod n)

However, the following statement is true only with the attached condition:

if (a  * b)  K (a  * c) (mod n) then b  K c (mod n)   if a is relatively prime to n  (4.5)

Recall that two integers are relatively prime if their only common positive integer factor is 1. Similar to the case of Equation (4.4), we can say that Equation (4.5) is

Table 4.3 Properties of Modular Arithmetic for Integers in Zn

consistent with the existence of a multiplicative inverse. Applying the multiplicative inverse of a to both sides of Equation (4.5), we  have

((a - 1)ab) K ((a - 1)ac) (mod n) b K c (mod n)

To see this, consider an example in which the condition of Equation (4.5) does not hold. The integers 6 and 8 are not relatively prime, since they have the common factor 2. We have the following:

6 * 3 = 18 K 2 (mod 8)

6 * 7 = 42 K 2 (mod 8)

Yet 3 [ 7 (mod 8).

The reason for this strange result is that for any general modulus n, a multiplier a that is applied in turn to the integers 0 through (n - 1) will fail to produce a complete set of residues if a and n have any factors in common.

With a  =  6 and n  = 8,

Because  we  do  not  have  a  complete  set  of  residues  when  multiplying  by 6, more  than  one  integer  in  Z₈  maps  into  the  same  residue.  Specifically, 6 * 0 mod 8 = 6 * 4 mod 8; 6 * 1 mod 8 = 6 * 5 mod 8; and so on. Because this is a many-to-one mapping, there is not a unique inverse to the multiply operation. However, if we take a  =  5 and n  =     8, whose only common factor is 1,

However, if we take a  =  5 and n  =     8, whose only common factor is 1,

The line of residues contains all the integers in Z8, in a different order.

In general, an integer has a multiplicative inverse in Zn if that integer is relatively prime to n. Table 4.2c shows that the integers 1, 3, 5, and 7 have a multiplicative inverse in Z8; but 2, 4, and 6 do not.

Euclidean Algorithm Revisited

The Euclidean algorithm can be based on the following theorem: For any nonnegative integer a and any positive integer b,

gcd(a, b)  =   gcd(b, a  mod b)                (4.6)

gcd(55, 22) =  gcd(22, 55 mod 22) =  gcd(22, 11) =   11

To see that Equation (4.6) works, let  d  =  gcd(a, b). Then, by the definition of  gcd, d |  a and d |       b. For any positive integer b, we can express a as

a = kb  + r  K r (mod b)  a mod b  = r

with k, r integers.Therefore, (a mod b) = a - kb for some integer k. But because d | b, it also divides kb.We also have d | a.Therefore, d | (a mod b).This shows that d is a common divisor of b and (a mod b). Conversely, if d is a common divisor of b and (a mod b), then d | kb and thus d | [kb + (a mod b)], which is equivalent to d | a.Thus, the set of common divisors of a and b is equal to the set of common divisors of b and (a mod b).Therefore, the gcd of one pair is the same as the gcd of the other pair, proving the  theorem.

Equation (4.6) can be used repetitively to determine the greatest common divisor.

gcd(18, 12)  = gcd(12, 6)  = gcd(6, 0)  = 6

gcd(11, 10)  = gcd(10, 1)  = gcd(1, 0)  = 1

This is the same scheme shown in Equation (4.3), which can be rewritten in the following way.

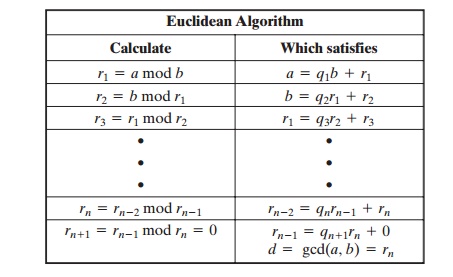
We can define the Euclidean algorithm concisely as the following recursive function.

Euclid(a,b)

if (b=0) then return a;

else return Euclid(b, a mod b);

The Extended Euclidean Algorithm

We now proceed to look at an extension to the Euclidean algorithm that will be impor- tant for later computations in the area of finite fields and in encryption algorithms, such as RSA. For given integers a and b, the extended Euclidean algorithm not only calculate the greatest common divisor d but also two additional integers x and y that satisfy the following equation.

ax  + by  = d  =  gcd(a,  b)            (4.7)

It should be clear that x and y will have opposite signs. Before examining the algorithm, let us look at some of the values of x and y when a = 42 and b  =  30.  Note that gcd(42, 30)  =  6. Here is a partial table of values3 for 42x  + 30y.

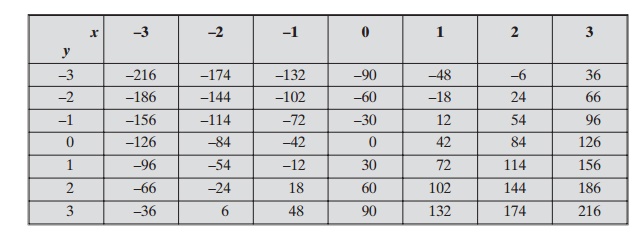
Observer that all of the entries are divisible by 6. This is not surprising, because  both  42  and  30  are  divisible  by  6,  so  every  number  of  the    form 42x  + 30y  = 6(7x  + 5y) is a multiple of 6. Note also that  gcd(42, 30)  = 6   appears in the table. In general, it can be shown that for given integers a and b, the smallest positive value of ax  +  by is equal to gcd(a, b).

Now let us show how to extend the Euclidean algorithm to determine (x, y, d) given a and b. We again go through the sequence of divisions indicated in Equation (4.3), and we assume that at each step  i  we can find integers  xi  and  yi  that satisfy   ri  = axi  + byi. We end up with the following sequence.

We need to make several additional comments here. In each row, we calculate a new remainder ri based on the remainders of the previous two rows, namely ri - 1 and ri - 2. To start the algorithm, we need values for r0 and r- 1, which are just a and b. It is then straightforward to determine the required values for x - 1, y- 1, x0, and y0.

We know from the original Euclidean algorithm that the process ends with a remainder  of  zero  and  that  the  greatest  common  divisor  of  a   and  b     is d = gcd(a, b) = rn. But we also have determined that Therefore, in Equation (4.7), x  =  xn and y  = yn. 

d  = rn  = axn  + byn.

As   an   example,   let   us  use a  = 1759 and b  = 550 and   solve  for 1759x + 550y = gcd(1759, 550). The results are shown in Table 4.4. Thus, we have 1759 x (–111) + 550 x 355 = –195249 + 195250 = 1.

Table 4.4  Extended Euclidean Algorithm Example

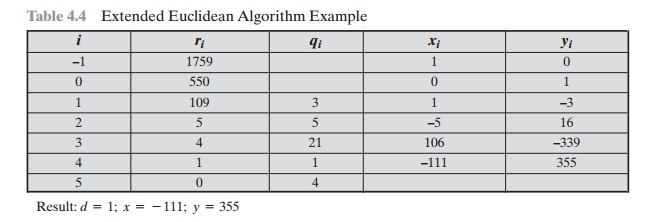
Result: d = 1; x =  - 111; y =   355