Groups, Rings, and Fields

GROUPS, RINGS, AND FIELDS

Groups, rings, and fields are the fundamental elements of a branch of mathematics known as abstract algebra, or modern algebra. In abstract algebra, we are concerned with sets on whose elements we can operate algebraically; that is, we can combine two elements of the set, perhaps in several ways, to obtain a third element of the set. These operations are subject to specific rules, which define the nature of the set. By convention, the notation for the two principal classes of operations on set elements is usually the same as the notation for addition and multiplication on ordinary num- bers. However, it is important to note that, in abstract algebra, we are not limited to ordinary arithmetical operations. All this should become clear as we proceed.

Groups

A group G, sometimes denoted by {G, # }, is a set of elements with a binary operation

denoted by # that associates to each ordered pair (a, b) of elements in G an element

(a # b) in G, such that the following axioms are obeyed:

If a group has a finite number of elements, it is referred to as a finite group, and the order of the group is equal to the number of elements in the group. Otherwise, the group is an infinite group.

A group is said to be abelian if it satisfies the following additional condition:

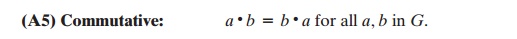
The set of integers (positive, negative, and 0) under addition is an abelian group. The set of nonzero real numbers under multiplication is an abelian group. The set Sn from the preceding example is a group but not an abelian group for n > 2.

When the group operation is addition, the identity element is 0; the   inverse element   of   a   is   –a;  and   subtraction   is   defined   with   the   following rule: 

a  - b  = a  + (-b).

CYCLIC GROUP We  define exponentiation within a group as a repeated appli- cation of the group operator,  so that a3 = a a a. Furthermore, we define a0 = e as the identity element, and  a - n  =  (a')n, where  a'  is the inverse element of  a within the group. A group G is cyclic if every element of G is a power ak (k is an integer) of a fixed element a H G. The element a is said to generate the group G    or to be a generator of G. A cyclic group is always abelian and may be finite or infinite.

The additive group of integers is an infinite cyclic group generated by the element 1. In this case, powers are interpreted additively, so that n is the nth power of 1.

Rings

A ring R, sometimes denoted by {R,  +,  *}, is a set of elements with two binary operations, called addition and multiplication,6 such that for all a, b, c in R the following  axioms  are  obeyed.

In  essence,  a  ring  is  a  set  in  which  we  can  do  addition,  subtraction [a - b = a + (-b)], and multiplication without leaving the set.

With respect to addition and multiplication, the set of all n-square matrices over the real numbers is a ring.

A ring is said to be commutative if it satisfies the following additional condition:

(M4) Commutativity of multiplication: ab = ba for all a, b in R.

Let S be the set of even integers (positive, negative, and 0) under the usual opera- tions of addition and multiplication. S is a commutative ring. The set of all n-square matrices defined in the preceding example is not a commutative ring.

The set Zn of integers {0, 1, ... , n - 1}, together with the arithmetic operations modulo n, is a commutative ring (Table 4.3).

Next, we define an integral domain, which is a commutative ring that obeys the following axioms.

(M5) Multiplicative identity: There is an element 1 in R such that a1  = 1a  = a for all a in  R.

(M6) No zero divisors: If a, b in R and ab  = 0, then either a  = 0 or b  = 0.

Let S be the set of integers, positive, negative, and 0, under the usual operations of addition and multiplication. S is an integral domain.

Fields

A field F, sometimes denoted by {F,  +,  x}, is a set of elements with two binary opera- tions, called addition and multiplication, such that for all a, b, c in F the following axioms are obeyed.

(A1–M6) F is an integral domain; that is, F satisfies axioms A1 through A5 and M1 through M6.

(M7) Multiplicative inverse:  For each a in F, except 0, there is an element

a - 1 in F such that aa - 1 = (a - 1)a = 1.

In essence, a field is a set in which we can do addition, subtraction, multiplication, and division without leaving the set. Division is defined with the following rule: a/b = a(b - 1).

Familiar examples of fields are the rational numbers, the real numbers, and the complex numbers. Note that the set of all integers is not a field, because not every element of the set has a multiplicative inverse; in fact, only the elements 1 and –1 have multiplicative inverses in the integers.

Figure 4.2 summarizes the axioms that define groups, rings, and fields.