Chapter:
Finite Fields Of The Form GF(p)
FINITE FIELDS OF
THE FORM GF(p)
In
Section 4.4, we defined a field as a set that obeys all of the axioms of Figure
4.2 and gave some examples of infinite fields. Infinite fields are not of
particular interest in the context of cryptography. However, finite fields play
a crucial role in many cryptographic algorithms. It can be shown that the order
of a finite field (number of elements in the field) must be a power of a prime pn,
where n is a positive integer.
We
discuss prime numbers in detail in Chapter 8. Here, we need only say that a
prime number is an integer whose only positive integer factors are itself and
1. That is, the only positive integers that are divisors of p are p
and 1.
The
finite field of order pn is generally written GF(pn);
GF stands for Galois field, in honor of the mathematician who first studied
finite fields. Two special cases are of interest for our purposes. For n
= 1, we have the finite field GF(p); this finite field has a different
structure than that for finite fields with n 7 1 and is studied in this
section. In Section 4.7, we look at finite fields of the form GF(2n).
Finite
Fields of Order p
For a
given prime, p, we define the finite field of order p, GF(p),
as the set Zp of integers {0, 1, ..... , p - 1}
together with the arithmetic operations modulo p.
Recall
that we showed in Section 4.3 that the set Zn of integers {0,
1, ..... , n - 1}, together with the arithmetic operations modulo n,
is a commuta-tive ring (Table 4.3). We further observed that any integer in Zn
has a multiplicative inverse if and only if that integer is relatively prime to
n [see discussion of Equation (4.5)]7 If n is prime,
then all of the nonzero integers in Zn are relatively prime
to n, and therefore there exists a multiplicative inverse for all of the
nonzero integers in Zn. Thus, for Zp we can
add the following properties to those listed in Table 4.3:

Because w is
relatively prime to p, if we multiply all the elements of Zp
by w, the resulting residues are all of the elements of Zp
permuted. Thus, exactly one of the residues has the value 1. Therefore, there
is some integer in Zp that, when multiplied by w,
yields the residue 1. That integer is the multiplicative inverse of w,
designated w - 1.Therefore, Zp
is in fact a finite field. Furthermore, Equation (4.5) is consistent with
the existence of a multiplicative inverse and can be rewritten without the
condition:

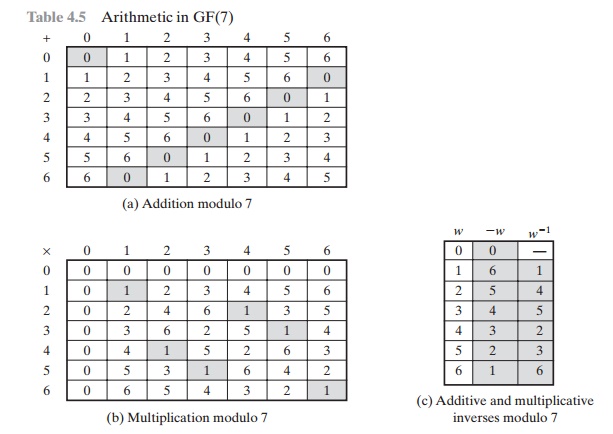
Table 4.5
shows arithmetic operations in GF(7). This is
a field of order 7 using modular arithmetic modulo 7. As can be seen, it
satisfies all of the properties required of a field (Figure 4.2). Compare this
table with Table 4.2. In the latter case, we see that the set Z8,
using modular arithmetic modulo 8, is not a field. Later in this chapter,
we show how to define addition and multiplication operations on Z8 in such
a way as to form
a finite field.
Finding the
Multiplicative Inverse in GF(p)
It is easy to find the multiplicative inverse of an element in GF(p) for small
values of
p.
You simply construct a multiplication table,
such as shown
in Table 4.5b, and the
desired result can be read directly.
However, for large values of p, this approach is not practical.
Table 4.5
Arithmetic in
GF(7)
If a and b are relatively prime, then
b has a multiplicative inverse modulo a. That
is, if gcd(a, b)
= 1, then b has a multiplicative inverse
modulo a. That is,
for positive integer b 6 a,
there exists a b - 1 6 a such
that bb - 1 = 1
mod a. If a is a prime number and b 6 a,
then clearly a and b are relatively prime and have a
greatest common divisor of 1. We now
show that we can easily compute b - 1 using
the extended Euclidean algorithm.
We repeat here Equation (4.7), which we showed can be solved with the
extended Euclidean algorithm:
ax + by =
d =
gcd(a, b)
Now, if gcd(a, b) = 1, then
we have ax + by = 1. Using the basic equalities of mod- ular arithmetic, defined in Section
4.3, we can say
[(ax mod a)
+ (by mod a)] mod a =
1 mod a
0 + (by mod a) = 1
But if by mod a = 1, then y = b - 1. Thus, applying the extended Euclidean
algorithm to Equation (4.7) yields the value of the multiplicative inverse of b if
gcd(a, b) = 1. Consider the example that was shown in Table 4.4.
Here we have a = 1759, which is a prime number,
and b = 550. The solution of the equation 1759x + 550y = d yields a value of y = 355. Thus, b - 1 = 355. To
verify, we calculate 550 355 mod 1759 = 195250 mod 1759 = 1.
More generally, the extended Euclidean algorithm can be used to find a
multi- plicative inverse in Zn for any n. If we apply the extended Euclidean algorithm to the equation nx + by = d, and the algorithm yields d = 1, then y = b - 1 in Zn.
Summary
In this section, we have shown how to construct a finite field of order p, where p is prime. Specifically, we defined GF(p) with the following properties.
1.
GF(p)
consists of p elements.
2.
The binary operations + and x are defined
over the set. The operations of addi-
tion, subtraction, multiplication, and division can be performed without leav- ing
the set. Each element of the set other than 0 has a multiplicative inverse.
We have shown that the elements of GF(p) are the integers {0, 1, ..... , p - 1} and
that the arithmetic operations are addition and multiplication mod p.