Chapter: Cryptography and Network Security Principles and Practice : One Symmetric Ciphers : Basic Concepts in Number Theory and Finite Fields
Divisibility and the Division Algorithm
DIVISIBILITY
AND THE DIVISION ALGORITHM
Divisibility
We say that a nonzero b divides a if
a = mb for some m, where
a,
b,
and m are integers. That is, b divides
a if there is no remainder on division. The notation b | a is commonly used to mean b divides a. Also, if b | a, we say that b is a divisor of a.

Subsequently, we will need some simple
properties of divisibility for integers, which are as follows:


The Division
Algorithm
Given any positive integer
n
and any nonnegative integer a, if we divide a by
n, we get an integer quotient q
and an integer remainder r that
obey the following relationship:
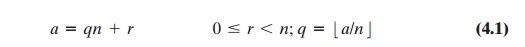
where |x | is the largest
integer less than
or equal to x. Equation (4.1)
is referred to as the division algorithm.
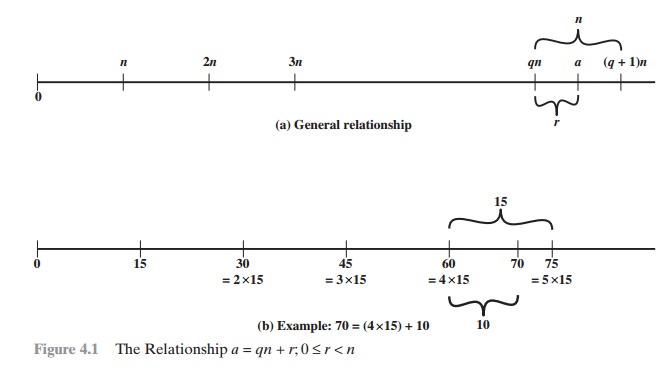
Figure 4.1a demonstrates that, given a and positive
n, it is always possible to find q and r that satisfy the preceding relationship. Represent the integers on the number line; a will
fall somewhere on that
line (positive a is shown, a similar
demonstration can be made for negative
a). Starting at 0, proceed to n, 2n, up to qn, such that qn <=a and(q + 1)n >
a. The distance
from qn to a is r, and we have
found the unique values of q and r. The remainder r is often
referred to as a residue.
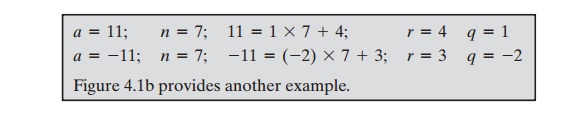
Related Topics