Plastic Analysis Of Structures

PLASTIC ANALYSIS OF STRUCTURES

1. Statically indeterminate axial problems

In these analyses we used superposition often, knowing that for a linearly elastic structure it was valid. However, an elastic analysis does not give information about the loads that will actually collapse a structure. An indeterminate structure may sustain loads greater than the load that first causes a yield to occur at any point in the structure.

In fact, a structure will stand as long as it is able to find redundancies to yield. It is only when a structure has exhausted all of its redundancies will extra load causes it to fail. Plastic analysis is the method through which the actual failure load of a structure is calculated, and as will be seen, this failure load can be significantly greater than the elastic load capacity.

To summarize this, Prof. Seande Courcy (UCD) used to say: 'a structure only collapses when it has exhausted all means of standing'.

Before analyzing complete structures, we review material and cross section behavior beyond the elastic limit.

2. Beams in pure bending

2.1. Material Behavior

Auniaxial tensile stress on a ductile material such as mild  steel typically provides the following graph of stress versus strain:

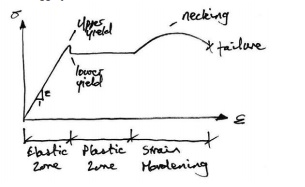
As can be seen, the material can sustain strains farinexcess of the strain at which yield occurs before failure. This property of the material is called its ductility. Though complex models do exist to accurately reflect the above real behavior of the material, the most common, and simplest, model is the idealized stress-strain curve. This is the curve for an ideal elastic-plastic material (which doesn't exist), and the graph is:

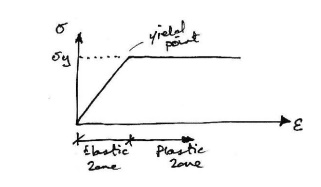
As can be seen, once the yield has been reached it is taken that an indefinite amount of strain can occur. Since so much post-yield strain is modeled, the actual material (or cross section) must also be capable of allowing such strains. That is, it must be sufficiently ductile for the idealized stress-strain curve to bevalid. Next we consider the behavior of across section of an ideal elastic-plastic material subject to bending. In doing so, we seek the relationship between applied moment and the rotation (or more accurately, the curvature) of across section.

2.2. Moment-Rotation Characteristics of General Cross Section

We consider an arbitrary cross-section with a vertical plane of symmetry, which is also the plane of loading. We consider the cross section subject to an increasing bending moment, and assess the stresses at each stage.

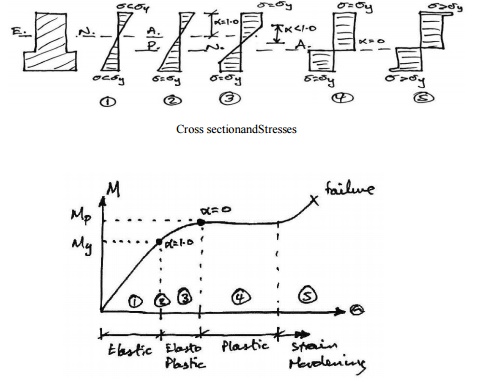
Stage1- Elastic Behaviour

The applied moment causes stresses over the cross-section that are all less than the yield stress of the material.

Stage2-Yield Moment

The applied moment is just sufficient that the yield stress of the material is reached at the outer most fibre(s) of the cross-section. All other stresses in the cross section are less than the yield stress. This is limit of applicability of an elastic analysis and of elastic design. Since all fibres are elastic, the ratio of the depth of the elastic to plastic regions,

Stage3- Elasto-Plastic Bending

The moment applied to the cross section has been increased beyond the yield moment. Since by the idealized stress-strain curve the material cannot sustain a stress greater than yield stress, the fibres at the yield stress have progressed inwards towards the centre of the beam. Thus over the cross section the reisanelastic core and a plastic region. The ratio of the depth of the elastic core to the plastic region is .

Since extra moment is being applied and no stress is bigger than the yield stress, extra rotation of  the section occurs: the moment-rotation curve losses its linearity and curves, giving more rotation per unit moment (i.e. looses stiffness).

Stage4- Plastic Bending

The applied moment to the cross section is such that all fibres in the cross section are at yield stress. This is termed the Plastic Moment Capacity of the section since there are no fibres at an elastic stress, Also note that the full plastic moment requires an infinite strain at the neutral axis

And so is physically impossible to achieve. However, it is closely approximated in practice. Any attempt at increasing the moment at this points imply results in more rotation, once the cross-section has sufficient ductility. There fore in steel members the cross section classification must be plastic and in concrete members the section must be under-reinforced.

Stage5-Strain Hardening

Due to strain hardening of the material, a small amount of extra moment can be sustained.

The above moment-rotation curve represents the behavior of across section of a regular elastic-plastic material. However, it is usually further simplified as follows:

With this idealized moment-rotation curve, the cross section linearly sustains moment up to the plastic moment capacity of the section and then yields in rotation an indeterminate amount. Again, to use this idealization, the actual section must be capable of sustaining large rotations- that is it must be ductile.

Analysis of Rectangular Cross Section

Since we now know that across section can sustain more load than just the yield moment, we are interested in how much more. In other words we want to find the yield moment and plastic moment, and we do so for a rectangular section. Taking the stress diagrams from those of the moment-rotation curve examined previously, we have:

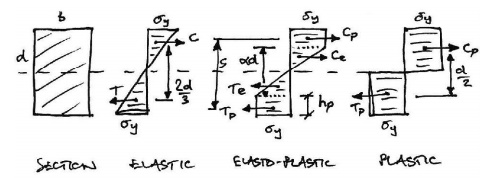
3. Shape Factor

Thus the ratio of elastic to plastic moment capacity is:

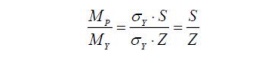
This ratio is termed the shape factor,f, and is a property of across section alone. For a rectangular cross-section, we have:

And so a rectangular section can sustain 50% more moment than the yield moment, before a plastic hinge is formed. Therefore the shape factor is a good measure of the efficiency of across section In bending. Shape factors for some other cross sections are

4. Plastic Hinge

Note that once the plastic moment capacity is reached, the section can rotate freely- that is, it behaves like a hinge, except with moment of M patthe hinge. This is termed a plastic hinge, and is the basis for plastic analysis. At the plastic hinge stresses remain constant, but strains and hence rotations can increase.

4.1. Methods of Plastic Analysis

1.  The Incremental Method

This is probably the most obvious approach: the loads on the structure are incremented until the first plastic hinge forms. This continues until sufficient hinges have formed to collapse the structure. This is a labour-intensive, 'brute-force', approach, but one that is most readily suited for computer implementation.

2. The Equilibrium (or Statical) Method

In this method, free and reactant bending moment diagrams are drawn. These diagrams are over laid to identify the likely locations of plastic hinges. This method therefore satisfies the equilibrium criterion first leaving the two remaining criterion to derived therefrom.

3.The Kinematic (or Mechanism) Method

In this method, a collapse mechanism is first postulated. Virtual work equations are then written for this collapse state, allowing the calculations of the collapse bending moment diagram. This method satisfies the mechanism condition first, leaving the remaining two criteria to be derived there from.

We will concentrate mainly on the Kinematic Method, but introduce now the Incremental Method to illustrate the main concepts.

4.1.1. Incremental Method

Example1- Propped Cantilever

We now assess the behavior of a simple statically indeterminate structure under increasing load. We consider a propped cantilever with mid-span point load:

Since the peak moments are less than the yield moments, we know that yield stress has not been reached at any point in the beam. Also, the maximum moment occurs at A and so this point will first reach the yield moment.

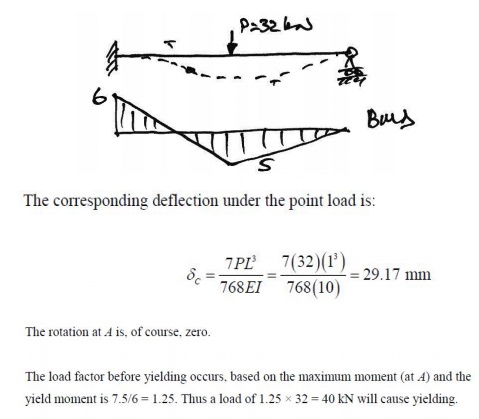
4.1.2. Equilibrium Method

Introduction

To perform this analysis we generally follow the following steps:

1.Find a primary structure by removing redundant until the structure is statically determinate;

2.Draw the primary (or free) bending moment diagram;

3.Draw the reactant BMD for each redundant, as applied to the primary structure;

4.Construct a composite BMD by combing the primary and reactant BMDs;

5.Determine the equilibrium equations from the composite BMD;

6.Choose the points where plastic hinges are likely to form and introduce into the equilibrium equations;

7.Calculate the collapse load factor, or plastic moment capacity as required.

For different possible collapse mechanisms, repeat steps 6 and 7, varying the hinge locations. We now apply this method to the Illustrative Example previously analyzed.

Steps 1 to 3 of the Equilibrium Method are illustrated in the following diagram:

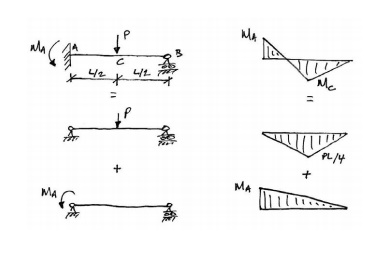
For Step 4, inconstructing the Composite BMD, we arbitrarily choose tension on the underside of the beam as positive. By convention in the Equilibrium Method, instead of drawing the two BMD son opposite sides (as is actually the case), the reactant BMD is drawn 'flipped' over the line and subtracted from the primary BMD: the net remaining area is the final BMD. This is best explained by illustration below:

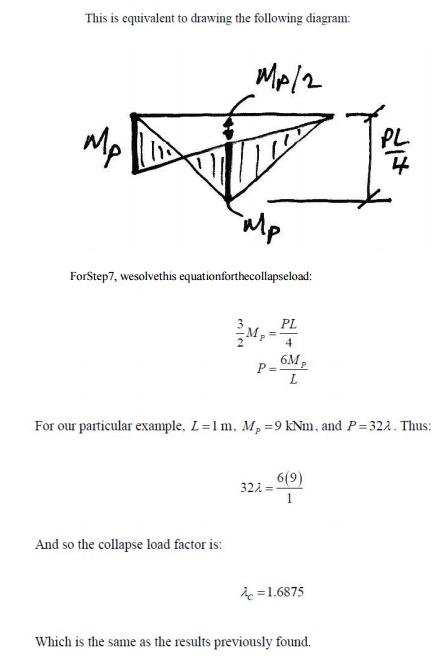
4.1.3 Kinematic Method Using Virtual Work

Introduction

Probably  the easiest way  to carry  out a plastic analysis is through  the Kinematic Method using virtual         work. To do this we allow the presumed shape at collapse to be the compatible displace mentset, and the external loading and internal bending moments to be the equilibrium set. We can then equate  external and internal virtual work, and solve for the collapse load factor for that supposed mechanism.

Remember:

Equilibrium set: the internal bending moments at collapse;

Compatibleset: the virtual collapsed configuration (see below).

Note that in        the actual   collapse configuration   the members will have elastic deformation in between the plastic hinges. However, since a virtual displacement does not have to be real, only compatible, we will choose to ignore the elastic deformations between plastic hinges, and take the members to be straight between them.

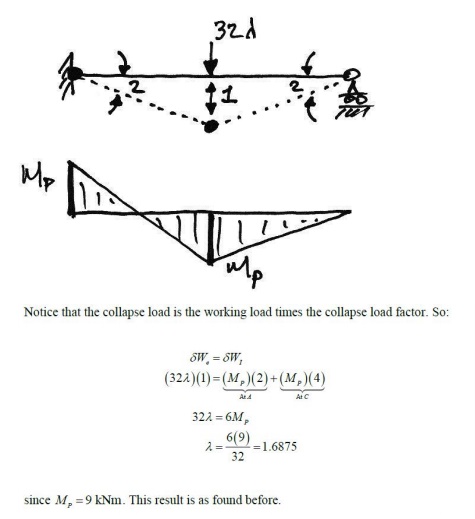
5. Collapse Mechanism

So for our previous beam, we know that we require two hinges for collapse (one more than its degree of redundancy), and we think that the hinges will occur under the points of peak moment, A and C. Therefore impose a unit virtual displacement at C and relate the corresponding virtual rotations of the hinges using,

5.1 Other Collapse Mechanisms

For the collapse mechanism looked at previously, it seemed obvious that the plastic hinge in the span should be beneath the load. But why? Using virtual work we can examine any possible collapse mechanism. So let's consider the following collapse mechanism and see why the plastic hinge has to be located beneath the load.

Plastic Hinge between A and C:

Imposing a unit virtual deflection at B, we get the following collapse mechanism:

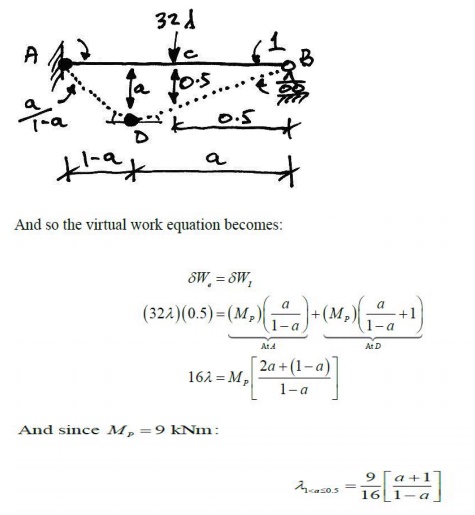
And so we see that the collapse load factor for this mechanism depends on the position of the plastic hinge in the span.

6. Plastic Analysis of Beams

Example2-Fixed-Fixed Beam with Point Load

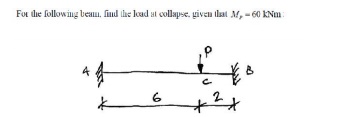
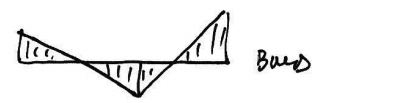
To start the problem, we examine the usual elastic BMD to see where the plastic hinges are likely to form:

We also need to know how many hinges are required. This structure is 3? statically indeterminate and so we might expect the number of plastic hinges required to be 4. However, since one of the indeterminacies is horizontal restraint, removing it would not change the bending behavior of the beam.

Thus for a bending collapse only 2 indeterminacies apply and so it will only take 3 plastic hinges to cause collapse. So looking at the elastic BMD, we'll assume a collapse mechanism with the 3 plastic hinges at the peak moment locations: A, B, and C.

And so the applied load is in equilibrium with the free BMD of the collapse BMD.

2. Mechanism:

From the proposed  collapse mechanism it is apparent that the beam is a mechanism.

3. Yield:

From the collapse BMD it can be seen that now here is exceeded. PM Thus the solution meets the three conditions and so, by the Uniqueness Theorem, is the correct solution.

Example 3- Propped Cantilever with Two Point Loads

For the following beam, for a load factor of 2.0, find the required plastic moment capacity:

Once again we try to picture possible failure mechanisms. Since maximum moments occur underneath point loads, there are two real possibilities:

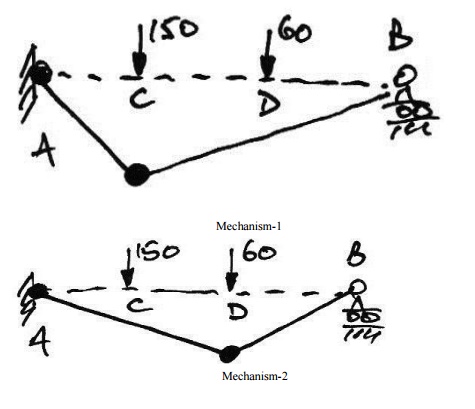
Therefore, we analyse both and apply the Upper bound Theorem to find the design plastic moment capacity.

Mechanism1: Plastic Hingeat C:

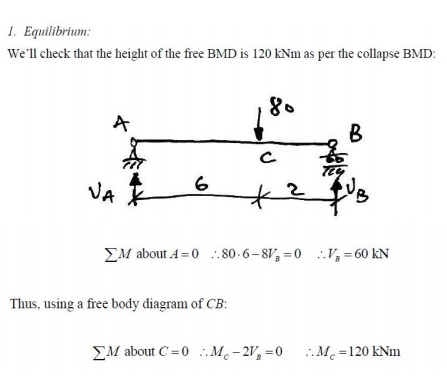
1. Equilibrium:

Using the BMD at collapse, we'll check that the height of the free BMD is that of the equivalents imply-supported beam. Firstly the collapse BMD from Mechanism1 is:

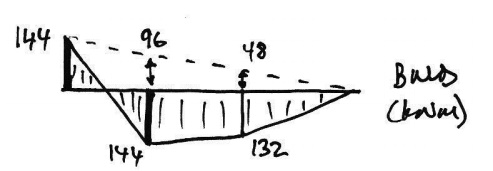
Hence, the total heights of the free BMD are:

Checking these using a simply-supported beam analysis

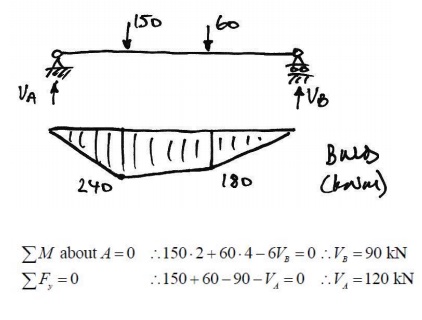
Thus, using appropriate free body diagrams of AC and DB:

And so the applied load is in equilibrium with the free BMD of the collapse BMD.

2. Mechanism:

From the proposed collapse mechanism it is apparent that the beam is a mechanism. Also, since it is a propped cantilever and thus one degree indeterminate, we require two plastic hinges for collapse, and these we have

3.Yield:

From the collapse BMD it can be seen that no where is the design exceeded. 144kNm Thus by the Uniqueness Theorem we have the correct solution. Lastly, we'll examine why the Mechanism 2 collapse is not the correct solution. Since the virtual work method provides an upper bound, then, by the Uniqueness Theorem, it must not be the correct solution because it must violate the yield condition. Using the collapse Mechanism 2 to determine reactions, we can draw the following BMD for collapse Mechanism 2:

From this it is apparent that Mechanism 2 is not the unique solution, and so the design plastic moment capacity must be 144 kNmasimplied previously from the Upper bound Theorem.

4.Basic Collapse Mechanisms:

In frames, the basic mechanisms of collapse are:

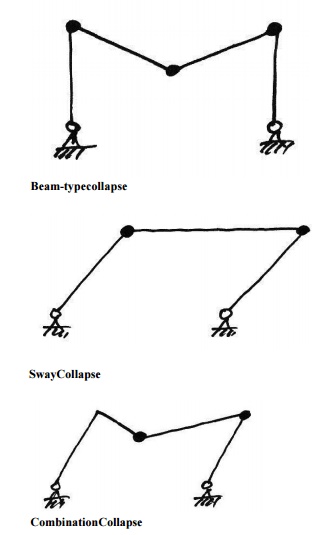
5. Combination of Mechanisms

One of the most powerful tools in plastic analysis is Combination of Mechanisms. This allows us to work out the virtual work equations for the beamandsway collapses separately and then combine them to find the collapse load factor for a combination collapse mechanism.

Combination of mechanisms is based  on the idea that  there are only a certain  number of independent equilibrium equations for a structure. Any further equations are obtained from a combination of these independent equations. Since equilibrium equations can be obtained using

virtual work applied to a possible collapse mechanism, it follows that there are independent collapse mechanisms, andother collapse mechanisms that may be obtained form a combination of the independent collapse mechanisms.

6. Simple Portal Frame

In this example we will consider a basic prismatic (so all members have the same plastic moment capacity) rectangular portal frame with pinned feet:

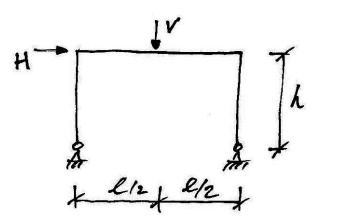
We will consider this general cases  othatwecaninferthe properties and behavior of all such frames. We will consider each of the possible mechanisms outlined above.

7.Beam collapse:

The possible beam collapse looks as follows:

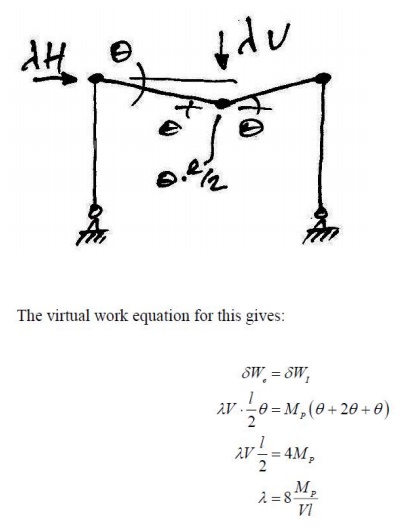
7.Collapse Mode

Since we don't know the relative values of H and V, we cannot determine the correct collapse mode. However, we can identify these collapse modes if we plot the three load factor equations derived above on the following interaction chart:

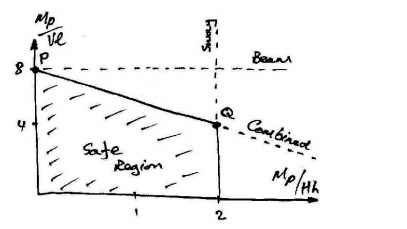
Notice that each mechanism defines a boundary and that it is only the region inside all of these boundaries that is safe. Now, for a given ration of V to H, we will be able to determine the critical collapse mechanism. Note also that the beam collapse mechanism is only critical for this frame at point P on the chart- this point is also included in the Combined mechanism. The bending moment diagrams corresponding to each of the mechanisms are approximately:

An interesting phenomenon is observed at point Q on the chart, where the Sway and Combined mechanisms give the same result. Looking at the bending moment diagrams, we can see that this occurs as the moment at the top of the left column becomes equal to the mid-span moment of the beam:

8. Upper bound (Unsafe) Theorem:

This can be stated as:

If a bending moment diagram is found which satisfies the conditions of equilibrium and mechanism (but not necessarily yield), then the corresponding load factor is either greater than or equal to the true load factor at collapse.

This is called the unsafe theorem because for an arbitrarily assumed mechanism the load factor is either exactly right (when the yield criterionismet) or is wrong and is too large, leading a designer to think that the frame can carry more load than is actually possible.

9. Lower bound (Safe)Theorem:

If a bending moment diagram is found which satisfies the conditions of equilibrium and yield (but not necessarily that of mechanism), then the corresponding load factor is either less than or equal to the true load factor at collapse