Plastic Hinge

Plastic Hinge

Note that once the plastic moment capacity is reached, the section can rotate freely- that is, it behaves like a hinge, except with moment of M patthe hinge. This is termed a plastic hinge, and is the basis for plastic analysis. At the plastic hinge stresses remain constant, but strains and hence rotations can increase.

1. Methods of Plastic Analysis

1.  The Incremental Method

This is probably the most obvious approach: the loads on the structure are incremented until the first plastic hinge forms. This continues until sufficient hinges have formed to collapse the structure. This is a labour-intensive, 'brute-force', approach, but one that is most readily suited for computer implementation.

2. The Equilibrium (or Statical) Method

In this method, free and reactant bending moment diagrams are drawn. These diagrams are over laid to identify the likely locations of plastic hinges. This method therefore satisfies the equilibrium criterion first leaving the two remaining criterion to derived therefrom.

3.The Kinematic (or Mechanism) Method

In this method, a collapse mechanism is first postulated. Virtual work equations are then written for this collapse state, allowing the calculations of the collapse bending moment diagram. This method satisfies the mechanism condition first, leaving the remaining two criteria to be derived there from.

We will concentrate mainly on the Kinematic Method, but introduce now the Incremental Method to illustrate the main concepts.

1.1. Incremental Method

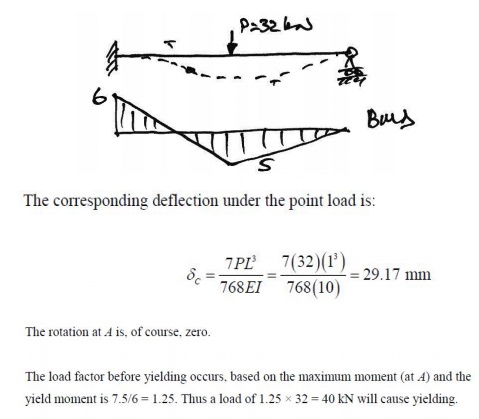
Example1- Propped Cantilever

We now assess the behavior of a simple statically indeterminate structure under increasing load. We consider a propped cantilever with mid-span point load:

Since the peak moments are less than the yield moments, we know that yield stress has not been reached at any point in the beam. Also, the maximum moment occurs at A and so this point will first reach the yield moment.

1.2. Equilibrium Method

Introduction

To perform this analysis we generally follow the following steps:

1.Find a primary structure by removing redundant until the structure is statically determinate;

2.Draw the primary (or free) bending moment diagram;

3.Draw the reactant BMD for each redundant, as applied to the primary structure;

4.Construct a composite BMD by combing the primary and reactant BMDs;

5.Determine the equilibrium equations from the composite BMD;

6.Choose the points where plastic hinges are likely to form and introduce into the equilibrium equations;

7.Calculate the collapse load factor, or plastic moment capacity as required.

For different possible collapse mechanisms, repeat steps 6 and 7, varying the hinge locations. We now apply this method to the Illustrative Example previously analyzed.

Steps 1 to 3 of the Equilibrium Method are illustrated in the following diagram:

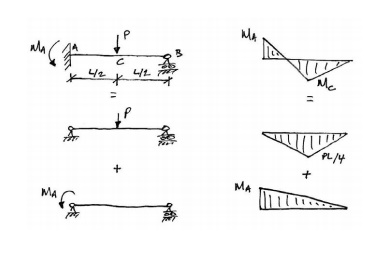
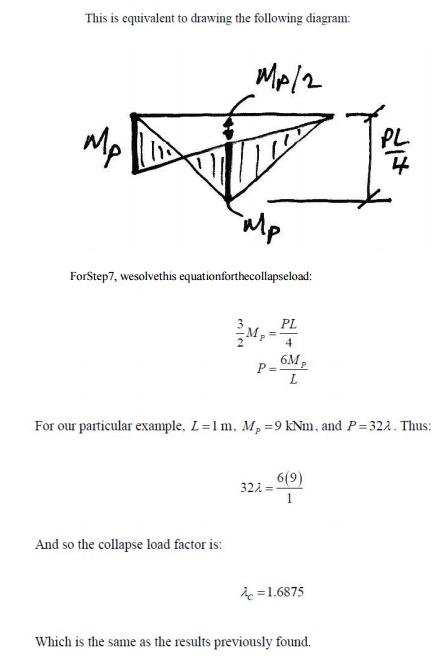
For Step 4, inconstructing the Composite BMD, we arbitrarily choose tension on the underside of the beam as positive. By convention in the Equilibrium Method, instead of drawing the two BMD son opposite sides (as is actually the case), the reactant BMD is drawn 'flipped' over the line and subtracted from the primary BMD: the net remaining area is the final BMD. This is best explained by illustration below:

1.3 Kinematic Method Using Virtual Work

Introduction

Probably  the easiest way  to carry  out a plastic analysis is through  the Kinematic Method using virtual         work. To do this we allow the presumed shape at collapse to be the compatible displace mentset, and the external loading and internal bending moments to be the equilibrium set. We can then equate  external and internal virtual work, and solve for the collapse load factor for that supposed mechanism.

Remember:

Equilibrium set: the internal bending moments at collapse;

Compatibleset: the virtual collapsed configuration (see below).

Note that in        the actual   collapse configuration   the members will have elastic deformation in between the plastic hinges. However, since a virtual displacement does not have to be real, only compatible, we will choose to ignore the elastic deformations between plastic hinges, and take the members to be straight between them.