Plastic Analysis of Beams

Plastic Analysis of Beams

Example2-Fixed-Fixed Beam with Point Load

To start the problem, we examine the usual elastic BMD to see where the plastic hinges are likely to form:

We also need to know how many hinges are required. This structure is 3? statically indeterminate and so we might expect the number of plastic hinges required to be 4. However, since one of the indeterminacies is horizontal restraint, removing it would not change the bending behavior of the beam.

Thus for a bending collapse only 2 indeterminacies apply and so it will only take 3 plastic hinges to cause collapse. So looking at the elastic BMD, we'll assume a collapse mechanism with the 3 plastic hinges at the peak moment locations: A, B, and C.

And so the applied load is in equilibrium with the free BMD of the collapse BMD.

2. Mechanism:

From the proposed  collapse mechanism it is apparent that the beam is a mechanism.

3. Yield:

From the collapse BMD it can be seen that now here is exceeded. PM Thus the solution meets the three conditions and so, by the Uniqueness Theorem, is the correct solution.

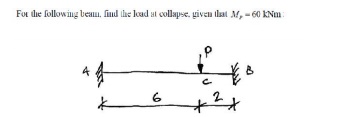
Example 3- Propped Cantilever with Two Point Loads

For the following beam, for a load factor of 2.0, find the required plastic moment capacity:

Once again we try to picture possible failure mechanisms. Since maximum moments occur underneath point loads, there are two real possibilities:

Therefore, we analyse both and apply the Upper bound Theorem to find the design plastic moment capacity.

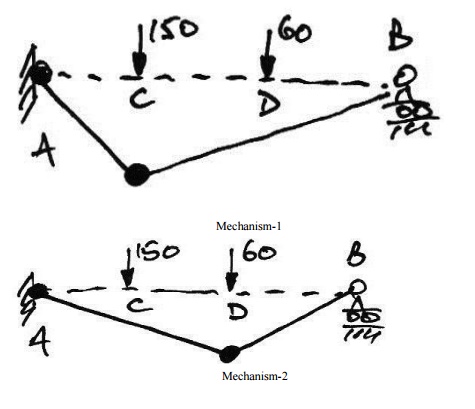
Mechanism1: Plastic Hingeat C:

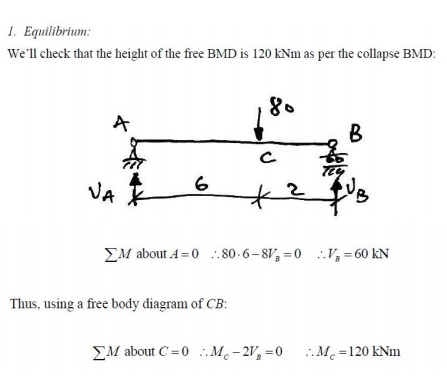
1. Equilibrium:

Using the BMD at collapse, we'll check that the height of the free BMD is that of the equivalents imply-supported beam. Firstly the collapse BMD from Mechanism1 is:

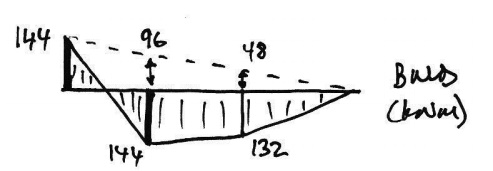
Hence, the total heights of the free BMD are:

Checking these using a simply-supported beam analysis

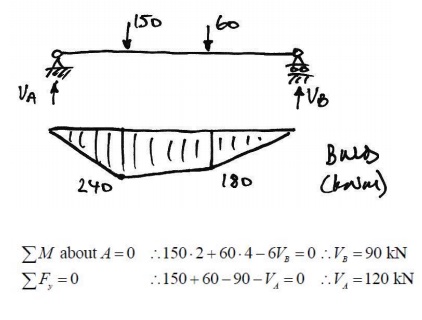
Thus, using appropriate free body diagrams of AC and DB:

And so the applied load is in equilibrium with the free BMD of the collapse BMD.

2. Mechanism:

From the proposed collapse mechanism it is apparent that the beam is a mechanism. Also, since it is a propped cantilever and thus one degree indeterminate, we require two plastic hinges for collapse, and these we have

3.Yield:

From the collapse BMD it can be seen that no where is the design exceeded. 144kNm Thus by the Uniqueness Theorem we have the correct solution. Lastly, we'll examine why the Mechanism 2 collapse is not the correct solution. Since the virtual work method provides an upper bound, then, by the Uniqueness Theorem, it must not be the correct solution because it must violate the yield condition. Using the collapse Mechanism 2 to determine reactions, we can draw the following BMD for collapse Mechanism 2:

From this it is apparent that Mechanism 2 is not the unique solution, and so the design plastic moment capacity must be 144 kNmasimplied previously from the Upper bound Theorem.

4.Basic Collapse Mechanisms:

In frames, the basic mechanisms of collapse are:

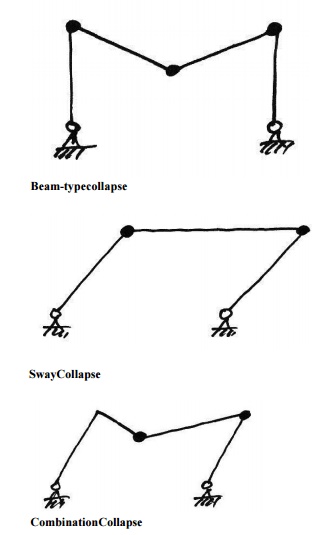
5. Combination of Mechanisms

One of the most powerful tools in plastic analysis is Combination of Mechanisms. This allows us to work out the virtual work equations for the beamandsway collapses separately and then combine them to find the collapse load factor for a combination collapse mechanism.

Combination of mechanisms is based  on the idea that  there are only a certain  number of independent equilibrium equations for a structure. Any further equations are obtained from a combination of these independent equations. Since equilibrium equations can be obtained using

virtual work applied to a possible collapse mechanism, it follows that there are independent collapse mechanisms, andother collapse mechanisms that may be obtained form a combination of the independent collapse mechanisms.

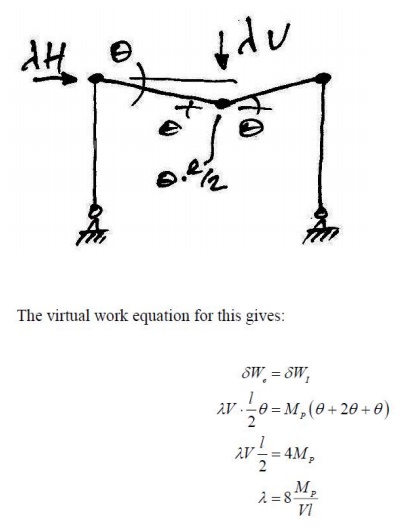
6. Simple Portal Frame

In this example we will consider a basic prismatic (so all members have the same plastic moment capacity) rectangular portal frame with pinned feet:

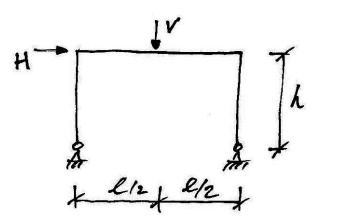
We will consider this general cases  othatwecaninferthe properties and behavior of all such frames. We will consider each of the possible mechanisms outlined above.

7.Beam collapse:

The possible beam collapse looks as follows: