Chapter: Civil : Structural Analysis : Plastic Analysis Of Structures
Beams in pure bending
Beams in pure bending
1. Material Behavior
Auniaxial tensile stress on a ductile material such as mild steel typically provides the following graph of stress versus strain:
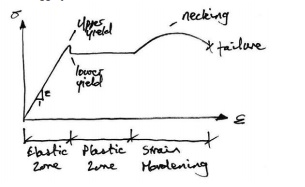
As can be seen, the material can sustain strains farinexcess of the strain at which yield occurs before failure. This property of the material is called its ductility. Though complex models do exist to accurately reflect the above real behavior of the material, the most common, and simplest, model is the idealized stress-strain curve. This is the curve for an ideal elastic-plastic material (which doesn't exist), and the graph is:
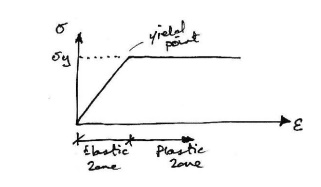
As can be seen, once the yield has been reached it is taken that an indefinite amount of strain can occur. Since so much post-yield strain is modeled, the actual material (or cross section) must also be capable of allowing such strains. That is, it must be sufficiently ductile for the idealized stress-strain curve to bevalid. Next we consider the behavior of across section of an ideal elastic-plastic material subject to bending. In doing so, we seek the relationship between applied moment and the rotation (or more accurately, the curvature) of across section.
2. Moment-Rotation Characteristics of General Cross Section
We consider an arbitrary cross-section with a vertical plane of symmetry, which is also the plane of loading. We consider the cross section subject to an increasing bending moment, and assess the stresses at each stage.
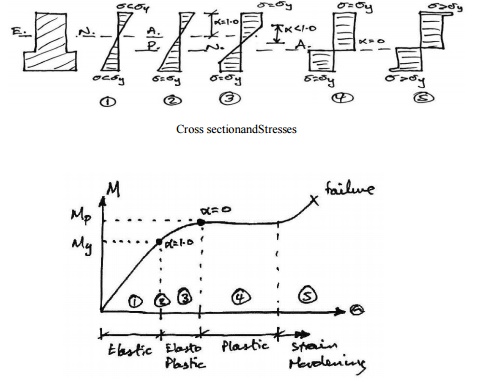
Stage1- Elastic Behaviour
The applied moment causes stresses over the cross-section that are all less than the yield stress of the material.
Stage2-Yield Moment
The applied moment is just sufficient that the yield stress of the material is reached at the outer most fibre(s) of the cross-section. All other stresses in the cross section are less than the yield stress. This is limit of applicability of an elastic analysis and of elastic design. Since all fibres are elastic, the ratio of the depth of the elastic to plastic regions,
Stage3- Elasto-Plastic Bending
The moment applied to the cross section has been increased beyond the yield moment. Since by the idealized stress-strain curve the material cannot sustain a stress greater than yield stress, the fibres at the yield stress have progressed inwards towards the centre of the beam. Thus over the cross section the reisanelastic core and a plastic region. The ratio of the depth of the elastic core to the plastic region is .
Since extra moment is being applied and no stress is bigger than the yield stress, extra rotation of the section occurs: the moment-rotation curve losses its linearity and curves, giving more rotation per unit moment (i.e. looses stiffness).
Stage4- Plastic Bending
The applied moment to the cross section is such that all fibres in the cross section are at yield stress. This is termed the Plastic Moment Capacity of the section since there are no fibres at an elastic stress, Also note that the full plastic moment requires an infinite strain at the neutral axis
And so is physically impossible to achieve. However, it is closely approximated in practice. Any attempt at increasing the moment at this points imply results in more rotation, once the cross-section has sufficient ductility. There fore in steel members the cross section classification must be plastic and in concrete members the section must be under-reinforced.
Stage5-Strain Hardening
Due to strain hardening of the material, a small amount of extra moment can be sustained.
The above moment-rotation curve represents the behavior of across section of a regular elastic-plastic material. However, it is usually further simplified as follows:
With this idealized moment-rotation curve, the cross section linearly sustains moment up to the plastic moment capacity of the section and then yields in rotation an indeterminate amount. Again, to use this idealization, the actual section must be capable of sustaining large rotations- that is it must be ductile.
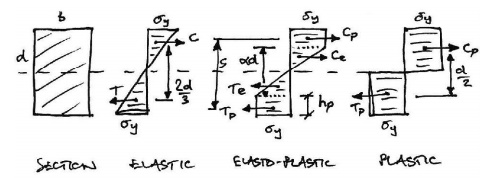
Analysis of Rectangular Cross Section
Since we now know that across section can sustain more load than just the yield moment, we are interested in how much more. In other words we want to find the yield moment and plastic moment, and we do so for a rectangular section. Taking the stress diagrams from those of the moment-rotation curve examined previously, we have:
Related Topics