Plane Curves and Introduction to Orthographic

PLANE CURVES AND INTRODUCTION TO ORTHOGRAPHIC

PROJECTION (Curves used in Engineering Practices)

Construction of Ellipse, parabola and hyperbola by eccentricity method only.

Construction of CYCLOID, INVOLUTE OF SQUARE AND CIRCLE only. Drawing normal and tangent to the above curves.

INTRODUCTION TO ORTHOGRAPHIC PROJECTION

Principle of 1st angle and 3rd angle projection. Projection of points situated in all the four quadrants. Problems involving projection of points, projection of two points situated indifferent quadrants.

Engineering Curves

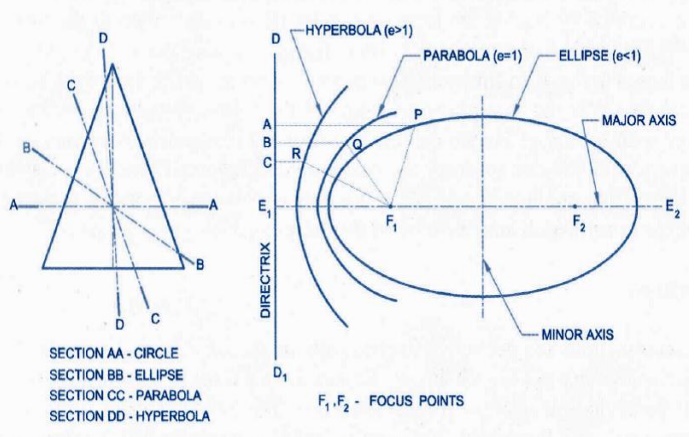
Construct an ellipse by eccentricity

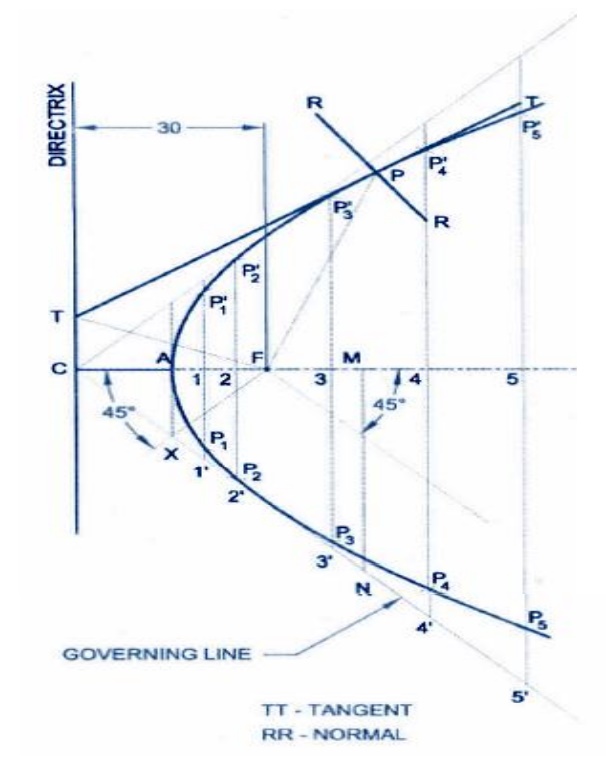
Construct a parabola by eccentricity

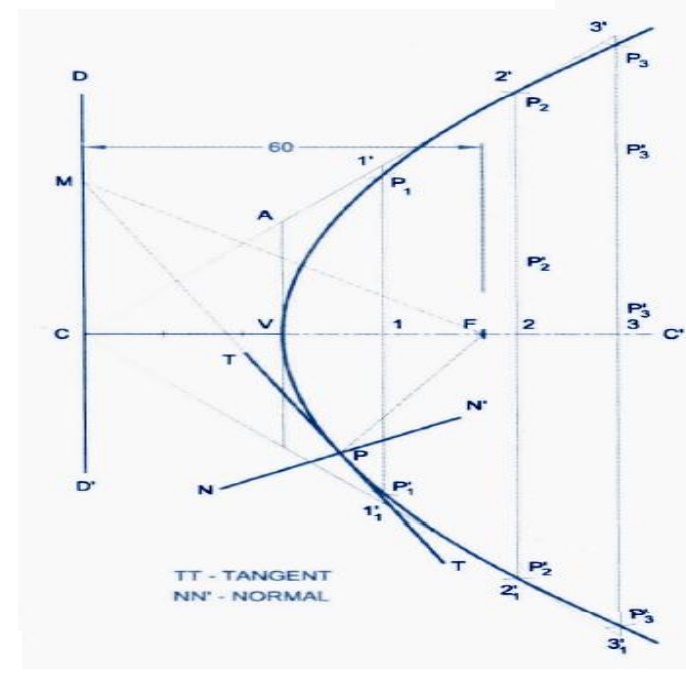
Construct a hyperbola by eccentricity

SPECIAL CURVES

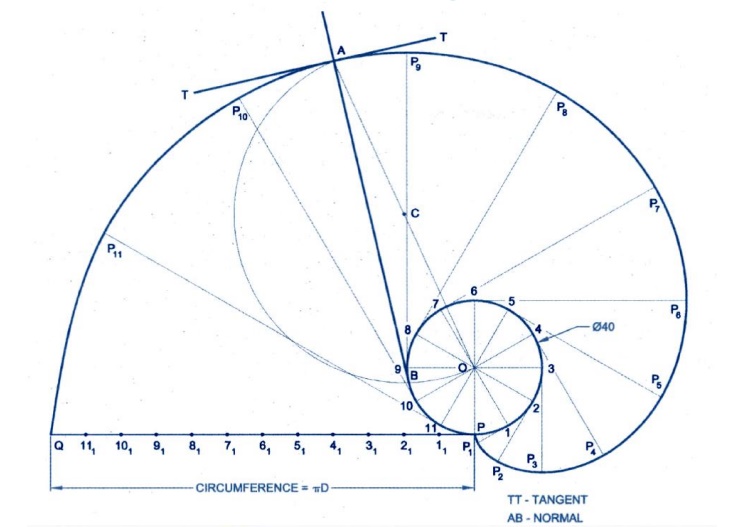
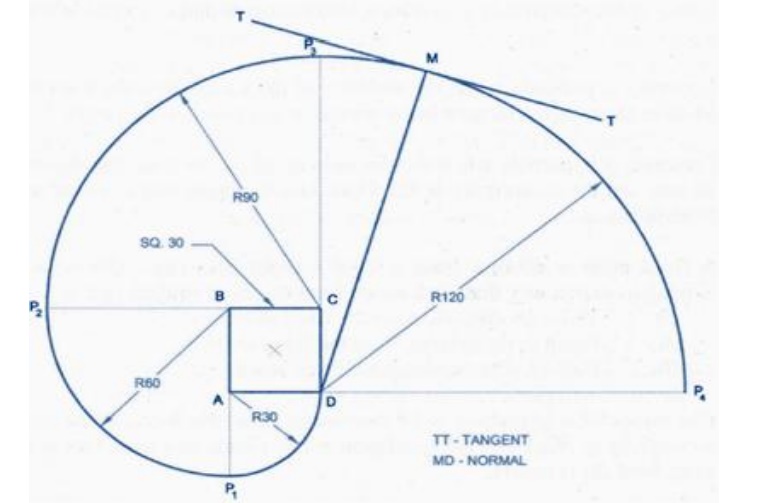
INVOLUTE:

An involute is the locus of a point on a string, as the string unwinds itself from a line or polygon, or a circle, keeping always the string taut.

INVOLUTE OF A CIRCLE AND SQUARE

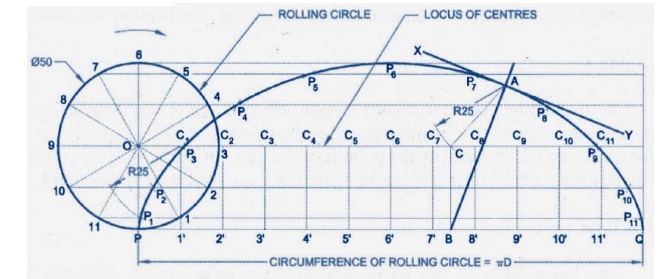
CYCLOIDAL:

Cycloid curves are formed by a point on the circumstance of a circle, rolling upon a line or an another circle. The rolling circle is called the generating circle. The line on which the generating circle rolls is called base line. The circle on which the generating circle rolls is called directing or base circle. A cycloid is a curve traced by a point on the circumference of a circle which rolls without slipping along a line

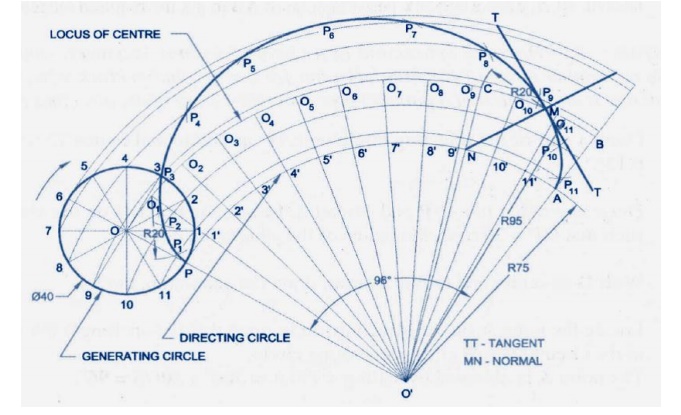
EPICYCLOID:

An epicycloids is a curve traced by a point on the circumference of a circle which Rolls without slipping on the outside of an another circle.

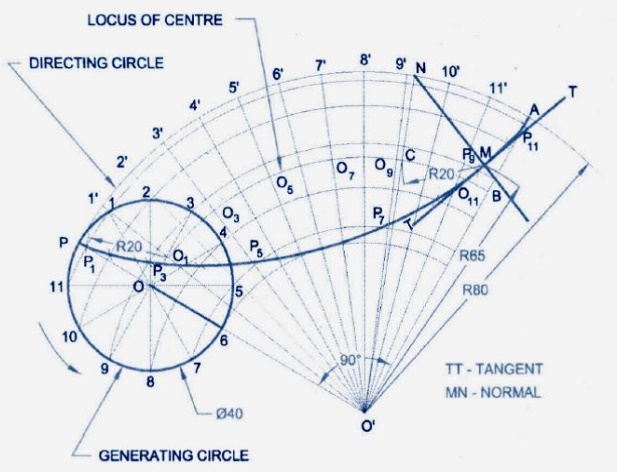
HYPOCYCLOID:

A hypocycloid is a curve traced by a point on the circumference of a circle when it rolls without slipping on the inside of another circle.

Projection of Points:

A point is simply a space location of infinitesimal size. It may represent the corner of an object, the intersection of two lines or a designated spot in space. The projection obtained on vertical plane VP is called the elevation and on horizontal plane HP, the plan. The intersection line of the vertical plane and the horizontal plane is known as ground line or reference line.

Position of points:

(i)                   In front of the VP and above the HP

(ii)                In front of the VP and in the HP

(iii)              In the VP and above the HP

(iv)              Behind the VP and above the HP

(v)                Behind the VP and in the HP

(vi)              Behind the VP and below the HP

(vii)           In the VP and below the HP

(viii)            In front of the VP and below the HP

(ix)                In the VP and HP

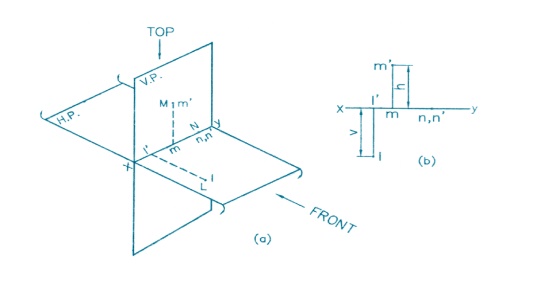
GENERAL PROCEDURE TO DRAW PROJECTION OF POINTS

1.     From given data identify the quadrant

2.     Draw the XY line and projection

3.     Along this projector mark by dots the distances of the given point form the HP and VP, on the corresponding side of the XY line, depending upon the quadrant in which the point lies, to locate the front view and the top view, respectively.

4.     Make the front view and the top view bold and rub off the unwanted length of the projector to complete the solution.

Important Questions

1.   Draw the involutes of a circle of diameter 40mm and draw the tangent and

the normal to the involutes   at any points on the curve.

2.        Draw the front, top, and side views of the object shown below.

3.        Draw the coin cure, if the distance of focus from the directory is 70mm and the eccentricity is ¾. Also draw a tangent and a normal at any point on the curve.

4.        A circle of 50mm diameter rolls as a horizontal line for ¾ of a revolution clockwise. Draw the path traced by point P on the circumference of the circle. Also draw a tangent and normal at any point on the cure

5.        Draw a hyperbola when the distance between its focus and directrix is 50mm and eccentricity is 3/2. Also draw the tangent and normal at a point 23mm from the directrix.

6.        The focus of a conic is 50mm front the directory. Draw the locus of a point P moving in such a way that its distance from the directrix is equal to its distance from the focus. Name the cure. Draw a tangent to the curve at a point 60mm from the directrix.

7.        Draw the involutes of a circle of diameter 40mm and draw the tangent and the normal to the involutes at any point on the cure.