Development of Surfaces and Isometric Projection

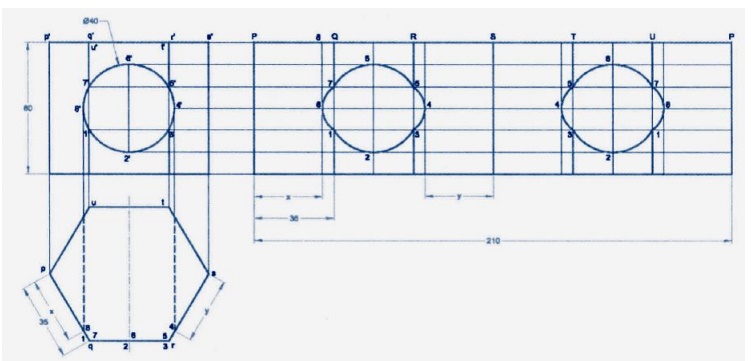
DEVELOPMENT OF SURFACES AND ISOMETRIC PROJECTION

Development of lateral surfaces of vertical prism, cylinder pyramid, and cone truncated by surfaces of inclined to HP alone. Development of surfaces of vertical cylinder and prism with cylindrical cut outs perpendicular to the axis. Isometric projection of solids like prism, pyramid, cylinder and cone; combination of any two; truncation when solid is in simple vertical position, by a cutting plane inclined to HP.

Development of surfaces:

A layout of the complete surface of a three dimensional object on a plane surface is called its development or pattern. Development is a term frequently used in sheet metal work where it means the unfolding or unrolling of a detail into a flat sheet called a pattern

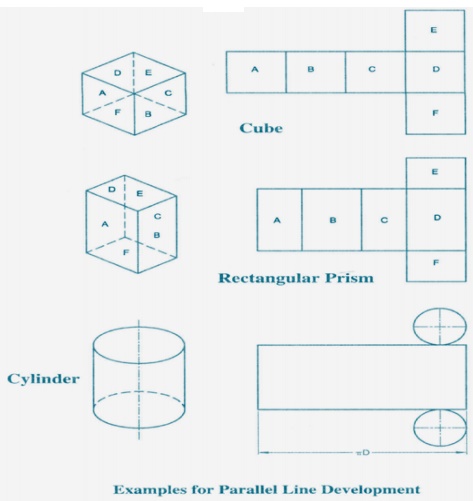
There are three methods of pattern development; (i) Parallel line, (ii) Radial line and (iii) Triangulation.

Parallel Line Method:

This method can only be used to develop objects (or parts thereof) having a constant cross-section for their full length, for example, prisms and cylinders and related forms. Parallel lines, parallel to the axis of the detail, are shown on a view which shows them as their true lengths.

1. After drawing the given views, determine the view in which the right section of the solid appears as an edge view. Here it should be noted that top views of right prisms and cylinders are equivalent to their right sections will have to be found

in the form of an auxiliary view.

2.       Layout the stretch-out line of the development parallel to the edge view of the right section.

3.          Locate the distance between lateral comer edges by measuring from the true size views in the right section and then transferring these measurements to the stretch-out line. Name their points.

4.      Draw the lateral fold lines perpendicular to the stretch-out line through the points already plotted.

5.     The development should be commenced at the shortest line, so that the least amount of welding or other joining effort is required.

6.       Join all end points forming the boundary of the pattern in proper order. Only the boundary of the pattern should be made bold, leaving all other lines as thin lines.

7.      Check up that the point where the development ends is the same point as the beginning point on the right section.

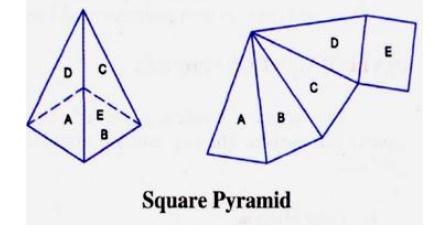
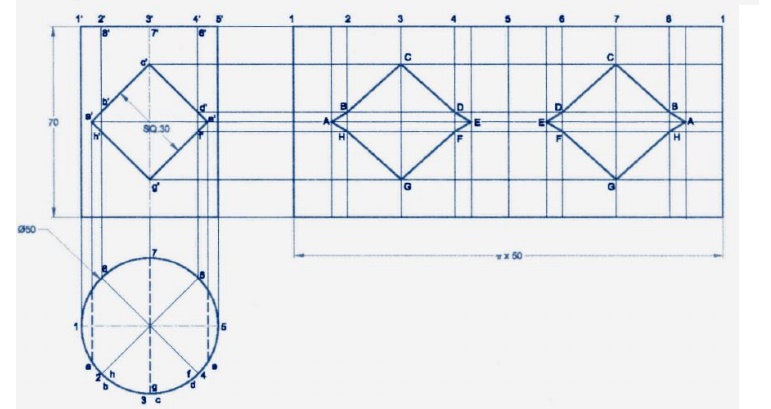
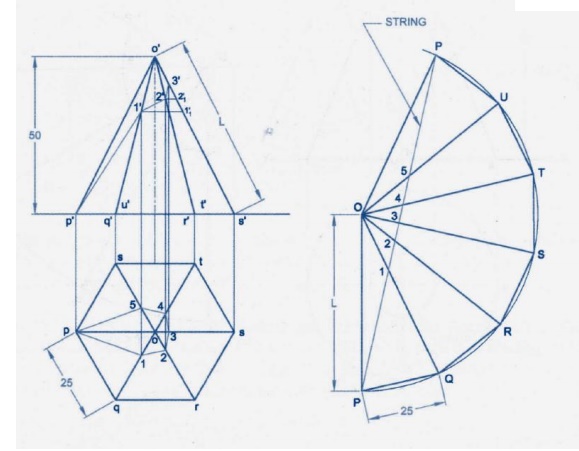
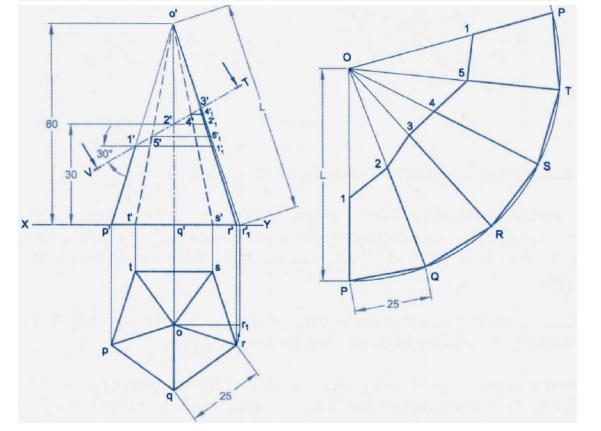
Radial Line Method:

This method of development is used for right and oblique pyramids and cones. It employs radial lines which are slant edges from vertex to base comer points for pyramids, and radial surface lines on the cone surface from the vertex to the base.

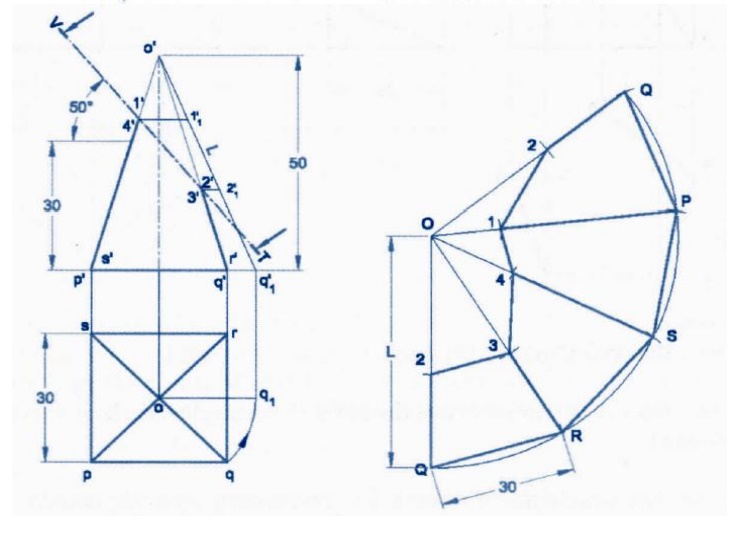
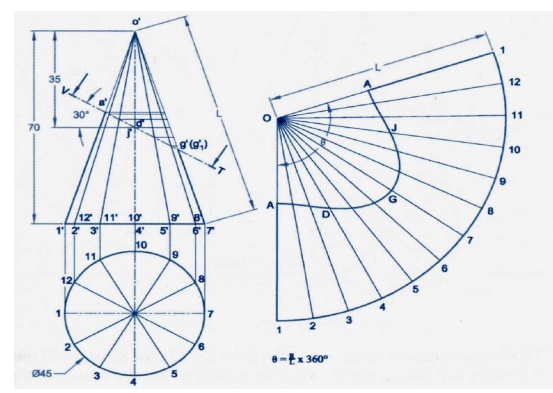
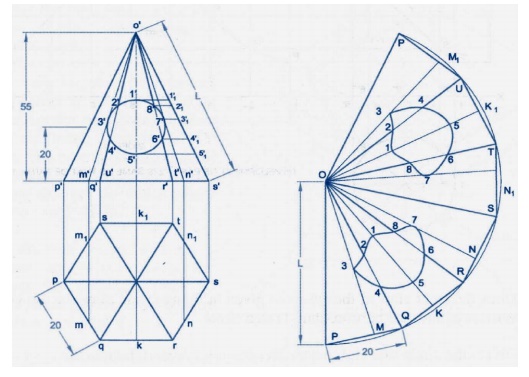
Development of Right Cones

The development of any right cone is a sector of a circle since the radial surface Lines are all of the same true length. The angle at centre of the sector depends on the base radius and the slant height of the cone. Let the radius of the base of the cone be R, the slant height of the cone be L, and the angle at the centre of the development be θ.

θ = (Radius of the base circle /True slant length) X 360 =( R / L ) X 360

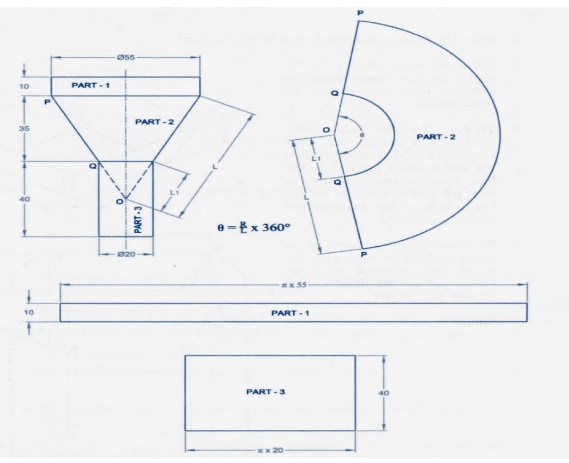
In this method of development the surface of the object is divided into a number of triangles. The true sizes of the triangles are found and then these triangles are drawn in order, side by side, to produce the pattern. It is simple to realize that to find the true sizes of the triangles, it is first necessary to find the true length of their sides.

1.      When the top and bottom edges of a sheet metal detail are parallel to the HP the true lengths of these edges may be taken directly from the top view.

2.       In case of circular edges, chordal distance may be taken and transferred to the development. Though such lengths are not theoretically accurate they are satisfactory for development work.

3.        For all transition pieces having inclined top and bottom edges, TL construction must be carried out if these edges are curved.

4.      A well defined labeling system should be used in order that the construction technique may be progressive and easy to understand.

Isometric Projection:

The isomeric projection of an object is obtained on a vertical plane of projection by placing the object in such a way that its three mutually perpendicular edges make equal inclinations with the plane of projection. Since the three mutually perpendicular edges of an object are projected in the isometric projection at equal axonometric angles, the angles between those edges in the isometric projection will be at 12°. The lengths of the three mutually perpendicular edges of the object in the isometric projection are foreshortened in the same proportion.

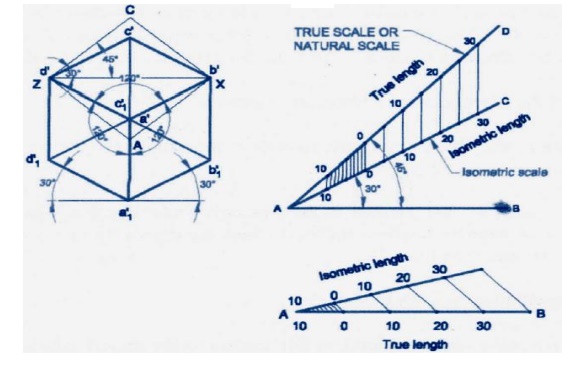
Isometric Scale:

In the isometric projection, all the edges of an object along the direction of the three isometric axes are foreshortened to 0.816 times their actual lengths. To facilitate an easy and quick method of measurement of the lengths of the different edges in their reduced sizes while drawing the isometric projection of the object, a special scale called isometric scale is constructed.

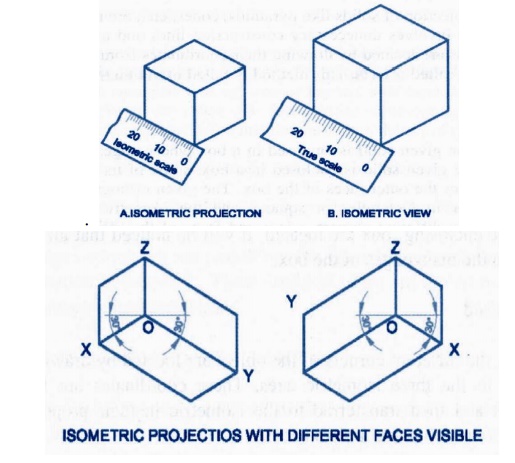
The view drawn to the actual scale is called the isometric view or Isometric Drawing while that drawn using the isometric scale is called the Isometric Projection.

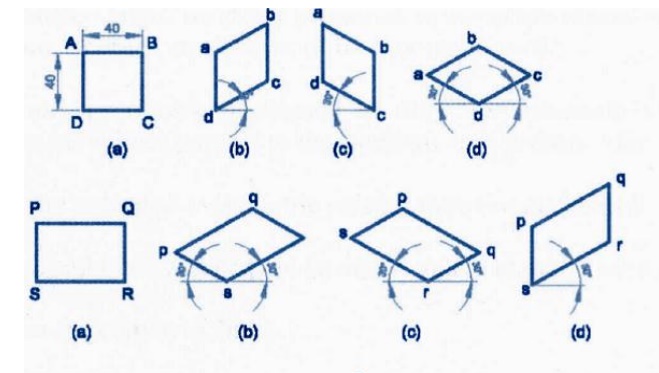
Importance Points in Isometric:

1.           For drawing the isometric, the object must be viewed such that either the front -right or the left edges becomes nearest.

2.              All vertical edges of the object remain vertical in isometric

The horizontal edges of the object which are parallel to the isometric axes are drawn at 30° to the horizontal.

4.     The inclined edges which are not parallel to the isometric axes should not be drawn at the given inclination in isometric. These inclined edges are drawn by first locating the end points in isometric and then joined.

5.     All circles are represented as ellipses in isometric.

6.     All construction lines have to be retained as thin lines and the visible edges are to be shown as thick lines.

7.     Generally the hidden edges need not be shown in isometric unless otherwise required either for locating a comer, or an edge, or face, or mentioned.

8.     Unless otherwise specifically mentioned to draw the isometric view or isometric drawing all dimension lines parallel to the isometric unless otherwise if mentioned.

9.     No dimensions are indicated in isometric unless otherwise mentioned.

The given orthographic views need not be drawn unless required for consideration

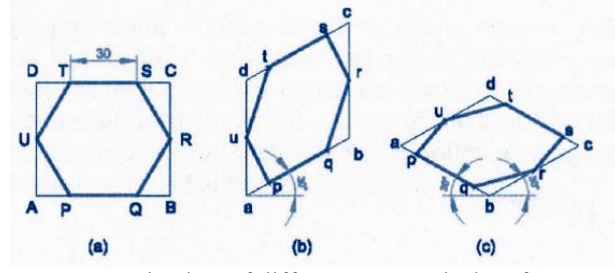
Isometric view of different geometrical surfaces

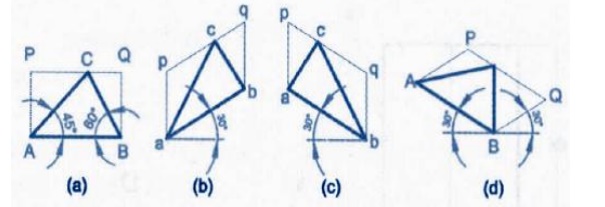
Isometric view of triangle

Isometric view of semi circle

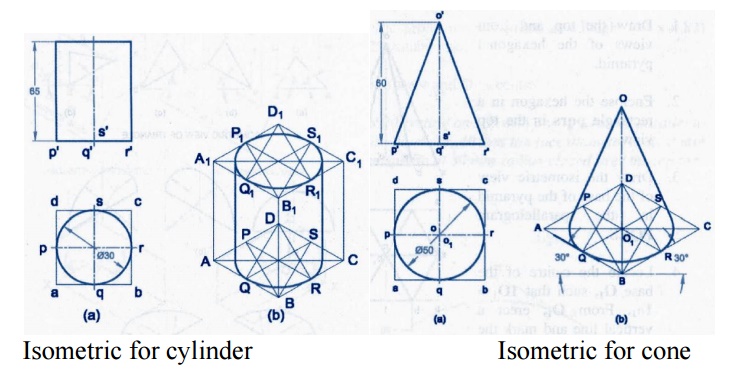
Isometric for cylinder                                                    Isometric for cone

Isometric for prism                                              Isometric for pyramid

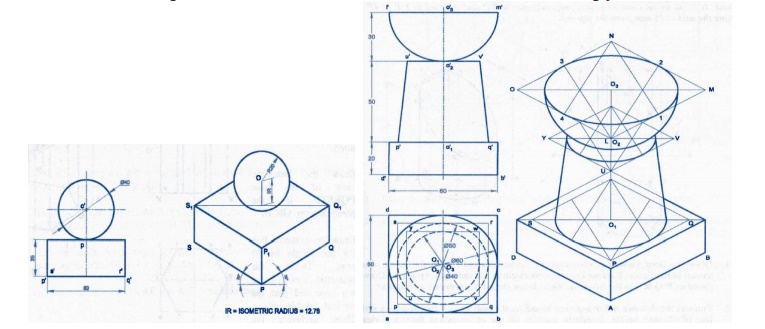
Isometric for combination solid

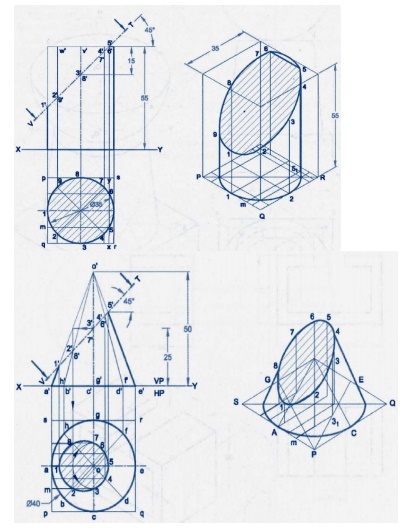
Isometric for cutting model in cylinder and cone

Isometric for cutting model in cone and pyramid

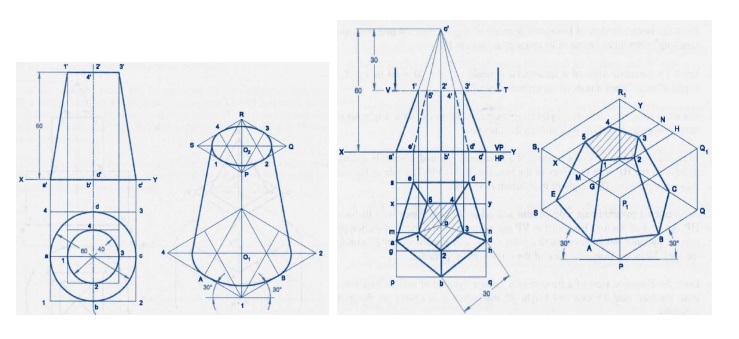
Isometric for cutting model square pyramid

Important Questions

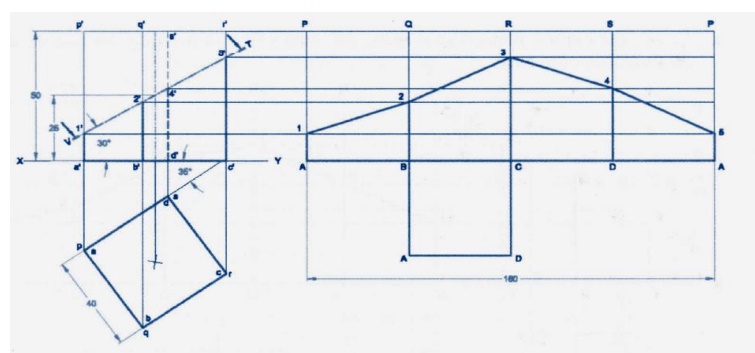
1.         A cylinder of diameter 40mm and height50mm is resting vertically on one of its end on the hp. It is cut by a plane perpendicular to the vp and inclined at 30®to the hp. The plane meets the axis at a point 30mm from the base. Draw the development of the lateral surface of the lower portions of the truncated cylinder.

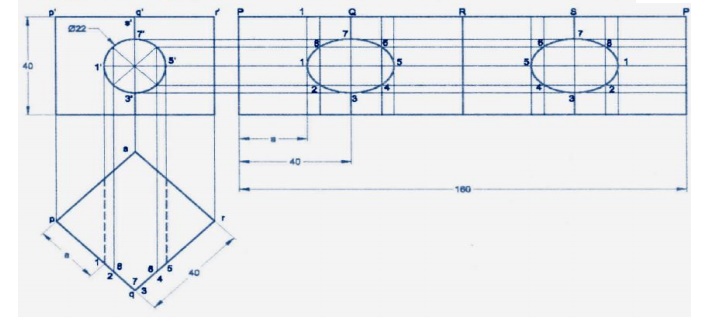
2.         A hexagonal prism of base side 20mm and height 40mm has a square hole of side 16mm at the centre. The axes of the square and hexagon coincide. One of the faces of the square is parallel to the face of the hexagon. Draw the isometric projection of the prism with hole to full scale.

3.   A right circular cone, 40mm base and 50mm height, rests on its base on HP. A section plane perpendicular to VP and inclined to HP AT 45®cuts the cone bisecting axis. Draw projections of the truncated cone and develop its lateral surface.

4.         A pentagonal pyramid of 40mm edge of base and height 70mm rests with its base on HP. One of the bases edges is perpendicular to VP and line on the left of axis of the pyramid. A section plane perpendicular to VP and inclined at 30®to VP cut the axis of the pyramid at a point 30mm above the base of the pyramid. Draw the isometric projection of the truncated pyramid.

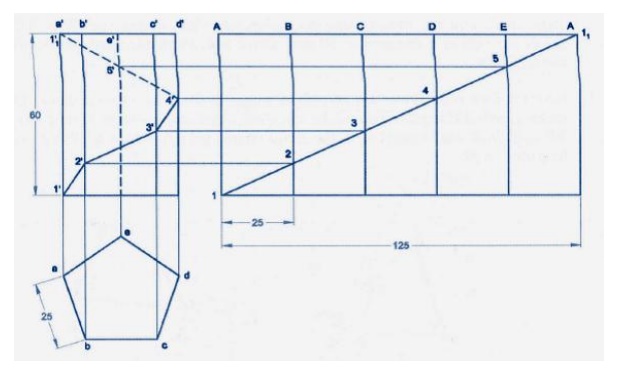
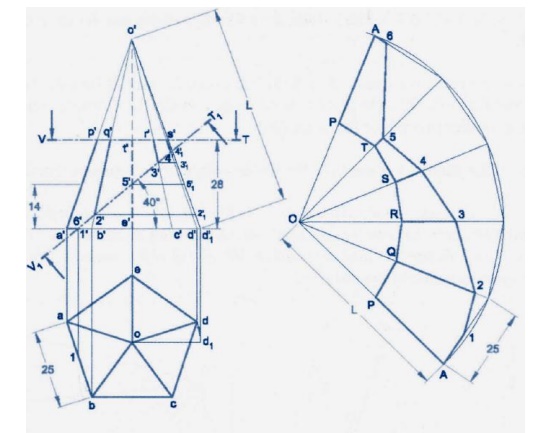
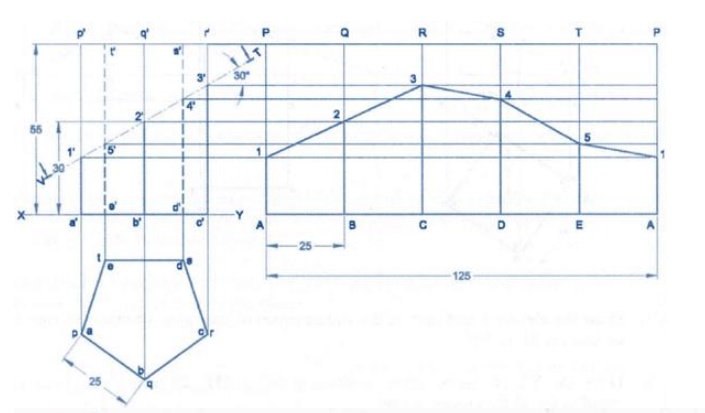
5.         A pentagonal pyramid of base edge 25mm and height 60mm rests vertically on its base on the HP such that one of its base edge parallel to VP. It is cut by a plane, inclined at 60 to HP and passes through a point 35mm from the apex. Draw the development of the lateral surface of the pyramid.

6.         An object consists of a hemispherical vessel of 80mm diameter which is placed    centrally over a cylinder of 50mm diameter and height of 60mm. the cylinder in turn is placed centrally over a square prism of 60mm base side and 20mmh height. Draw the isometric projection of the object.

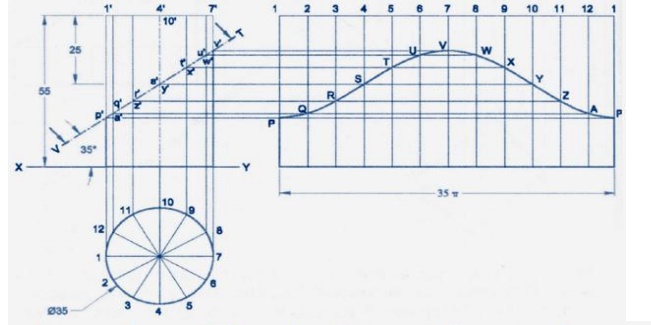
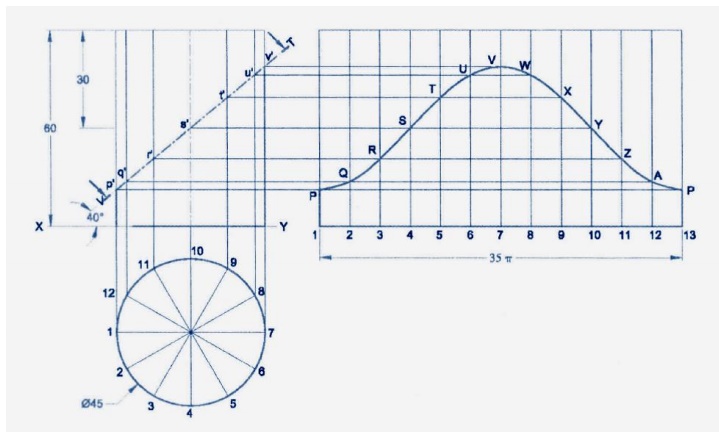
7.        Draw the development of the lateral surface of the lower portion of a cylinder of diameter 50mm and axis 70mm. the solid is cut by a sectional plane inclined at 40®to HP and perpendicular to VP and passing through the midpoint of the axis.

8.        Draw the isometric projection of the object from the view shown in figure.

9.        A regular hexagonal pyramid side of base 20mm and height 60mm is resting vertically on its base on HP, such that two of the sides of the base are perpendicular the VP. It is cut by a plane inclined at 40® to HP and

perpendicular to VP. The cutting plane bisects the axis of the pyramid. Obtain the development of the lateral surface of the truncated pyramid.

10.      A cylinder of 50mm diameter and 75mm height stands with its base on HP. It is cut by a section plane inclined at 45® to HP and perpendicular to VP passing through a point on the axis 20mm below the top end. Draw the isometric projection at the truncated cylinder.

11.      A cylinder of diameter 40mm and height 50mm is resting vertically on one of its ends on the HP. It is cut by a plane perpendicular to the VP and inclined at 30® to the HP. The plane meets the axis at a point 30mm from the base. Draw the development of the lateral surface of the lower portion of the truncated cylinder.

12.      A hexagonal prism of base side 20mm and height 40mm has a square hole of side 16mm at center. The axis of the square and hexagon coincide. One of the faces of the square hole is parallel to the face of the hexagon. Draw the isometric projection of the prism with hole of full scale.