Definition, Formula, Properties, Solved Example Problems, Exercise | Mathematics - Permutations | 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Chapter: 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Permutations
Permutations
What is a permutation ?
Permuations come in various
disguises.
Suppose three friends A, B and C
have to stand in line for a photograph. In how many order can they stand? Some
of the possible arrangements (from left to right) are
A, B, C: A, C, B: B, A, C
B, C, A: C, B, A: C, A, B.
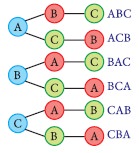
Thus there are six
possible ways in which they can arrange themselves for the photograph.
Thus if 3 objects have
to be arranged in a row there are 3 × 2 × 1 = 3! possible
permutations. The number of permutations of 4 objects taken all at a time is 4 × 3 × 2 × 1 = 4! Thus if n objects have to be arranged in a line there are n × (n
− 1) × (n − 2) × · · · × 3 × 2 × 1 = n! possible arrangements or permutations.
Suppose you have 7
letters A,B,C,D,E,F and G. We want to make a 4 letter string. We have 7 choices
for the 1st letter. Having chosen the first letter, we have 6 choices for the
second letter. Proceeding this way, we have 4 choices for the 4th letter.
Hence, the number of
permutations of 4 letters chosen from 7 letters is

1. Permutations of distinct objects
In terms of function
on any finite set say S = {x1, x2, ...xn}, a permutation can be
defined as a bijective mapping on the set S onto itself. The
number of permutation on the set S is the same as the
total number of bijective mappings on the set S.
We denote the number
of permutations by nPr.
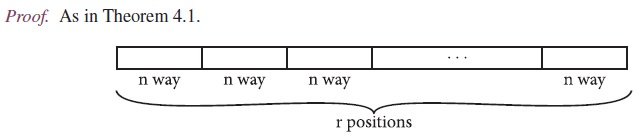
Theorem 4.1: If n, r are positive integers and r ≤ n, then the number of
permutations of
n distinct
objects taken r at a time is n (n
− 1)
(n − 2) · · · (n
− r + 1).
Proof. A permutation is an
ordering. A permutation of n distinct objects taken r at a time is formed by filling of r positions, in a row
with objects chosen from the given n distinct objects.

There are n objects that can be filled in the first position. For the
second position there are remaining n − 1 objects. There are n − 2 objects for the third position. Continuing
like this until finally we place one of the (n − (r − 1)) possible objects in the rth position. By the rule of product we conclude nPr = n (n
− 1)
(n − 2) · · · (n
− r + 1).

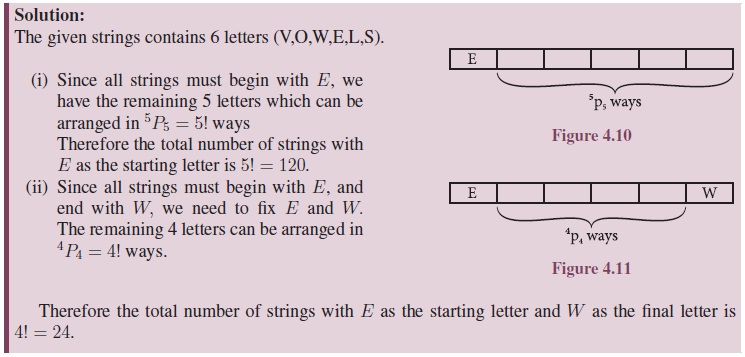
Theorem 4.3: The number of permutations of n different objects taken r at a time where repetition is allowed, is nr.
We can fill the first position with n objects. For the second position (still we can use the object used in first position), there are n objects, and so on the rth position can be filled with n objects.By the rule of product, The number of permutations of n different objects taken r at a time when repetition allowed is n × n × n × · · · n (r times) = nr.
2. Properties of Permutations





3. Objects always together (String method)
The number of permutations of n different objects, taken all at
a time, when m specified objects are always
together,
·
Consider a string of m specified objects as
a single unit
·
Then we have (n − m + 1) objects. Permute this (n
− m + 1) objects in (n − m + 1)! ways.
·
Then permute the m specified objects
between themselves in m! ways.
·
Finally, the answer is m! × (n
− m + 1)!.
4. No two things are together (Gap method)
To obtain the number of
permutations of n different objects when no two of
k given objects occur together and there are no restrictions on
the remaining m = n − k objects, we follow the procedure
as follows:
·
First of all, arrange the m objects on which
there is no restriction in a row. These m objects can be permuted in mPm = m! ways.
·
Then count the number of gaps between every two of m objects on which there is no restriction including the end
positions. Number of such gaps will be one more than m that is (m + 1). In this m + 1 gaps,
we can permute the k objects in m+1Pk ways.
·
Then the required number of ways are m! ×(m+1) Pk.




To understand the next
problem we now define, The Rank of a word in the
dictionary.
It is the place at
which the given word comes when writing all the strings formed by the letters
of the given word in the dictionary order or lexicographic order.

5. Permutations of not all distinct objects
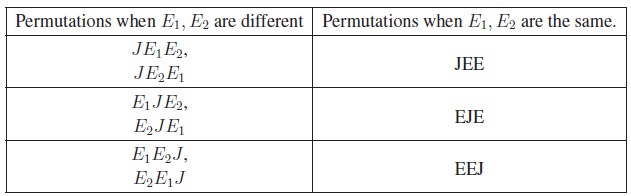
Consider permuting the
letters of the word JEE. In this case the letters of the word are not different.
There are 2 E’s, which are of same kind. Let us treat, temporarily, the 2 E’s
as different, say E1 and E2. The number of
permutations of 3 different letters taken all at a time is 3!.


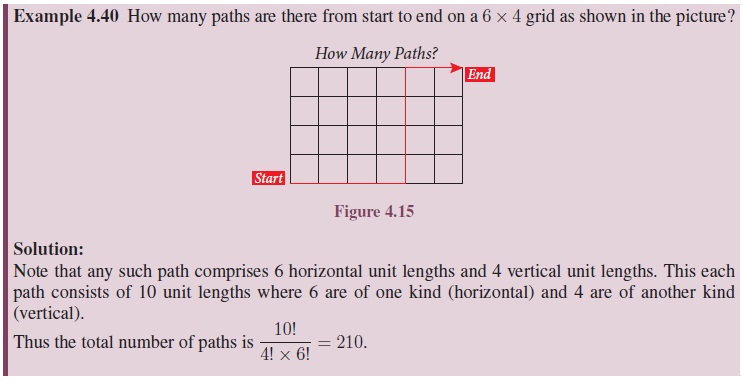





Related Topics