Definition, Solved Example Problems, Exercise | Mathematics - Mathematical induction | 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Chapter: 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Mathematical induction
Mathematical
induction
Let us consider the
sum of the first n positive odd numbers. These are 1,
3,
5,
7,
· · · , 2n
− 1. The first odd number
1 which is equal to 1. The first two odd numbers are 1 and 3 and their sum is 4. Writing these as follows helps us to see a pattern.
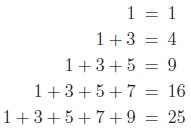
and so on. We note
that the right hand side of the expressions are the perfect squares 1,
4,
9,
16,
25 · · · . This pattern
compels us to make the conjecture that the sum of the first n odd numbers is equal to n2. Symbolically, we
express this as,
1 + 3 + 5 + · · · + (2n − 1) = n2.
However we have only
made a conjecture. In order to prove the conjecture we shall use the Principle
of Mathematical Induction. Mathematical Induction is a method or technique of
proving mathematical results or theorems of the above kind. This technique
relies upon making conjectures by observing all possible cases of a specific
result. It is well suited for proving results in algebra or in other
disciplines of mathematics where results or theorems are stated in terms of n, n being a positive
integer. The process of Mathematical Induction may be compared to that of
climbing an infinite staircase.
In order to ensure
that we complete the climb, it is sufficient to ensure the following.
a.
We can climb the first step.
b.
Once we have reached a particular step of the staircase, we can
climb to the next step.
Being sure of (a) and
(b) will enable us to climb all the steps in the staircase. Similarly, when we
apply this method to prove a mathematical statement P (n),
the process of induction involves the following steps.


One of the interesting
method of proof in Mathematics is by the Mathematical induction. We shall
illustrate the method through problems. As an illustration of the process let
us revisit a well known result through an example below:










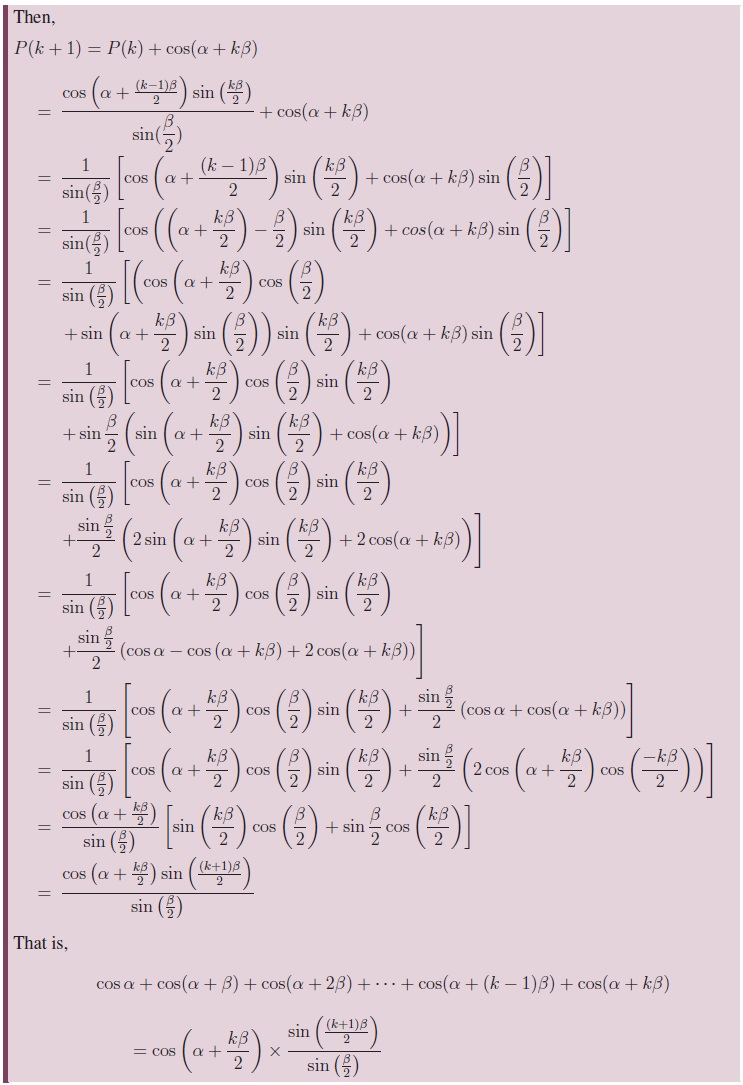




Related Topics