Definition, Formula, Solved Example Problems, Exercise | Mathematics - Combinations | 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Chapter: 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Combinations
Combinations
Let us suppose there
are four persons A, B, C and D (actual names may be used here) and we have to select three of
them to be a part of a committee. In how many ways can we make this selection?
For example, A, B, C is one possible
choice. Here the order of selection is immaterial. Thus A, B, C is the same as B, A, C or C, A, B as long as the same three persons are selected. Thus the
possible distinct choices or selections are A, B, C; A, B, D; A, C, D and B, C, D. We may thus conclude that there are 4 ways of selecting 3
people out of 4. Each choice or selection is referred to as a combination of 4
different objects taken 3 at a time.
Suppose two persons
are to be selected from four persons. The possible choices are: A, B : A, C: A, D : B, C : B, D : C, D. Thus the number of combinations of 4
different objects taken 2 at
a time is 6. The number of
combinations of n different objects
taken r at a time is represented by nCr. From the above we may conclude that 4C3 = 4 and 4C2 = 6. Now, 4C3 is the number of combinations
of 4 objects taken 3 at a time. Note that in each combination, the three objects may
be arranged in 3! ways.
Thus the total number
of permutations of 4 objects taken 3 at a time is 4C3 × 3!. This is also equal
to 4P3. Hence 4P3 =4 C3 × 3!.
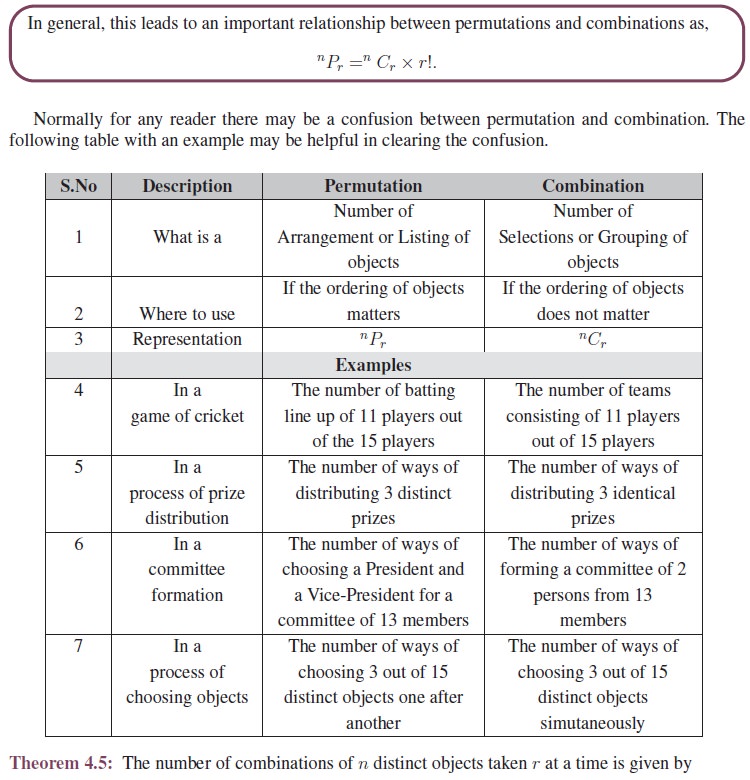

1. Properties of Combinations


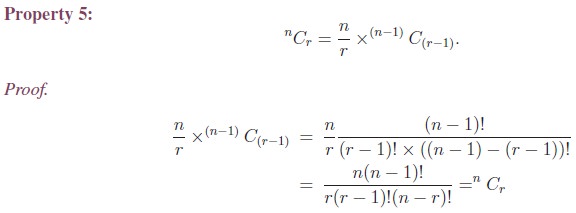












Related Topics