Fundamental principles of counting

Fundamental principles of counting

1. The Sum Rule:  Let us consider two tasks which need to be completed. If the first task can be completed in M different ways and the second in N different ways, and if these cannot be performed simultaneously, then there are M + N ways of doing either task. This is the sum rule of counting.

2. The Product Rule:  Let us suppose that a task comprises of two procedures. If the first procedure can be completed in M different ways and the second procedure can be done in N different ways after the first procedure is done, then the total number of ways of completing the task is M × N

3. The Inclusion-Exclusion Principle: Suppose two tasks A and B can be performed simultaneously. Let n(A) and n(B) represent the number of ways of performing the tasks A and B independent of each other. Also let n(A ∩ B) be the number of ways of performing the two tasks simultaneously. We cannot use the sum rule to count the number of ways of performing one of the tasks as that would lead to over counting. To obtain the correct number of ways we add the number of ways of performing each of the two tasks and then subtract the number of ways of doing both tasks simultaneously. This method is referred to as the principle of inclusion - exclusion. Using the notation of set theory we write it as

n(A ∪ B) = n(A) + n(B) − n(A ∩ B).

Suppose we have to find the number of positive integers divisible by 2 or 7 (but not both), upto 1000. Let n(A) denote the number of integers divisible by 2, n(B) denote the number of integers divisible by 7 and n(A ∩ B) the number of integers divisible by both 2 and 7. Then the number of positive integers divisible by 2 or 7 is given by

n(A ∪ B) = n(A) + n(B) − n(A ∩ B) = 500 + 142 − 71 = 571.

(Note that n(A) will include all multiples of 2 upto 1000, n(B) will include all multiples of 7 upto 1000 and so on.)

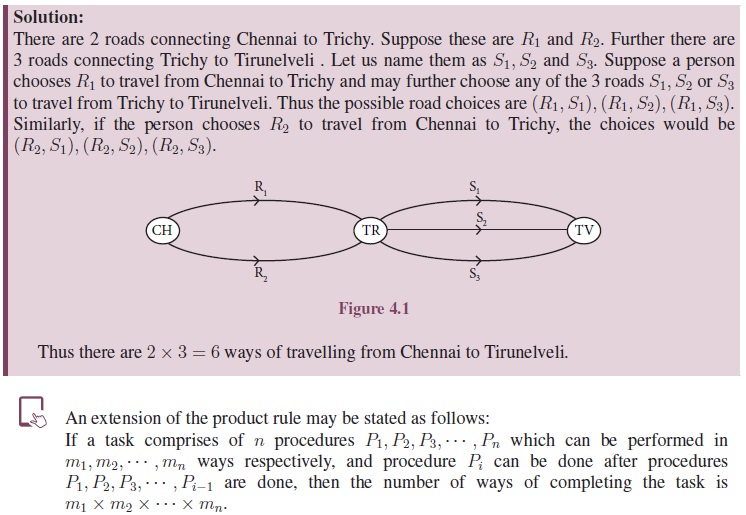
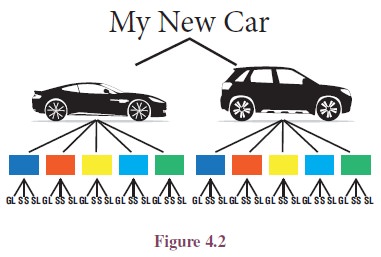
Tree Diagrams: Tree diagrams are often helpful in representing the possibilities in a counting problem. Typically in a tree the branches represent the various possibilities. For example, suppose a person wants to buy a Car for the family. There are two different branded cars and five colours are available for each brand. Each colour will have three different variant on it namely GL,SS,SL. Then the various choices for choosing a car can be represented through a tree diagram as follows:

Another concept which is an essential tool in a counting process which is stated as follows:

In order to understand the Permutation and Combinations we need a concept called “Factorials” which will be discussed in the next section.