Definition, Formula, Solved Example Problems, Exercise | Mathematics - Factorials | 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Chapter: 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Factorials
Factorials
Factorial of a natural number n
is the product of the first n natural numbers. It is denoted by n!.
That is,
n!=1 × 2 × 3 ×···× n.
We read this symbol as
“n factorial” or “factorial of n”. The notation n! was introduced by the
French mathematician Christian Kramp in the year 1808. Note that for a positive
integer n
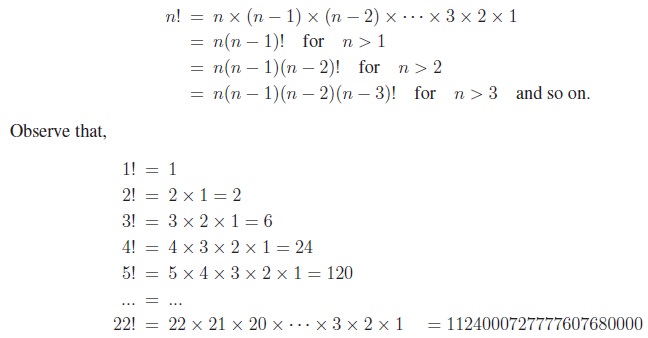
The number 22 ( the
Birth date of Ramanujan) has a special place with respect to factorial that, it
is the least integer N greater than 1 whose factorial has exactly N digits.
It will be a good
exercise for both students and teachers to find the next number N such that N! has exactly N digits.
Note that 0! = 1 is evident by
substituting n = 0 in the equation (n
+ 1)! = (n
+ 1) × n! as 1! = (0 + 1) × 0! ⇒ 0! = 1! / 1 = 1. This way, we talk of
factorial for non-negative integers. Note that factorials can be extended to certain negative numbers and
also to complex numbers, which are beyond the scope of this book.
We shall now discuss
certain examples in order to familiarise the computation of factorials.
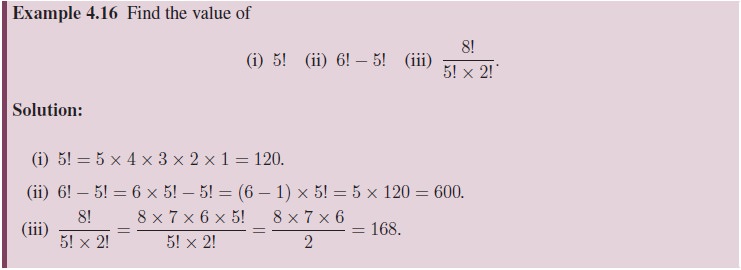






Related Topics