Combinatorics and Mathematical Induction | Mathematics - Exercise 4.5: Choose the correct or the most suitable answer | 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Chapter: 11th Mathematics : UNIT 4 : Combinatorics and Mathematical Induction
Exercise 4.5: Choose the correct or the most suitable answer
CHAPTER
: Combinatorics and Mathematical Induction
Choose the correct or the most suitable answer
1. The sum of the digits at the 10th
place of all numbers formed with the help of 2, 4, 5, 7 taken all at a time is
(1) 432
(2)
108
(3) 36
(4) 18
Solution

2. In an examination there are three
multiple choice questions and each question has 5 choices .
Number of ways in which a student can
fail to get all answer correct is
(1) 125
(2)
124
(3) 64
(4) 63
Solution

3. The number of ways in which the
following prize be given to a class of 30 boys first and second in mathematics,
first and second in physics, first in chemistry and first in English is
(1)
304 x 292
(2) 303 x 293
(3) 302 x 294
(4) 30 x 295.
Solution
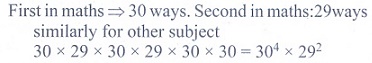
4. The number of 5 digit numbers all
digits of which are odd is
(1) 25
(2)
55
(3) 56
(4) 625.
Solution

5. In 3 fingers, the number of ways four
rings can be worn is ………..ways.
(1) 43 - 1
(2) 34
(3) 68
(4)
64
Solution
4 rings can be worn in 3 fingers in 34 ways
6. If (n+5)P(n+1)
= ( 11(n-1) /2 )(n+3)Pn,
then the value of n are
(1) 7 and 11
(2)
6 and 7
(3) 2 and 11
(4) 2 and 6.
Solution
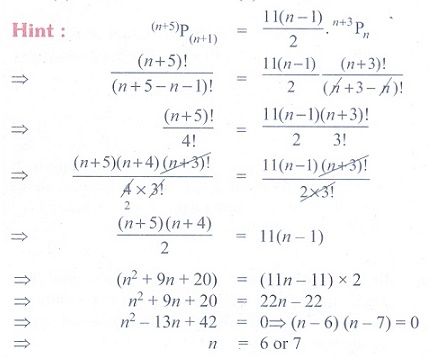
7. The product of r consecutive positive
integers is divisible by
(1)
r!
(2) (r - 1)!
(3) (r + 1)!
(4) rr.
Solution
Product of r consecutive positive integers is divisible by r! (theorem)
8. The number of five digit telephone
numbers having at least one of their digits repeated is
(1) 90000
(2) 10000
(3) 30240
(4)
69760.
Solution

9. If a2-aC2 = a2-a C4
then the value of ’a’ is
(1) 2
(2)
3
(3) 4
(4) 5
Solution
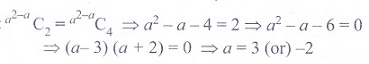
10. There are 10 points in a plane and 4
of them are collinear. The number of straight lines joining any two points is
(1) 45
(2)
40
(3) 39
(4) 38.
Solution
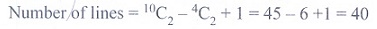
11. The number of ways in which a host
lady invite 8 people for a party of 8 out of 12 people of whom two do not want
to attend the party together is
(1) 2 x11C7 +10C8
(2) 11C7 +10C8
(3)
12C8 -10C6
(4) 10C6 + 2!.
Solution

12. The number of parallelograms that
can be formed from a set of four parallel lines intersecting another set of
three parallel lines.
(1) 6
(2) 9
(3) 12
(4)
18
Solution
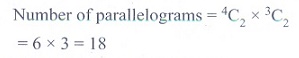
13. Everybody in a room shakes hands
with everybody else. The total number of shake hands is 66. The number of
persons in the room is
(1) 11
(2)
12
(3) 10
(4) 6
Solution

14. Number of sides of a polygon having
44 diagonals is
(1) 4
(2) 4!
(3)
11
(4) 22
Solution
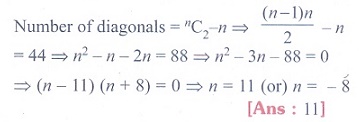
15. If 10 lines are drawn in a plane
such that no two of them are parallel and no three are concurrent, then the
total number of points of intersection are
(1)
45
(2) 40
(3)10!
(4) 210
Solution
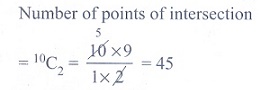
16. In a plane there are 10 points are
there out of which 4 points are collinear, then the number of triangles formed
is
(1) 110
(2) 10C3
(3) 120
(4)
116
Solution
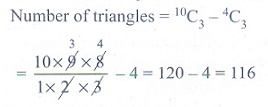
17. In 2nC3 :n
C3 = 11 : 1 then n is
(1) 5
(2)
6
(3)11
(4)7
Solution
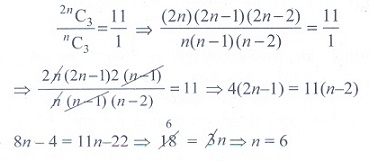
18. (n-1)Cr +(n-1) C(r-1) is
(1) (n+1)Cr
(2) (n-1)Cr
(3)
nCr
(4)nCr-1.
Solution

19. The number of ways of choosing 5
cards out of a deck of 52 cards which include at least one king is
(1) 52C5
(2) 48C5
(3)52C5 +48
C5
(4)52C5
-48 C5.
Solution

20. The number of rectangles that a
chessboard has………..
(1) 81
(2) 99
(3)1296
(4) 6561
Solution

21. The number of 10 digit number that
can be written by using the digits 2 and 3 is
(1) 10C2 + 9C2
(2)
210
(3)210 - 2
(4) 10!
Solution
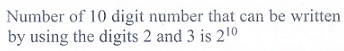
22. If Pr stands for rPr
then the sum of the series 1 + P1 + 2P2 + 3P3
+……….+ nPn is
(1) Pn+1
(2)
Pn+1 - 1
(3) Pn-1 + 1
(4)(n+1)P(n-1)
Solution

23. The product of first n odd natural
numbers equals
(1) 2nCn x nPn
(2)
(1/2 )n x2nCn xn Pn
(3) (1/4 )n x 2nCn
x 2n Pn
(4)nCn x nPn
Solution
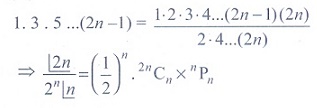
24. If nC4, nC5,
nC6 are in AP the value of n can be
(1)
14
(2) 11
(3)9
(4)5
Solution

25. 1 + 3 + 5 + 7 +……….+ 17 is equal to
(1) 101
(2)
81
(3) 71
(4) 61
Solution
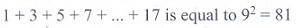
Related Topics